

还剩8页未读,
继续阅读
2021年青岛版六上数学第一单元小手艺展示--分数乘法检测题
展开
这是一份2021年青岛版六上数学第一单元小手艺展示--分数乘法检测题,共1页。
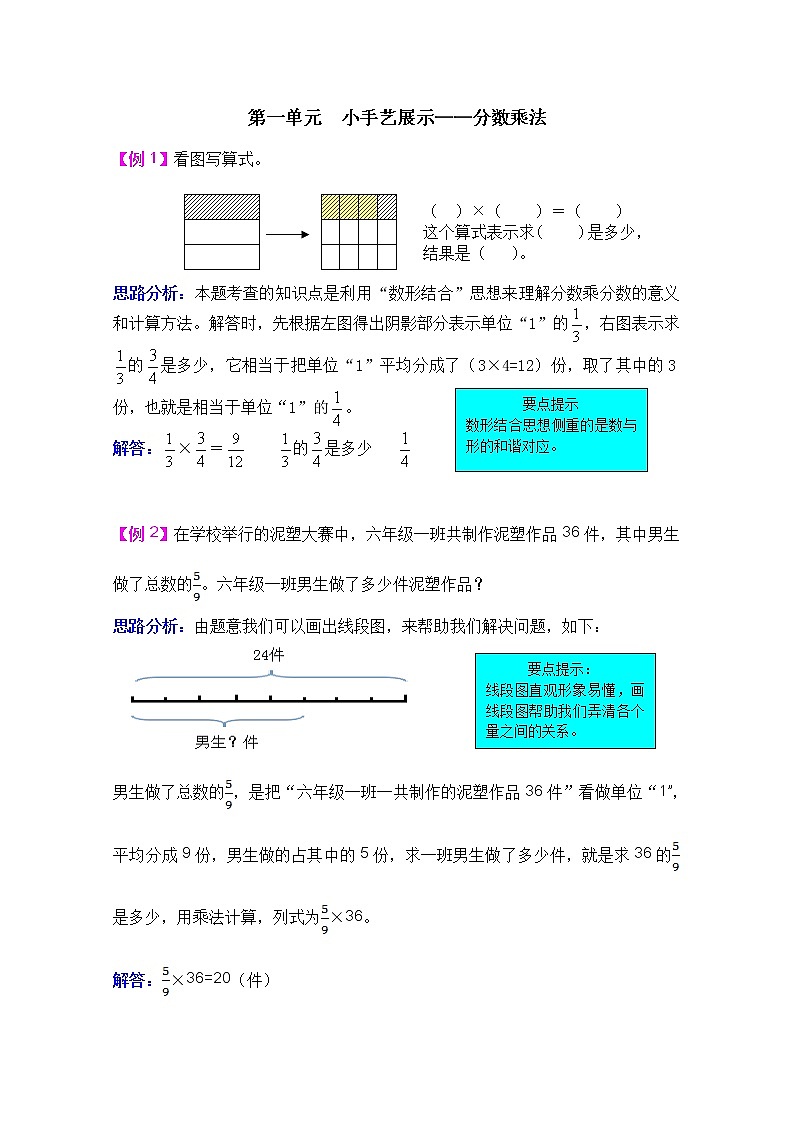
( )×( )=( )
这个算式表示求( )是多少,结果是( )。
要点提示
数形结合思想侧重的是数与形的和谐对应。
思路分析:本题考查的知识点是利用“数形结合”思想来理解分数乘分数的意义和计算方法。解答时,先根据左图得出阴影部分表示单位“1”的,右图表示求的是多少,它相当于把单位“1”平均分成了(3×4=12)份,取了其中的3份,也就是相当于单位“1”的。
解答:×= 的是多少
【例2】在学校举行的泥塑大赛中,六年级一班共制作泥塑作品36件,其中男生做了总数的。六年级一班男生做了多少件泥塑作品?
思路分析:由题意我们可以画出线段图,来帮助我们解决问题,如下:
要点提示:
线段图直观形象易懂,画线段图帮助我们弄清各个量之间的关系。
男生做了总数的,是把“六年级一班一共制作的泥塑作品36件”看做单位“1”,平均分成9份,男生做的占其中的5份,求一班男生做了多少件,就是求36的是多少,用乘法计算,列式为×36。
解答:×36=20(件)
答:六年级一班男生做了20件泥塑作品。
【例3】甲乙两地相距480千米,A、B两列火车同时从两地相对开出,经过3时,A车行了全程的,B车行了全程的。哪列火车离终点近一些?
思路分析:由题意可知,甲乙两地相距480千米,有AB两列火车从两地相对开出,经过3小时,两列火车都行驶了一段距离,问题是让我们判断哪列火车离终点更近一些。我们可以现求出这两列火车分别离终点还有多远,再进行比较。
要点提示:
也可以比较AB两列火车分别行驶的距离,行驶距离越远的离终点更近一些。
A车距离终点:480-480×=180(千米)
B车距离终点:480-480×=192(千米)
180<192 所以A车离终点近一些。
解答:A车距离终点:480-480×=180(千米)
B车距离终点:480-480×=192(千米)
180<192 所以A车离终点近一些。
【例4】看图列式计算。
(1) (2)
思路分析:要点提示:
看懂图意和找准单位“1”是解决此类问题的关键。
(1)看图可知,一台彩电原件2400元,把原价分成6份,现价占其中的5份,要求现价是多少元,是把原价当作单位“1”,用乘法计算,列式为2400×=2000(元)。
(2)看图可知,鸡有480只,把鸡分成6份,鸭占其中的5份,鹅占其中的2份,要求鹅有多少只,是把鸡的只数当作单位“1”,用乘法计算,列式为480×=160(只)。
解答:(1)2400×=2000(元) (2)480×=160(只)
【例5】有甲乙两箱苹果,甲箱里有苹果25千克,拿出它的后,这时两箱苹果的质量相等。乙箱原有苹果多少千克?
要点提示:
明确拿出的部分就是甲比乙多的部分。
思路分析:由题意可知,甲箱里原有25千克苹果,后来拿出了,也就是拿出了25×=5(千克)苹果,这时甲乙两箱苹果就一样多了,说明甲箱苹果比乙箱苹果多的部分刚好和从甲箱中拿出的部分是一样多的,即甲箱苹果比乙箱苹果多5千克。要求乙箱原有多少千克的苹果,就是用甲箱的苹果质量减去多的那部分即可,列式为25-5=20(千克)。
解答:25-25×=20(千克)
答:乙箱原有苹果20千克。
【例6】老妇卖鸡蛋,有趣又大方,见人卖一半,还送半盒蛋,见了4个人,卖光箱中蛋,请问箱中蛋几盒?
要点提示
逆推法解题也就是由结果出发,逐步还原至最初。
思路分析:本题考查的知识点是用“逆推法”来解答分数乘法问题。解答时,先从遇到最后一个人,卖了一半,送了半盒,刚好卖完,分析得出,最后一个人得到的是:×2=1(盒)蛋;遇到第三个人,卖了一半,送了半盒,这时有:(1+)×2=3(盒);遇到第二个人,卖了一半,送了半盒,这时有:(3+)×2=7(盒);遇到第一个人,卖了一半,送了半盒,一共有:(7+)×2=15(盒)。
解答:×2=1(盒) (1+)×2=3(盒)
(3+)×2=7(盒) (7+)×2=15(盒)
答:箱中有鸡蛋15盒。
要点提示:
可先动手实际操作一下,看看对折三次后是几段。
【例7】把一根绳子对折三次后长米,这根绳子一共有多长?
思路分析:我们先折一折。如下图所示,图一表示对折一次后一根绳子变成了两段,图二表示再对折一次(对折两次)后变成了四段,图三表示再对折一次(对折三次)后变成了八段。
题中要求这根绳子一共有多长,就是求对折三次后的八段共有多长,由题干已知对折三次后每段长米,所以将这八段绳子的长度加起来就是这根绳子的总长度,用加法或乘法计算,列乘法算式为×8=(米)。
解答:×8=(米)
答:这根绳子一共长米。
【例8】六年级一班有48人,在第一单元测评中,成绩优秀的学生人数占全班人数的,不及格人数是成绩优秀学生人数的。这次考试中及格以上的有多少人?
思路分析:由题意可知,六年级一班有48人,在第一单元测评中,既有成绩优秀的学生,也有成绩及格和不及格的学生,要求在此次考试中几个以上的人数,就是用全班总人数减去不及格人数,但是题目中并未直接给出不及格的人数,所以我们要先求出不及格的人数。我们可以通过成绩优秀的学人数求出不及格的人数。
要点提示:
找准单位“1”是解决此类问题的关键。
成绩优秀的学生人数:48×=28(人)
成绩不及格的学生人数:28×=4(人)
用全班总人数减去不及格人数即可求出及格以上的学生人数。
解答:成绩优秀的学生人数:48×=28(人)
成绩不及格的学生人数:28×=4(人)
成绩及格以上人数:48-4=44(人)
答:这次考试中及格以上的有44人。
【例9】一位老人养了17只羊,临终前立下遗嘱:大儿子分,二儿子分,三儿子分,并且分羊时不许宰杀。老人临终后,三个儿子犯了愁,这怎么分呢?亲爱的同学,你能帮帮他们吗?
要点提示
借数法是常用的解决问题的方法。
思路分析:本题考查的知识点是通过“借数法”来解答分数乘法简单的实际问题。解答时,我们会发现已知信息中,单位“1”的、和都不是整数只,但++=,所以先借1只羊,这样变成18只,通过计算18的、和来求解。
解答:先借一只羊 17+1=18(只)
18×=9(只) 18×=6(只) 18×=2(只) 9+6+2=17(只)
答:老大分9只,老二分6只,老三分2只。
【例10】计算+++…+。
思路分析:这是一道考查分数的乘法和加法题,初看此题很多人会拿起笔就直接一个一个计算,然后再加起来,这样做不但繁琐,而且容易出错,那到底有没有更简便的方法呢?答案是肯定的。
要点提示:
转化法是常用的数学方法之一。
先看第一个分数:=×==-
再看第二个分数:=×==-
再看第三个分数:=×==-
……
依此类推,我们发现原来的算式可以转化成减法算式,如下:
+++…+=-+-+-+…+-=-=
解答:+++…+
=-+-+-+…+-
=-
=
【例11】2017减去它的,再减去余下的、又减去余下的、以后每次都减去余下的、……依此类推,一直减到最后余下的,那么最后得多少?
思路分析:本题考查的知识点是用类推法解答“连续余问题”,解答时,先从2017减去它的开始分析,还剩下2017×(1-),再减去余下的,还剩下余下的(1-),即2017×(1-)×(1-),依次类推,一直减到最后余下的,最后剩下的是2017×(1-)×(1-)×(1-)×……×(1-),然后找规律计算出结果即可。
解答:2017×(1-)×(1-)×(1-)×……×(1-)
=2017××××……×
=2017×
=1
【例12】一个长方体的水箱,从里面量长是米,宽是米,高是米,这个长方体水箱的容积是多少?
要点提示:
长方体的容积=长×宽× 高。
思路分析:由题意可知,这个水箱的形状是一个长方体,而且给出了从里面量得的长、宽、高的具体数值。要求这个水箱的容积,可以根据长方体的体积公式解答,列式为。计算时,能约的要先约分,使计算更加简便。
解答:=(立方米)
答:这个长方体水箱的容积是立方米。
【例13】“双十一”购物节活动中,两家商铺都在搞促销活动,洗衣液原价每瓶30元,甲店买五送一,乙店按原价的出售,李阿姨要买12瓶洗衣液,到哪家商店购买更合算?
思路分析:要想得出到哪家商店购买更合算,就要分别求出在两个商店购买12瓶洗衣液所花的钱数,甲店买五送一,也就是用原来5瓶的钱,现在可以得到6瓶,也就是每6瓶中有5瓶是买的,1瓶是送的。要看12瓶中有几个6瓶,列式为12÷6=2个,买12瓶花的钱数就是2个5瓶的钱数,也就是10瓶的钱数;乙店按原价的出售,只要计算出12瓶洗衣液原价的是多少即可,然后进行对比即可得出答案。
要点提示:
本题也可以先求出甲店买五送一后每瓶洗衣液的单价,再根据数量求出总价。
解答:甲店:12÷6=2(个) 5×2×30=300(元)
乙店:12×30×=288(元)
288<300
答:到乙店购买更合算。
【例14】有两堆同样多的煤,第1堆运走吨,第2堆运走,两堆煤剩下的部分同样重吗?为什么?
要点提示:
假设法和列举法都是解决数学问题的常用方法。
思路分析:由于两堆煤的质量不确定,我们可以先假设这两堆煤都是1吨、超过1吨、低于1吨三种情况,计算出第二堆运走的质量,再与第一堆比较。
解答:无法确定那堆稻谷剩下的质量多。
【例15】a,b是不为0的自然数,已知a×<a,a×>a,求b的值。
要点提示:
明确积与因数的大小关系是解决本题的关键。
思路分析:由“一个不为0的数乘小于1的数,得数小于它本身”,可知“a×<a”中的小于1,所以b<8。
由“一个不为0的数乘大于1的数,得数大于它本身”,可知“a×>a”中的大于1,所以b>6。
因为b是不为0的自然数,且6<b<8,所以b=7。
解答:b=7
【例16】已知a、b和c都是不为0的整数,如果×a=×b=×c,那么a、b和c,哪个数最大?哪个数最小?
思路分析:题中要比较a、b、c谁最大谁最小,我们有两种方法:
方法一:假设法。
要点提示:
假设法是解决数学问题的常用方法之一。
假设×a=×b=×c=1,那么a=,b=,c=,接下来直接利用异分母分数比较大小的方法进行比较,可知c最大,a最小。
方法二:直接比较法(乘法算式中因数与因数之间的关系)。
已知×a=×b=×c,那么我们可以先比较、、这三个因数的大小,可知>,然后根据乘法算式中因数之间的关系(积不变,一个因数增加或缩小,另一个因数会随之缩小或增大),可知a<b<c,即c最大,a最小。
解答:c最大,a最小。
【例17】对错我来判。(对的打“∨”,错的打上“×”)
(1)因为+=1,所以的倒数是。( )
(2)一个数的倒数一定比这个数小。( )
(3)是倒数,也是倒数。( )
思路分析:本题考查的知识点是倒数的意义。解答时,要明确的是乘积是1的两个数叫做互为倒数,也就是说倒数不是单独存在的,是指两个数的积是1时,我们说其中的一个数是另一个数的倒数。
(1)因为+=1,它们的积×=≠1,所以和不是互为倒数。
要点提示
单独的一个数不能说是倒数。
(2)一个非0自然数的倒数比这个数小,如2的倒数是,但是一个数的倒数不一定比这个数小,如的倒数是3,3就比大。
(3)互为倒数的两个数的积是1,也就是说乘积
是1的两个数互为倒数,单独的一个数不能说倒
数,所以是倒数,也是倒数都是错误的。
解答:(1)× (2)× (3)×
【例18】一个自然数与它的倒数的差是21,这个自然数是多少?
思路分析:本题考查的知识点是运用转化法解答倒数差问题。解答时,先把21转化为21+,它等于22-的差,22和互为倒数,21正好是22与的差,所以得出这个数是22。
解答:22
( )×( )=( )
这个算式表示求( )是多少,结果是( )。
要点提示
数形结合思想侧重的是数与形的和谐对应。
思路分析:本题考查的知识点是利用“数形结合”思想来理解分数乘分数的意义和计算方法。解答时,先根据左图得出阴影部分表示单位“1”的,右图表示求的是多少,它相当于把单位“1”平均分成了(3×4=12)份,取了其中的3份,也就是相当于单位“1”的。
解答:×= 的是多少
【例2】在学校举行的泥塑大赛中,六年级一班共制作泥塑作品36件,其中男生做了总数的。六年级一班男生做了多少件泥塑作品?
思路分析:由题意我们可以画出线段图,来帮助我们解决问题,如下:
要点提示:
线段图直观形象易懂,画线段图帮助我们弄清各个量之间的关系。
男生做了总数的,是把“六年级一班一共制作的泥塑作品36件”看做单位“1”,平均分成9份,男生做的占其中的5份,求一班男生做了多少件,就是求36的是多少,用乘法计算,列式为×36。
解答:×36=20(件)
答:六年级一班男生做了20件泥塑作品。
【例3】甲乙两地相距480千米,A、B两列火车同时从两地相对开出,经过3时,A车行了全程的,B车行了全程的。哪列火车离终点近一些?
思路分析:由题意可知,甲乙两地相距480千米,有AB两列火车从两地相对开出,经过3小时,两列火车都行驶了一段距离,问题是让我们判断哪列火车离终点更近一些。我们可以现求出这两列火车分别离终点还有多远,再进行比较。
要点提示:
也可以比较AB两列火车分别行驶的距离,行驶距离越远的离终点更近一些。
A车距离终点:480-480×=180(千米)
B车距离终点:480-480×=192(千米)
180<192 所以A车离终点近一些。
解答:A车距离终点:480-480×=180(千米)
B车距离终点:480-480×=192(千米)
180<192 所以A车离终点近一些。
【例4】看图列式计算。
(1) (2)
思路分析:要点提示:
看懂图意和找准单位“1”是解决此类问题的关键。
(1)看图可知,一台彩电原件2400元,把原价分成6份,现价占其中的5份,要求现价是多少元,是把原价当作单位“1”,用乘法计算,列式为2400×=2000(元)。
(2)看图可知,鸡有480只,把鸡分成6份,鸭占其中的5份,鹅占其中的2份,要求鹅有多少只,是把鸡的只数当作单位“1”,用乘法计算,列式为480×=160(只)。
解答:(1)2400×=2000(元) (2)480×=160(只)
【例5】有甲乙两箱苹果,甲箱里有苹果25千克,拿出它的后,这时两箱苹果的质量相等。乙箱原有苹果多少千克?
要点提示:
明确拿出的部分就是甲比乙多的部分。
思路分析:由题意可知,甲箱里原有25千克苹果,后来拿出了,也就是拿出了25×=5(千克)苹果,这时甲乙两箱苹果就一样多了,说明甲箱苹果比乙箱苹果多的部分刚好和从甲箱中拿出的部分是一样多的,即甲箱苹果比乙箱苹果多5千克。要求乙箱原有多少千克的苹果,就是用甲箱的苹果质量减去多的那部分即可,列式为25-5=20(千克)。
解答:25-25×=20(千克)
答:乙箱原有苹果20千克。
【例6】老妇卖鸡蛋,有趣又大方,见人卖一半,还送半盒蛋,见了4个人,卖光箱中蛋,请问箱中蛋几盒?
要点提示
逆推法解题也就是由结果出发,逐步还原至最初。
思路分析:本题考查的知识点是用“逆推法”来解答分数乘法问题。解答时,先从遇到最后一个人,卖了一半,送了半盒,刚好卖完,分析得出,最后一个人得到的是:×2=1(盒)蛋;遇到第三个人,卖了一半,送了半盒,这时有:(1+)×2=3(盒);遇到第二个人,卖了一半,送了半盒,这时有:(3+)×2=7(盒);遇到第一个人,卖了一半,送了半盒,一共有:(7+)×2=15(盒)。
解答:×2=1(盒) (1+)×2=3(盒)
(3+)×2=7(盒) (7+)×2=15(盒)
答:箱中有鸡蛋15盒。
要点提示:
可先动手实际操作一下,看看对折三次后是几段。
【例7】把一根绳子对折三次后长米,这根绳子一共有多长?
思路分析:我们先折一折。如下图所示,图一表示对折一次后一根绳子变成了两段,图二表示再对折一次(对折两次)后变成了四段,图三表示再对折一次(对折三次)后变成了八段。
题中要求这根绳子一共有多长,就是求对折三次后的八段共有多长,由题干已知对折三次后每段长米,所以将这八段绳子的长度加起来就是这根绳子的总长度,用加法或乘法计算,列乘法算式为×8=(米)。
解答:×8=(米)
答:这根绳子一共长米。
【例8】六年级一班有48人,在第一单元测评中,成绩优秀的学生人数占全班人数的,不及格人数是成绩优秀学生人数的。这次考试中及格以上的有多少人?
思路分析:由题意可知,六年级一班有48人,在第一单元测评中,既有成绩优秀的学生,也有成绩及格和不及格的学生,要求在此次考试中几个以上的人数,就是用全班总人数减去不及格人数,但是题目中并未直接给出不及格的人数,所以我们要先求出不及格的人数。我们可以通过成绩优秀的学人数求出不及格的人数。
要点提示:
找准单位“1”是解决此类问题的关键。
成绩优秀的学生人数:48×=28(人)
成绩不及格的学生人数:28×=4(人)
用全班总人数减去不及格人数即可求出及格以上的学生人数。
解答:成绩优秀的学生人数:48×=28(人)
成绩不及格的学生人数:28×=4(人)
成绩及格以上人数:48-4=44(人)
答:这次考试中及格以上的有44人。
【例9】一位老人养了17只羊,临终前立下遗嘱:大儿子分,二儿子分,三儿子分,并且分羊时不许宰杀。老人临终后,三个儿子犯了愁,这怎么分呢?亲爱的同学,你能帮帮他们吗?
要点提示
借数法是常用的解决问题的方法。
思路分析:本题考查的知识点是通过“借数法”来解答分数乘法简单的实际问题。解答时,我们会发现已知信息中,单位“1”的、和都不是整数只,但++=,所以先借1只羊,这样变成18只,通过计算18的、和来求解。
解答:先借一只羊 17+1=18(只)
18×=9(只) 18×=6(只) 18×=2(只) 9+6+2=17(只)
答:老大分9只,老二分6只,老三分2只。
【例10】计算+++…+。
思路分析:这是一道考查分数的乘法和加法题,初看此题很多人会拿起笔就直接一个一个计算,然后再加起来,这样做不但繁琐,而且容易出错,那到底有没有更简便的方法呢?答案是肯定的。
要点提示:
转化法是常用的数学方法之一。
先看第一个分数:=×==-
再看第二个分数:=×==-
再看第三个分数:=×==-
……
依此类推,我们发现原来的算式可以转化成减法算式,如下:
+++…+=-+-+-+…+-=-=
解答:+++…+
=-+-+-+…+-
=-
=
【例11】2017减去它的,再减去余下的、又减去余下的、以后每次都减去余下的、……依此类推,一直减到最后余下的,那么最后得多少?
思路分析:本题考查的知识点是用类推法解答“连续余问题”,解答时,先从2017减去它的开始分析,还剩下2017×(1-),再减去余下的,还剩下余下的(1-),即2017×(1-)×(1-),依次类推,一直减到最后余下的,最后剩下的是2017×(1-)×(1-)×(1-)×……×(1-),然后找规律计算出结果即可。
解答:2017×(1-)×(1-)×(1-)×……×(1-)
=2017××××……×
=2017×
=1
【例12】一个长方体的水箱,从里面量长是米,宽是米,高是米,这个长方体水箱的容积是多少?
要点提示:
长方体的容积=长×宽× 高。
思路分析:由题意可知,这个水箱的形状是一个长方体,而且给出了从里面量得的长、宽、高的具体数值。要求这个水箱的容积,可以根据长方体的体积公式解答,列式为。计算时,能约的要先约分,使计算更加简便。
解答:=(立方米)
答:这个长方体水箱的容积是立方米。
【例13】“双十一”购物节活动中,两家商铺都在搞促销活动,洗衣液原价每瓶30元,甲店买五送一,乙店按原价的出售,李阿姨要买12瓶洗衣液,到哪家商店购买更合算?
思路分析:要想得出到哪家商店购买更合算,就要分别求出在两个商店购买12瓶洗衣液所花的钱数,甲店买五送一,也就是用原来5瓶的钱,现在可以得到6瓶,也就是每6瓶中有5瓶是买的,1瓶是送的。要看12瓶中有几个6瓶,列式为12÷6=2个,买12瓶花的钱数就是2个5瓶的钱数,也就是10瓶的钱数;乙店按原价的出售,只要计算出12瓶洗衣液原价的是多少即可,然后进行对比即可得出答案。
要点提示:
本题也可以先求出甲店买五送一后每瓶洗衣液的单价,再根据数量求出总价。
解答:甲店:12÷6=2(个) 5×2×30=300(元)
乙店:12×30×=288(元)
288<300
答:到乙店购买更合算。
【例14】有两堆同样多的煤,第1堆运走吨,第2堆运走,两堆煤剩下的部分同样重吗?为什么?
要点提示:
假设法和列举法都是解决数学问题的常用方法。
思路分析:由于两堆煤的质量不确定,我们可以先假设这两堆煤都是1吨、超过1吨、低于1吨三种情况,计算出第二堆运走的质量,再与第一堆比较。
解答:无法确定那堆稻谷剩下的质量多。
【例15】a,b是不为0的自然数,已知a×<a,a×>a,求b的值。
要点提示:
明确积与因数的大小关系是解决本题的关键。
思路分析:由“一个不为0的数乘小于1的数,得数小于它本身”,可知“a×<a”中的小于1,所以b<8。
由“一个不为0的数乘大于1的数,得数大于它本身”,可知“a×>a”中的大于1,所以b>6。
因为b是不为0的自然数,且6<b<8,所以b=7。
解答:b=7
【例16】已知a、b和c都是不为0的整数,如果×a=×b=×c,那么a、b和c,哪个数最大?哪个数最小?
思路分析:题中要比较a、b、c谁最大谁最小,我们有两种方法:
方法一:假设法。
要点提示:
假设法是解决数学问题的常用方法之一。
假设×a=×b=×c=1,那么a=,b=,c=,接下来直接利用异分母分数比较大小的方法进行比较,可知c最大,a最小。
方法二:直接比较法(乘法算式中因数与因数之间的关系)。
已知×a=×b=×c,那么我们可以先比较、、这三个因数的大小,可知>,然后根据乘法算式中因数之间的关系(积不变,一个因数增加或缩小,另一个因数会随之缩小或增大),可知a<b<c,即c最大,a最小。
解答:c最大,a最小。
【例17】对错我来判。(对的打“∨”,错的打上“×”)
(1)因为+=1,所以的倒数是。( )
(2)一个数的倒数一定比这个数小。( )
(3)是倒数,也是倒数。( )
思路分析:本题考查的知识点是倒数的意义。解答时,要明确的是乘积是1的两个数叫做互为倒数,也就是说倒数不是单独存在的,是指两个数的积是1时,我们说其中的一个数是另一个数的倒数。
(1)因为+=1,它们的积×=≠1,所以和不是互为倒数。
要点提示
单独的一个数不能说是倒数。
(2)一个非0自然数的倒数比这个数小,如2的倒数是,但是一个数的倒数不一定比这个数小,如的倒数是3,3就比大。
(3)互为倒数的两个数的积是1,也就是说乘积
是1的两个数互为倒数,单独的一个数不能说倒
数,所以是倒数,也是倒数都是错误的。
解答:(1)× (2)× (3)×
【例18】一个自然数与它的倒数的差是21,这个自然数是多少?
思路分析:本题考查的知识点是运用转化法解答倒数差问题。解答时,先把21转化为21+,它等于22-的差,22和互为倒数,21正好是22与的差,所以得出这个数是22。
解答:22

相关资料
更多









