高中数学北师大版 (2019)选择性必修 第二册2.2 等差数列的前n项和示范课课件ppt

这是一份高中数学北师大版 (2019)选择性必修 第二册2.2 等差数列的前n项和示范课课件ppt，共49页。PPT课件主要包含了复习回顾，想一想，试一试，议一议，Sn的深入认识，等差数列的主要性质等内容，欢迎下载使用。

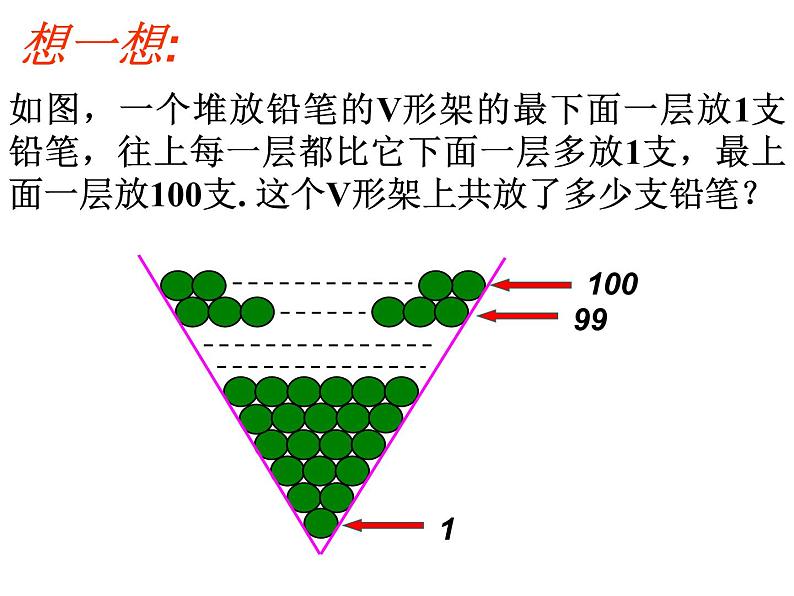
如图，一个堆放铅笔的V形架的最下面一层放1支铅笔，往上每一层都比它下面一层多放1支，最上面一层放100支. 这个V形架上共放了多少支铅笔？
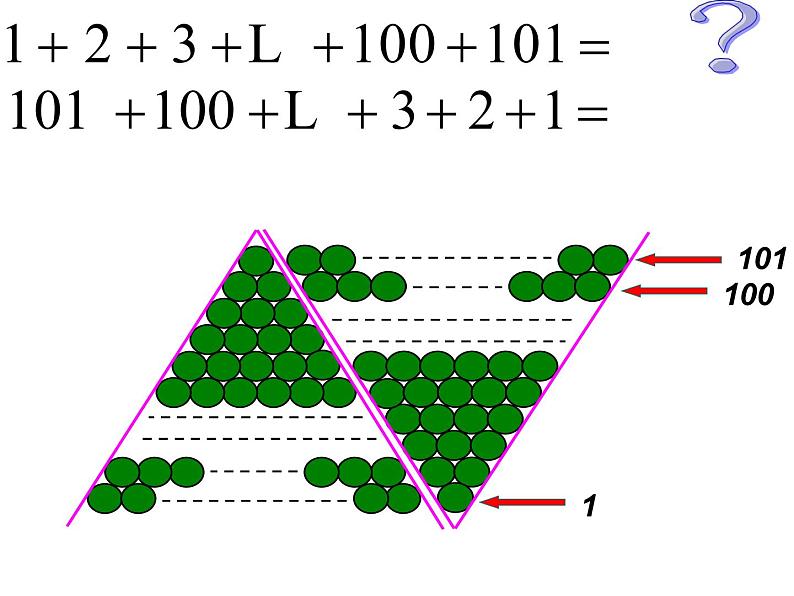
1+1002+99. . .50+51

一、数列前n项和的意义
数列｛an｝：a1，a2 ,a3 ，…，an ,…
我们把a1＋a2 ＋ a3 ＋ … ＋ an叫做数列｛an｝的前n项和，记作Sn
二、等差数列的前n项和公式推导
我国数列求和的概念起源很早，到南北朝时，张丘建始创等差数列求和解法。他在《张丘建算经》中给出等差数列求和问题：例如：今有女子不善织布，每天所织的布以同数递减，初日织五尺，
末一日织一尺，共织三十日，问共织几何？
原书的解法是：“并初、末日织布数，半之
1.根据下列各题中的条件,求相应的等差数列｛an｝的前n项和Sn
例1：等差数列－10，－6，－2，2，·······前多少项和是54 ？
解: 设题中的等差数列为{an}, 则 a1= -10 d= -6-(-10)=4. 设 Sn= 54,
得     n2-6n-27=0        得 n1=9, n2=-3(舍去）。       因此等差数列 －10，－6，－2，2， ······· 前9项和是54。
例2．等差数列 中， 求 的值。
解：由 得：
在等差数列 {an} 中，如果已知五个元素 a1, an, n, d, Sn 中的任意三个, 请问: 能否求出其余两个量 ?
等差数列{an}的首项为a1，公差为d，项数为n，第n项为an，前n项和为Sn，请填写下表：
1.等差数列前n项和Sn公式的推导: 倒序相加法2.等差数列前n项和Sn公式的记忆与应用；
说明：(1)正确合理的选择公式. (2)注意与通项公式相结合.
例3、已知一个等差数列｛an｝的前10项的和是310，前20项的和是1220，由这些条件能确定这个等差数列的前n项和的公式吗？
分析：方程思想和前n项和公式相结合
解：由题意知：S10＝310，S20＝1220，将它们代入公式
例3变式、已知一个等差数列｛an｝的前10项的和是310，前20项的和是1220，由这些条件能确定这个等差数列的前30项和的公式吗？
【另解】由等差数列的性质，可推得：
解得：前30项的和为2730 .
上述方法没有列出方程求出具体的个别量，而是恰当地运用数学中的整体思想来快速求出，要注意体会这种思想在数学中的运用.
在等差数列{an}中，Sn，S2n- Sn ，S3n-S2n…构成一个怎样的数列？
等差数列{an}中, S4=1,S8=4, 求 a9+a10+a11+a12=
当n >1时： ①
当n >1时： ①
● 如果一个数列 的前n项和为其中p、q、r为常数，且p≠0，那么这个数列一定是等差数列吗？如果是，它的首项和公差是什么？
（1）若r≠0，则这个数列一定不是等差数列.（2）若r＝0，则这个数列一定是等差数列.
结论：数列是等差数列等价于
将等差数列前n项和公式 看作是一个关于n的函数，这个函数 有什么特点？
当d≠0时,Sn是常数项为零的二次函数
则 Sn=An2+Bn
思考：当首项、公差确定时，Sn的结构有什么特征？
2.当d不为0时，点（n,Sn)是在常数项为0的一个二次函数的图象上。
结论1：{an}为等差数列 ，这是一个关于 的 没有 的“ ”
（ 注意 a 还可以是 0）
有最大值(至于是否在顶点处取得,要看顶点处所对应的横坐标距离它最近的正整数处取得,一般情况下或一,或两个最值),如右图所示:
2.当公差d>0即a>0时,
3.当公差d =0即a=0时,
1.当公差d <0即a<0时,
,则它是关于n的一次函数,
等差数列的前n项和例题4
变式.等差数列{an}中，已知an=2(n-12)，求此数列前n项和的最小值。
归纳：(1)当a1>0,d>0时,Sn有最小值无最大值，且最小值为S1； (2)当a1>0,d<0时,Sn有最大值无最小值，当am≥0且am+1≤0,Sn的最大值为Sm； (3)当a1<0,d>0时,Sn有最小值无最大值，当am≤0且am+1≥0,Sn的最小值为Sm； (4)当a1<0,d<0时,Sn有最大值无最小值，且最大值为S1。
　练习3：　等差数列－10，－6，－2，2，…的前多少项的和最小？
7、等差数列前n项和的最值问题有两种方法：
(1) 当an＞0，d＜0，前n项和有最大值. 可由an≥0，且an＋1 ≤0，求得n的值；
当an＜0，d＞0，前n项和有最小值. 可由an≤0，且an＋1≥0，求得n的值.
Sn = 2n2-12n
等差数列的前n项的最值问题
例1.已知等差数列{an}中,a1=13且S3=S11,求n取何值时,Sn取最大值.
∴当n=7时,Sn取最大值49.
∴ an=13+(n-1) ×(-2)=－2n+15
例2 设等差数列{an}、{bn}的前n项 和分别为Sn、Tn，若 ， 求 的值.
设等差数列{an}、{bn}的前n项和 分别为Sn、Tn，则 等于什么？
1.等差数列的定义特征
从第2项起，每一项与它的前一项的差等于同一个常数.
或an－1＋an＋1＝2 an(n≥2).
2.等差数列的递推公式
an－an－1 ＝d (n≥2).
3.等差数列的通项公式
an＝a1＋(n－1)d＝am＋(n－m)d＝pn＋q.
4.等差数列的前n项和公式
S3n＝3(S2n－Sn)
（6）若数列{an}、{bn}都是等差数列，则数列{pan+q}，{an＋an＋1}，{xan＋ybn}，也是等差数列.
(7) m＋n＝p＋q  am＋an＝ap＋aq.
等差数列的性质应用：
例3、已知一个等差数列的总项数为奇数， 且奇数项之和为77，偶数项之和为 66，求中间项及总项数。