

2021学年22.1.2 二次函数y=ax2的图象和性质课后测评
展开专题16 二次函数y=ax^2的图象和性质
班级_________ 姓名_________ 学号_________ 分数_________
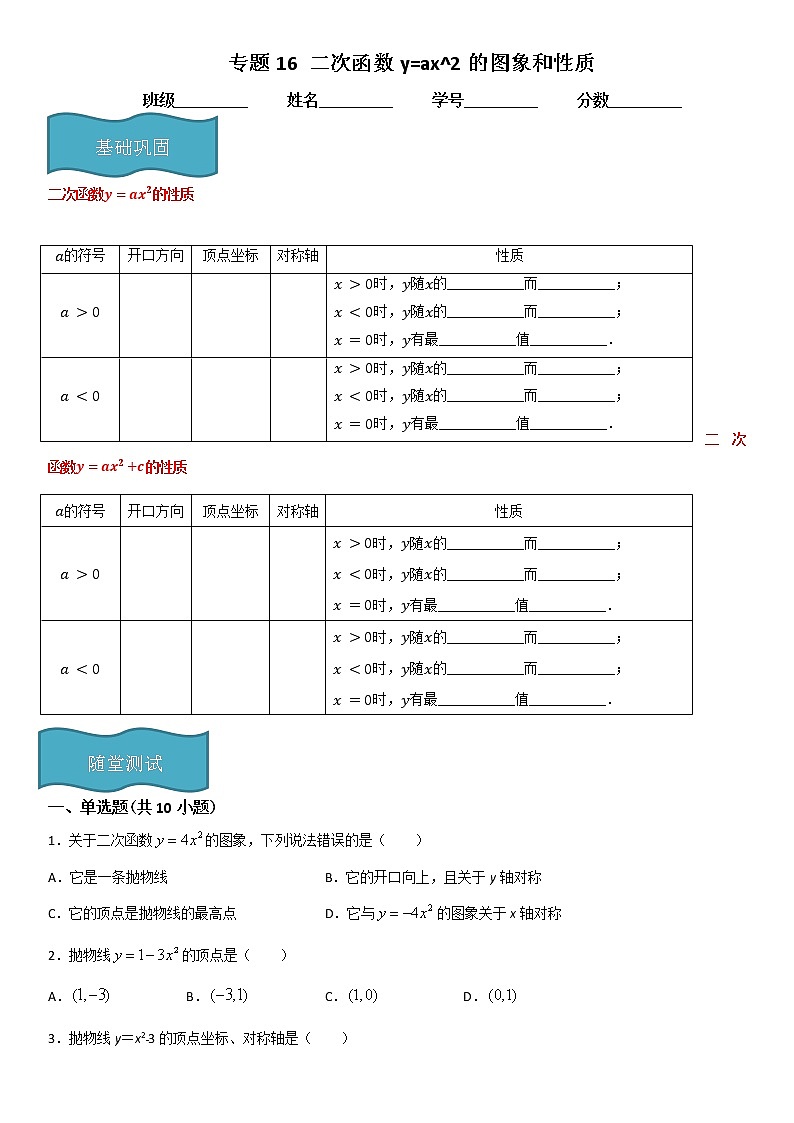
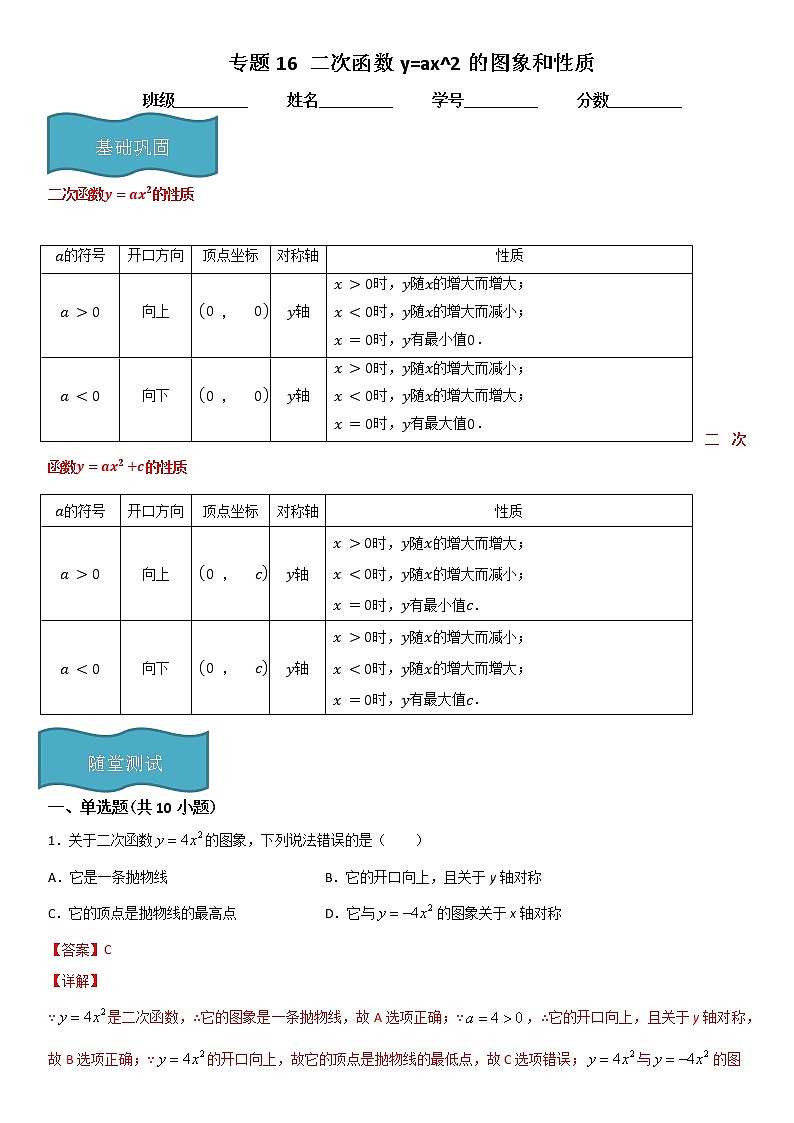
二次函数的性质
的符号 | 开口方向 | 顶点坐标 | 对称轴 | 性质 |
|
|
| 时,随的___________而___________; 时,随的___________而___________; 时,有最___________值___________. | |
|
|
| 时,随的___________而___________; 时,随的___________而___________; 时,有最___________值___________. |
二次函数的性质
的符号 | 开口方向 | 顶点坐标 | 对称轴 | 性质 |
|
|
| 时,随的___________而___________; 时,随的___________而___________; 时,有最___________值___________. | |
|
|
| 时,随的___________而___________; 时,随的___________而___________; 时,有最___________值___________. |
一、单选题(共10小题)
1.关于二次函数的图象,下列说法错误的是( )
A.它是一条抛物线 B.它的开口向上,且关于y轴对称
C.它的顶点是抛物线的最高点 D.它与的图象关于x轴对称
2.抛物线的顶点是( )
A. B. C. D.
3.抛物线y=x2﹣3的顶点坐标、对称轴是( )
A.(0,3),x=3 B.(0,﹣3),x=0 C.(3,0),x=3 D.(3,0),x=0
4.下列对二次函数的图象的描述,正确的是( )
A.开口向下 B.对称轴是y轴
C.经过原点 D.在对称轴右侧,抛物线从左到右下降
5.下列关于二次函数的图象与性质的描述,错误的是( )
A.该函数图象的开口向上 B.该函数图象可由函数的图象平移得到
C.该函数图象关于y轴对称 D.函数值y随着自变量x的值的增大而增大
6.若二次函数的图象过点,则必在该图象上的点还有( )
A. B. C. D.
7.已知二次函数y=(m+2),当x<0时,y随x的增大而增大,则m的值为( )
A. B. C. D.2
8.二次函数在内的最小值是( )
A.3 B.2 C.-29 D.-30
9.若抛物线的图象经过点,则它一定会经过( )
A. B. C. D.
10.已知抛物线y=-x2+1,下列结论:
①抛物线开口向上;
②抛物线与x轴交于点(-1,0)和点(1,0);
③抛物线的对称轴是y轴;
④抛物线的顶点坐标是(0,1);
⑤抛物线y=-x2+1是由抛物线y=-x2向上平移1个单位得到的.
其中正确的个数有( )
A.5个 B.4个 C.3个
D.2个
二、填空题(共5小题)
11.如图所示四个二次函数的图象中,分别对应的是①y=ax2;②y=bx2;③y=cx2;④y=dx2.则a、b、c、d的大小关系为_____.
12.已知二次函数y=x2,当x>0时,y随x的增大而_____(填“增大”或“减小”).
13.如果抛物线y=(m﹣1)x2有最低点,那么m的取值范围为_____.
14.若函数y=3x2的图象与直线y=kx+3的交点为(2,b),则k=_____,b=______.
15.若抛物线y=ax2经过点A (,-9),则其解析式为_______________.
三、解答题(共2小题)
16.已知是关于x的二次函数.
(1)求满足条件的k的值;
(2)k为何值时,抛物线有最低点?求出这个最低点.当x为何值时,y的值随x值的增大而增大?
(3)k为何值时,函数有最大值?最大值是多少?当x为何值时,y的值随x值的增大而减小?
17.求符合下列条件的抛物线的表达式.
(1)与的开口大小相同,方向相反;
(2)经过点(-3,2).
初中数学人教版九年级上册22.1.1 二次函数练习题: 这是一份初中数学人教版九年级上册22.1.1 二次函数练习题,共3页。试卷主要包含了填空等内容,欢迎下载使用。
初中数学人教版九年级上册22.1.3 二次函数y=a(x-h)2+k的图象和性质随堂练习题: 这是一份初中数学人教版九年级上册22.1.3 二次函数y=a(x-h)2+k的图象和性质随堂练习题,文件包含专题17二次函数yax-h2+k的图象和性质原卷版docx、专题17二次函数yax-h2+k的图象和性质解析版docx等2份试卷配套教学资源,其中试卷共14页, 欢迎下载使用。
人教版九年级上册22.1.4 二次函数y=ax2+bx+c的图象和性质课后测评: 这是一份人教版九年级上册22.1.4 二次函数y=ax2+bx+c的图象和性质课后测评,文件包含专题18二次函数yax2+bx+c的图象和性质原卷版docx、专题18二次函数yax2+bx+c的图象和性质解析版docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。













