人教A版 (2019)必修 第二册9.2 用样本估计总体图片课件ppt

这是一份人教A版 (2019)必修 第二册9.2 用样本估计总体图片课件ppt，共28页。PPT课件主要包含了温故知新，频率分布直方图的性质，问题探究，概念解析，概念辨析，概念拓展，典例解析，跟踪训练，当堂达标等内容，欢迎下载使用。

1.如何画频率分布直方图的步骤
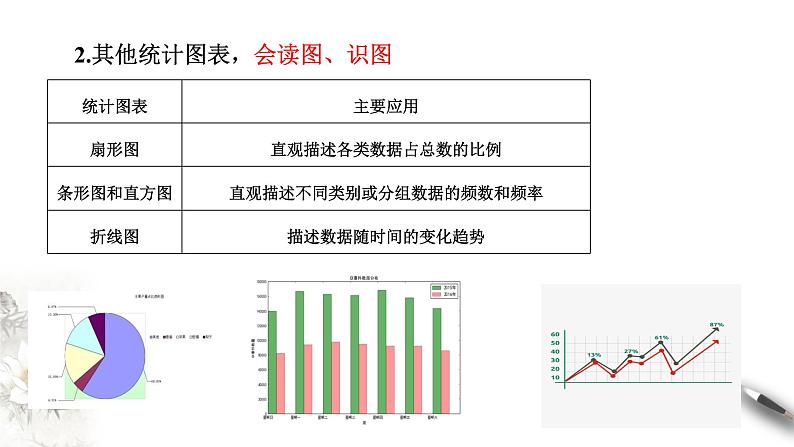
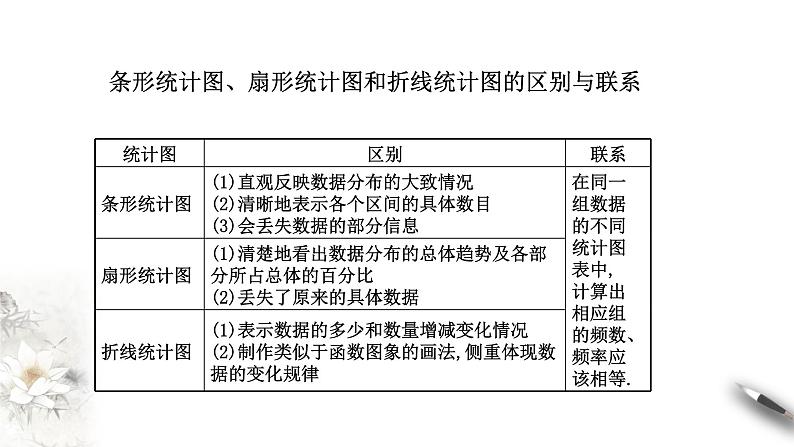
2.其他统计图表，会读图、识图
条形统计图、扇形统计图和折线统计图的区别与联系
前面我们用频率分布表、频率分布直方图描述了居民用户月均用水量的样本数据，通过对图表的观察与分析，得出了一些样本数据的频率分布规律，并由此推测了该市全体居民用户月均用水量的分布情况，得出了“大部分居民用户的月均用水量集中在一个较低值区域”等推断，接下来的问题是，如何利用这些信息，为政府决策服务呢？下面我们对此进行讨论.
问题: 如果该市政府希望使80%的居民用户生活用水费支出不受影响，根据9.2.1节中100户居民用户的月均用水量数据，你能给市政府提出确定居民用户月均用水量标准的建议吗？
根据市政府的要求确定居民用户月均用水量标准，就是要寻找一个数a,使全市居民用户月均用水量中不超过a的占80%,大于a的占20%.
把得到的100个样本数据按从小到大排序，得到第80个和81个数据分别为13.6和13.8.可以发现，区间（13.6,13.8)内的任意一个数，都能把样本数据分成符合要求的两部分.一般地，我们取这两个数的平均数()13.6+13.8)/2=13.7,并称此数为这组数据的第80百分位数（percentile), 或80%分位数.
根据样本数据的第80百分位数，我们可以估计总体数据的第80百分位数为13.7左右.由于样本的取值规律与总体的取值规律之间会存在偏差，而在决策问题中，只要临界值近似为第80百分位数即可，因此为了实际中操作的方便，可以建议市政府把月均用水量标准定为14t,或者把年用水量标准定为168t.
你认为14t这个标准一定能够保证80%的居民用水不超标吗？如果不一定，那么哪些环节可能会导致结论的差别?
定义:一般地，一组数据的第p百分位数是这样一个值，它使得这组数据中至少有p%的数据小于或等于这个值，且至少有(100-p)%的数据大于或等于这个值.
可以通过下面的步骤计算一组n个数据的第p百分位数:第1步，按从小到大排列原始数据.第2步，计算i=n×p%.第3步，若i不是整数，而大于i的比邻整数为j,则第p百分位数为第j项数据；若i是整数，则第p百分位数为第项与第(i+1)项数据的平均数.
第p百分位数的定义
判断正误1.若一组样本数据的10%分位数是23，则在这组数据中有10%的数据大于23.( )2.若一组样本数据的24%分位数是24，则在这组数据中至少有76%的数据大于或等于24.( )
不是．是指能够考取本科院校的同学占同学总数的百分比．
有70%的同学数学测试成绩在小于或等于85分．
班级人数为50的班主任老师说“90%的同学能够考取本科院校”， 这里的“90%”是百分位数吗？
(2)“这次数学测试成绩的第70百分位数是85分”这句话是什么意思？
思考1：第p百分位数有什么特点？
总体数据中的任意一个数小于或等于它的可能性是p.
中位数，相当于是第50百分位数.常用的分位数还有第25百分位数，第75百分位数.这三个分位数把一组由小到大排列后的数据分成四等份，因此称为四分位数.其中第25百分位数也称为第一四分位数或下四分位数等，第75百分位数也称为第三四分位数或上四分位数等，第1百分位数第5百分位数，第95百分位数和第99百分位数在统计中也经常被使用.
163.0 164.0 161.0 157.0 162.0 165.0 158.0 155.0 164.0 162.5 154.0 154.0 164.0 149.0 159.0 161.0 170.0 171.0 155.0 148.0 172.0 162.5 158.0 155.5 157.0 163.0 172.0
例2.根据下面女生的身高的样本数据，估计树人中学高一年级女生的第25,50,75百分位数.
解：把27名女生的样本数据按从小到大排序，可得148.0 149.0 154.0 154.0 155.0 155.0 155.5 157.0 157.0 158.0 158.0 159.0 161.0 161.0 162.0 162.5 162.5 163.0 163.0 164.0 164.0 164.0 165.0 170.0 171.0 172.0 172.0由25%×27=6.75, 50%×27=13.5, 75%×27=20.25,可知样本数据的第25,50,75百分位数为第7, 14,21项数据，分别为155.5,161,164.据此可以估计树人中学高一年级女生的第25,50,75百分位数分别约为155.5,161和164.
例3.根据下表或下图,估计月均用水量的样本数据的80%和95%分位数.
分析：统计表或统计图，与原始数据相比，它们损失了一些信息，例如由上表中可以知道在[16.2,19.2)内有5个数据，但不知道这5个数据具体是多少.此时，我们通常把它们看成均匀地分布在此区间上.
计算方法和计算中位数是一样的
下表为12名毕业生的起始月薪
根据表中所给的数据计算第85百分位数.
解:计算i＝12×85%＝10.2，所以所给数据的第85百分位数是从小到大的第11个数据3 130
1.下列一组数据的第25百分位数是(　　)2.1，3.0，3.2，3.8，3.4，4.0，4.2，4.4，5.3， B.3.0 C.4.4 D.2.5
解　把该组数据按照由小到大排列，可得：2.1，3.0，3.2，3.4，3.8，4.0，4.2，4.4，5.3，5.6，由i＝10×25%＝2.5，不是整数，则第3个数据3.2，是第25百分位数.
2.知100个数据的第75百分位数是9.3，则下列说法正确的是(　　)A.这100个数据中一定有75个数小于或等于9.3B.把这100个数据从小到大排列后，9.3是第75个数据C.这100个数从小到大排列后，9.3是第75个数和第76个数的平均数D.这100个数从小到大排列后，9.3是第75个数和第74个数的平均数
解析：因为100×75%＝75为整数，所以第75个数据和第76个数据的平均数为第75百分位数，是9.3，选C.
3.某公司2018年在各个项目中总投资500万元,如图是几类项目的投资占比情况,已知在1万元以上的项目投资中,少于3万元的项目投资占 ,那么不少于3万元的项目投资共有(　　)A.56万元B.65万元C.91万元D.147万元
4. 为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,你能估计一下60株树木的第50百分位数和第75百分位数吗?
解:由题意知分别落在各区间上的频数为在[80,90)上有60×0.15=9,在[90,100)上有60×0.25=15,在[100,110)上有60×0.3=18,在[110,120)上有60×0.2=12,在[120,130]上有60×0.1=6.从以上数据可知第50百分位数一定落在区间[100,110)上,
综上可知,第50百分位数和第75百分位数分别估计为103.3 cm,112.5 cm.
5.从某珍珠公司生产的产品中，任意抽取12颗珍珠，得到它们的质量(单位：g)如下：
7.9，9.0，8.9，8.6，8.4，8.5，8.5，8.5，9.9，7.8，8.3，8.0.(1)分别求出这组数据的第25，50，95百分位数；
解　(1)将所有数据从小到大排列，得7.8，7.9，8.0，8.3，8.4，8.5，8.5，8.5，8.6，8.9，9.0，9.9，因为共有12个数据，所以12×25%＝3，12×50%＝6，12×95%＝11.4，
2)请你找出珍珠质量较小的前15%的珍珠质量；
(2)因为共有12个数据，所以12×15%＝1.8，则第15百分位数是第2个数据为7.9.即产品质量较小的前15%的产品有2个，它们的质量分别为7.8，7.9.
解　(1)将所有数据从小到大排列，得7.8，7.9，8.0，8.3，8.4，8.5，8.5，8.5，8.6，8.9，9.0，9.9，
7.9，9.0，8.9，8.6，8.4，8.5，8.5，8.5，9.9，7.8，8.3，8.0.
3)若用第25，50，95百分位数把公司生产的珍珠划分为次品、合格品、优等品和特优品，依照这个样本的数据，给出该公司珍珠等级的划分标准.
(3)由(1)可知样本数据的第25百分位数是8.15 g，第50百分位数为8.5 g，第95百分位数是9.9 g，所以质量小于或等于8.15 g的珍珠为次品，质量大于8.15 g且小于或等于8.5 g的珍珠为合格品，质量大于8.5 g且小于或等于9.9 g的珍珠为优等品，质量大于9.9 g的珍珠为特优品.
（2）由(1)可知，当y＝260时，x＝400，即用电量不超过400千瓦时的占80%，
用电量不超过400千瓦时的占80%，所以75%分位数为m在[300,400)内，所以0.6＋(m－300)×0.002＝0.75,解得m＝375千瓦时，即用电量的75%分位数为375千瓦时．
（3）设75%分位数为m，因为用电量低于30千瓦时的所占 比例为(0.001＋0.002＋0.003)×100＝60%，