




苏科版九年级上册2.2 圆的对称性教课内容课件ppt
展开圆是中心对称图形,对称中心是圆心。圆还具有旋转不变性:圆绕着它的圆心旋转任意角度,都能与原来的圆重合。
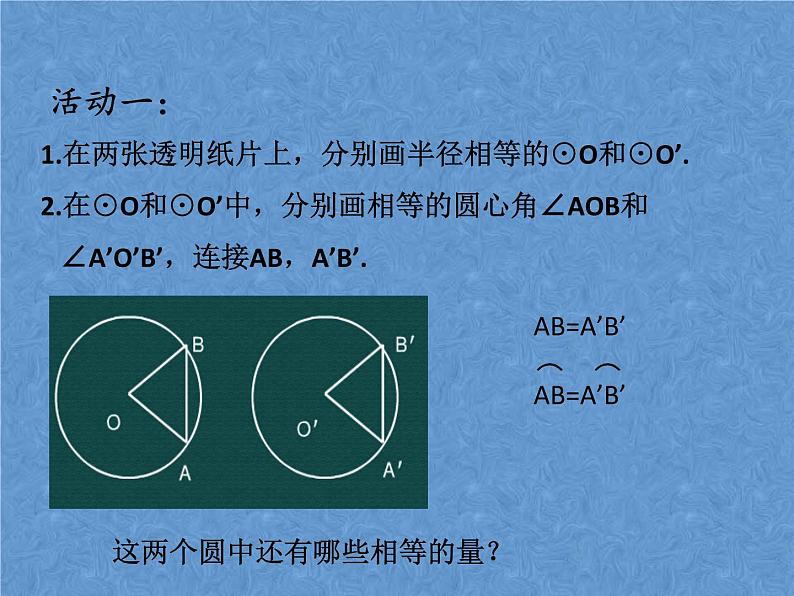
1.在两张透明纸片上,分别画半径相等的⊙O和⊙O’.2.在⊙O和⊙O’中,分别画相等的圆心角∠AOB和 ∠A’O’B’,连接AB,A’B’.
这两个圆中还有哪些相等的量?
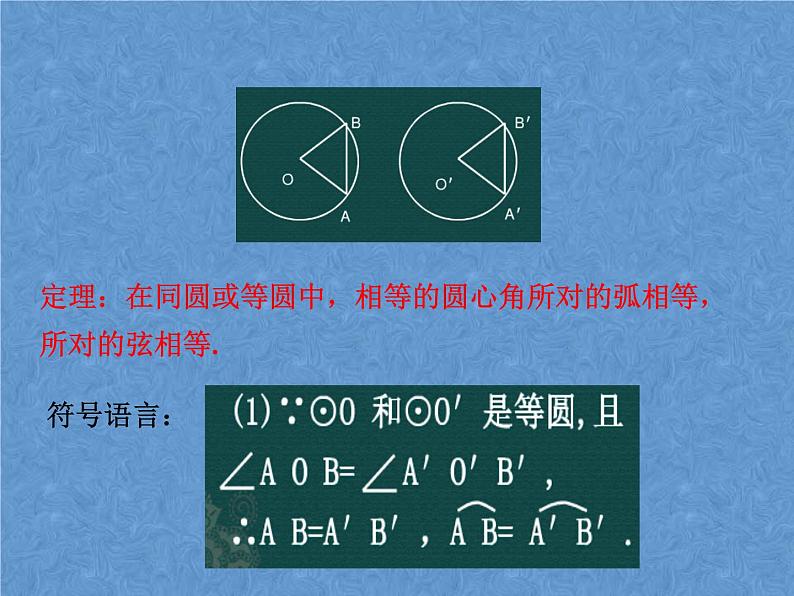
定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
在同圆或等圆中,如果两条弧相等,那么它们所对的弦相等,它们所对的圆心角相等.
思考:在同圆或等圆中,如果圆心角所对的弧相等,那么它们所对的弦相等吗?这两个圆心角相等吗?为什么?
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,它们所对的弧相等
思考:在同圆或等圆中,如果圆心角所对的弦相等,那么它们所对的弧相等吗?这两个圆心角相等吗?为什么?
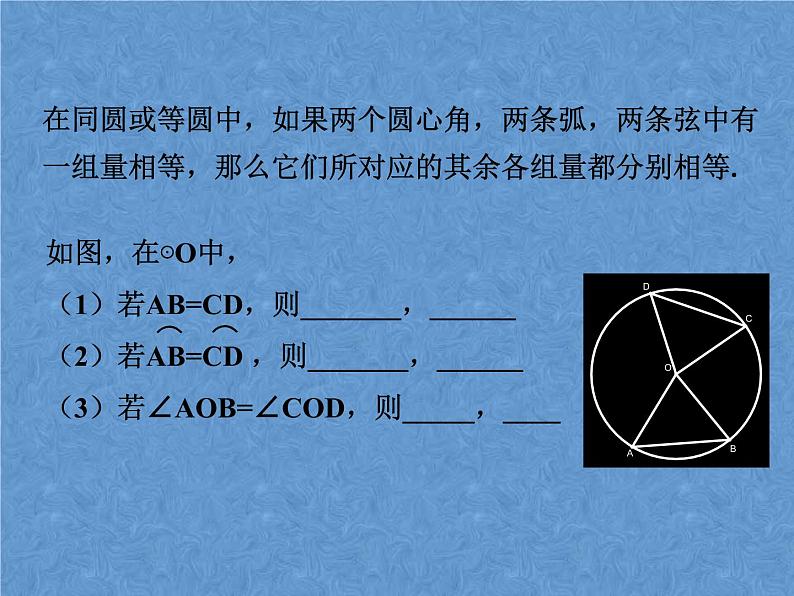
在同圆或等圆中,如果两个圆心角,两条弧,两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
例1: 如图,AB、AC、BC是⊙O的弦,∠AOC=∠BOC,∠ABC与∠BAC相等吗?为什么?
若∠ABC与∠BAC, 则∠AOC=∠BOC吗?
弧的度数与它所对的圆心角的度数相等.
如图,在△ABC中,∠C=90°,∠B=28°,以点C为圆心,CA为半径的圆交AB于点D、BC于点E.求弧AD、DE的度数数.
1.圆是中心对称图形,圆心是它的对称中心。
2.在同圆或等圆中,如果两个圆心角,两条弧,两条弦中有一组量相等,那么它们所对应的其余各组都分别相等。
3.弧的度数与它所对的圆心角的度数相等.
2.2 圆的对称性(2)
在直径为650mm的圆柱形油罐内装进一些油后,其横截面如图.若油面宽AB=600mm,求油的最大深度.
结论:圆是轴对称图形,过圆心的任意一条直线都是它的对称轴.
结论:(1)AE=BE;
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
∵ CD是直径,
下列图形是否具备垂径定理的条件?
垂径定理的几个基本图形:
2.如图,OE⊥AB于点E,若⊙O的半径为10cm,OE=6cm,则AB= cm.
解:连接OA.∵ OE⊥AB,
∴ AB=2AE=16cm.
3.如图,⊙O直径为10,弦AB的长为8,点P在AB上运动.则OP的取值范围是___________________.
4.如图,CD是⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,求直径CD的长.
∵ CD是直径,OE⊥AB,
设OA=x,则OE=x-1,由勾股定理得
x2=52+(x-1)2 .
∴ CD=2OA=26.
即直径CD的长为26.
5.如图,过⊙O内一点P画弦AB,使P是AB的中点.
例2 如图,在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D.AC与BD相等 吗?为什么?
如图,AB、CD是⊙O的两条弦,AB∥CD. 和 相等吗?为什么?
数学苏科版2.2 圆的对称性集体备课ppt课件: 这是一份数学苏科版<a href="/sx/tb_c17325_t3/?tag_id=26" target="_blank">2.2 圆的对称性集体备课ppt课件</a>,共27页。PPT课件主要包含了想一想,做一做,③AP=BP,AB是⊙O的一条弦,由①CD是直径,②CD⊥AB,证一证,连接OAOB,则OA=OB,∴AP=BP等内容,欢迎下载使用。
苏科版九年级上册2.2 圆的对称性评优课ppt课件: 这是一份苏科版九年级上册2.2 圆的对称性评优课ppt课件,共32页。PPT课件主要包含了折痕过圆心,折叠法,圆有无数条对称轴,你能证明你的猜想吗,CPDP,在△OCD中,∴PCPD,∠BOC∠BOD,垂直于弦,平分弦等内容,欢迎下载使用。
数学九年级上册2.2 圆的对称性优质课教学课件ppt: 这是一份数学九年级上册2.2 圆的对称性优质课教学课件ppt,共15页。PPT课件主要包含了情境引入,对称轴,新课讲解,操作与思考,你能证明上述结论吗,叠合法,垂径定理,几何语言,例题精讲,课堂练习等内容,欢迎下载使用。













