数学八年级上册第十二章 全等三角形12.2 三角形全等的判定评课课件ppt

这是一份数学八年级上册第十二章 全等三角形12.2 三角形全等的判定评课课件ppt，共23页。PPT课件主要包含了知识回顾，学习目标，课堂导入，新知探究，跟踪训练，ABED，∠ACB∠ECD，随堂练习，三角形全等的判定，分类探讨等内容，欢迎下载使用。

1.什么叫全等三角形？
能够完全重合的两个三角形叫做全等三角形.
2.三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”).
符号语言表示：在△ABC和△A'B'C'中， AB=A'B'， AC=A'C'， BC=B'C'， ∴△ABC≌△A'B'C' (SSS).
3.两边和它们的夹角分别相等的两个三角形全等（可以简写成“边角边”或“SAS”）.
符号语言表示：在△ABC和△A′B′C′中， AB=A′B′， ∠B=∠B′， BC=B′C′， ∴△ABC≌△A′B′C′(SAS).
1.理解并掌握三角形全等判定“角边角”条件的内容.2.熟练利用“角边角”条件证明两个三角形全等.3.通过探究判定三角形全等条件的过程，提高分析和解决问题的能力.
先任意画出一个△ABC，再画一个△A′B′C′，使得AB=A′B′，∠A=∠A′，∠B=∠B′（即两角和它们的夹边分别相等）.此时的△ABC和△A′B′C′全等吗？
作法: (1)画A′B′=AB. (2)在A′B′的同旁画∠DA′B′=∠A，∠EB′A′=∠B， A′D，B′E相交于点C′. (3)△A′B′C′即为所作三角形.
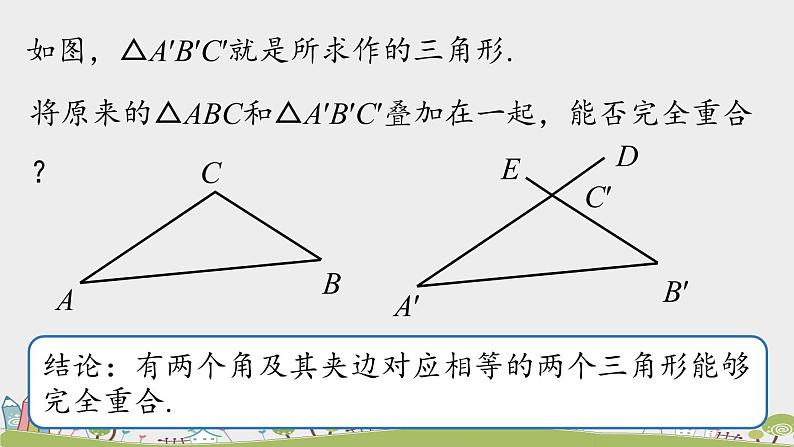
如图，△A′B′C′就是所求作的三角形.
将原来的△ABC和△A′B′C′叠加在一起，能否完全重合？
结论：有两个角及其夹边对应相等的两个三角形能够完全重合.
判定3：两角和它们的夹边分别相等的两个三角形全等（可以简写成“角边角”或“ASA”）.
符号语言表示：在△ABC和△A′B′C′中， ∠B=∠B′， BC=B′C′， ∠C=∠C′， ∴△ABC≌△A′B′C′(ASA).
知识点 三角形全等的基本事实：角边角(ASA)
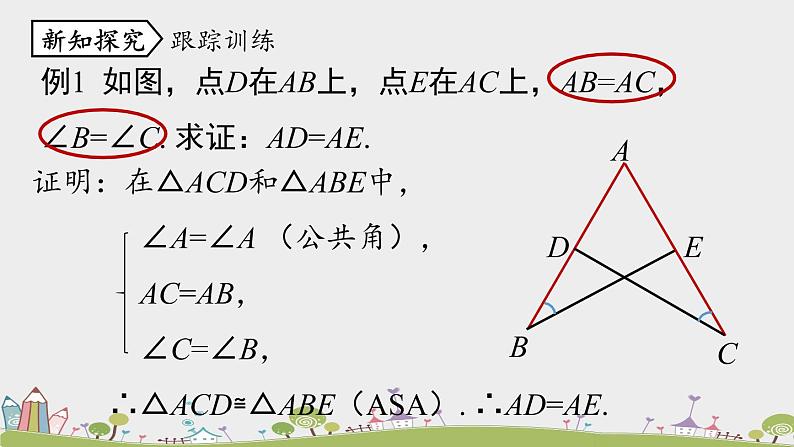
例1 如图，点D在AB上，点E在AC上，AB=AC，∠B=∠C. 求证：AD=AE.
证明：在△ACD和△ABE中， ∠A=∠A （公共角）， AC=AB， ∠C=∠B， ∴△ACD≌△ABE（ASA）. ∴AD=AE.
例2 如图，在△ABC和△DEF中，∠A=∠D，∠B=∠E，BC=EF.求证：△ABC≌△DEF.
证明：在△ABC和△DEF中， ∠A=∠D， BC=EF， ∠B=∠E， ∴△ABC≌△DEF（ASA）.
分析：BC，EF不是已知两对角的夹边，在三角形中，知道两个角的关系，利用三角形内角和定理可以求得第三个角之间的关系.通过转化来构造“ASA”的判定条件.
证明：∵在△ABC和△DEF中，∠A=∠D,∠B=∠E, ∴∠C=∠F. 在△ABC和△DEF中， ∴△ABC≌△DEF（ASA）.
∠B=∠E， BC=EF， ∠C=∠F，
例3 如图，AB⊥BC，AD⊥DC，垂足分别为点B，点D，∠1=∠2.求证：AB=AD.
证明：∵AB⊥BC，AD⊥DC， ∴∠ABC=∠ADC=90°. ∵在△ABC和△ADC中， ∠1 =∠2，∠ABC=∠ADC， ∴∠ACB=∠ACD.
在△ABC和△ADC中， ∠1=∠2， AC=AC（公共边）， ∠ACB=∠ACD， ∴△ABC≌△ADC（ASA）， ∴AB=AD.
例4 如图，要测量池塘两岸相对的两点A,B的距离，可以在池塘外取AB的垂线BF上的两点C,D,使BC=CD.再画出BF的垂线DE，使得E与A，C在一条直线上，这时测得DE的长就是AB的长，为什么？
解：由题可知AB⊥BC，ED⊥DC， 则∠ABC=∠EDC=90°. 在△ABC和△EDC中，
∠ABC=∠EDC， BC=DC， ∠ACB=∠ECD， ∴△ABC≌△EDC（ASA）. ∴AB=ED，即DE的长就是AB的长.
1.如下图，已知∠B=∠D，DC=BC，还需要给出什么条件，即可得出△ABC≌△EDC.根据是什么？
条件（ ），根据（ ）.条件（ ），根据（ ）.
两边及其夹角分别相等的两个三角形全等
两角及其夹边分别相等的两个三角形全等
2.如图，已知∠1=∠2，∠C=∠D.求证：AC=AD.
证明：∵∠1=∠2，∠C=∠D， ∴∠ABC=∠ABD . 在△ABC和△ABD中， ∠1=∠2， AB=AB（公共边）， ∠ABC=∠ABD， ∴△ABC≌△ABD（ASA）. ∴AC=AD.
3.如图，已知D是AC上一点，AB=DA，DE//AB，∠B=∠DAE.求证：△ABC≌△DAE.
证明：∵DE//AB，∴ ∠CAB=∠EDA. 在△ABC和△DAE中， ∠CAB=∠EDA， AB=DA， ∠B=∠DAE， ∴△ABC≌△DAE（ASA）.
有平行线就可以转化出相等的角.
4.如图，在Rt△ABC中，∠ACB=90°，BC=2cm，CD⊥AB，在AC上取一点E，使EC=BC，过点E作EF⊥AC交CD的延长线于点F，若EF=5cm，求AE的长.
解：∵CD⊥AB， ∴∠A+∠ACD=90°.∵∠ACB=90°， ∴∠A+∠B=90°. ∴∠B=∠ACD.∵EF⊥AC，∴∠FEC=90°. ∴∠ACB=∠FEC.
∠B=∠FCE， 在△ACB和△FEC中， BC=CE， ∠ACB=∠FEC，∴△ACB≌△FEC（ASA）. ∴ AC=EF.∵BC=2cm，EF=5cm, ∴ AE=3cm.
1.如图，已知∠1=∠2，∠E=∠C，AC=AE.求证：AB=AD，∠B=∠D.
证明：∵∠1=∠2， ∴∠1+∠EAC=∠2+∠EAC， 即∠BAC=∠DAE. 在△ABC和△ADE中，