初中数学人教版七年级下册5.2.1 平行线第2课时导学案及答案

这是一份初中数学人教版七年级下册5.2.1 平行线第2课时导学案及答案，共4页。学案主要包含了学习目标，学习重点，学习难点，学具准备，自主学习，合作探究，反馈提高，达标测评等内容，欢迎下载使用。

1、使学生掌握平行线的四种判定方法，并初步运用它们进行简单的推理论证。
2、初步学会简单的论证和推理，认识几何证明的必要性和证明过程的严密性。
【学习重点】在观察实验的基础上进行公理的概括与定理的推导
【学习难点】定理形成过程中的逻辑推理及其书面表达。
【学具准备】三角板
【自主学习】
1、预习疑难： 。
2、填空：经过直线外一点,_____ ___与这条直线平行.
【合作探究】（一）平行线判定方法1：
1、观察思考：过点P画直线CD∥AB的过程，三角尺起了什么作用？
图中，∠1和∠2什么关系？
2、判定方法1： 应用格式：
。∵∠1＝∠2（已知）
简单说成： 。 ∴AB∥CD（同位角相等，两直线平行）
应用：木工师傅使用角尺画平行线，有什么道理？
（二）平行线判定方法2、3：
思考：教材14页（试着写出推理过程）
判定方法2： 应用格式：
。∵∠2＝∠3（已知）
简单说成： 。 ∴a∥b（内错角相等，两直线平行）
2、将上题中条件改变为∠2＋∠4＝180°，能得到a∥b吗？（试写出推理过程）
判定方法3： 应用格式：
。 ∵∠2＋∠4＝180°（已知）
简单说成： 。∴a∥b（同旁内角互补，两直线平行）
（三）数学思想：教材15页探究。
【反馈提高】
（一）例 教材15页
（二）练一练：教材15页练习1、2、3
（三）总结直线平行的条件

（1） （2）
方法1：若a∥b，b∥c，则a∥c。即两条直线都与第三条直线平行，这两条直线也互相平行。
方法2：如图1，若∠1＝∠3，则a∥c。即 。
方法3：如图1，若 。
方法4：如图1，若 。
方法5：如图2，若a⊥b，a⊥c,则b∥c。即在同一平面内，垂直于同一条直线的两条直线互相平行。
【达标测评】
（一）选择题:
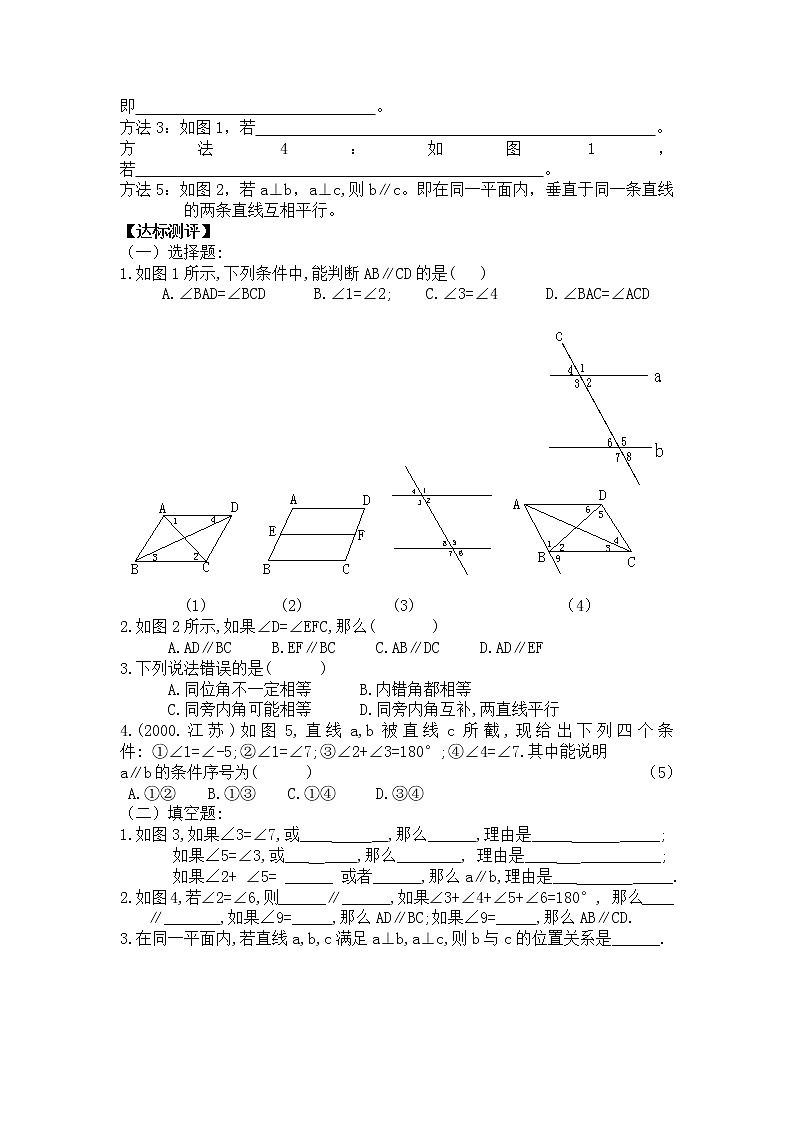
1.如图1所示,下列条件中,能判断AB∥CD的是( )毛
A.∠BAD=∠BCD B.∠1=∠2; C.∠3=∠4 D.∠BAC=∠ACD
(1) (2) (3) （4）
2.如图2所示,如果∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF
3.下列说法错误的是( )
A.同位角不一定相等 B.内错角都相等
C.同旁内角可能相等 D.同旁内角互补,两直线平行
4.(2000.江苏)如图5,直线a,b被直线c所截,现给出下列四个条件:①∠1=∠-5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明
a∥b的条件序号为( ) （5）
A.①② B.①③ C.①④ D.③④
（二）填空题:
1.如图3,如果∠3=∠7,或____ __,那么______,理由是_____ _____;
如果∠5=∠3,或___ ____,那么________, 理由是____ __________;
如果∠2+ ∠5= ______ 或者______,那么a∥b,理由是___ _____.
2.如图4,若∠2=∠6,则______∥______,如果∠3+∠4+∠5+∠6=180°, 那么____∥_______,如果∠9=_____,那么AD∥BC;如果∠9=_____,那么AB∥CD.
3.在同一平面内,若直线a,b,c满足a⊥b,a⊥c,则b与c的位置关系是______.
4.如图所示,BE是AB的延长线,量得∠CBE=∠A=∠C.
(1)由∠CBE=∠A可以判断______∥______,根据是_________.
(2)由∠CBE=∠C可以判断______∥______,根据是_________.
六、【拓展延伸】
1、已知直线a、b被直线c所截,且∠1+∠2=180°,
试判断直线a、b的位置关系,并说明理由.
2、如图，已知，，试问EF是否平行GH，并说明理由。
3.如图所示,已知∠1=∠2,AC平分∠DAB,试说明DC∥AB.
如图所示,已知直线EF和AB,CD分别相交于K,H,且EG⊥AB,∠CHF=600,∠E=-30°,试说明AB∥CD.
5、提高训练:
如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为-什么?