数学九年级上册23.2.3 关于原点对称的点的坐标优秀课件ppt

这是一份数学九年级上册23.2.3 关于原点对称的点的坐标优秀课件ppt，共19页。PPT课件主要包含了第一象限，第三象限，第二象限，第四象限，y轴上，x轴上，G00，坐标原点，P-23，B23等内容，欢迎下载使用。

1.下列各点分别在坐标平面的什么位置上？
A（5，8）B（0 ， 5）C（－2，－3）D（－10，0）E（－2.8，6.2）F（7，－2）
A（-2,- 3 ）
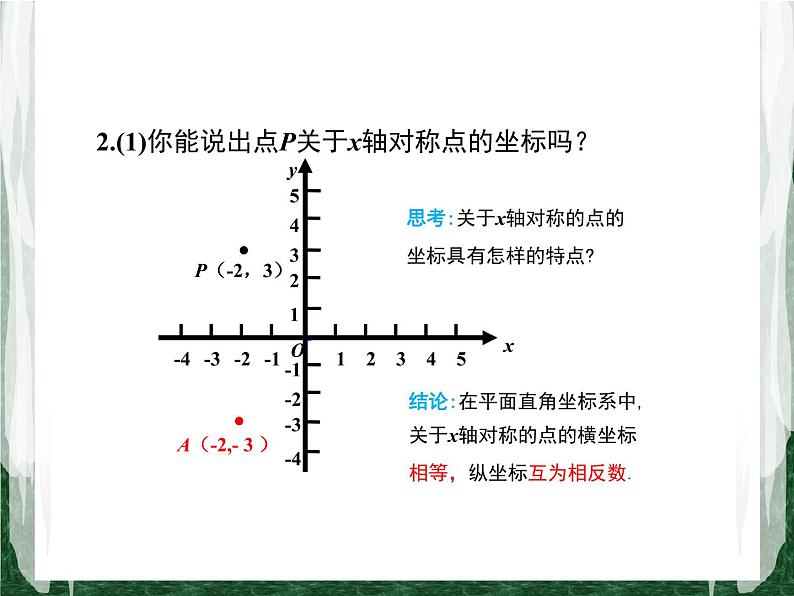
2.(1)你能说出点P关于x轴对称点的坐标吗？
思考:关于x轴对称的点的坐标具有怎样的特点?
结论:在平面直角坐标系中,关于x轴对称的点的横坐标相等，纵坐标互为相反数.
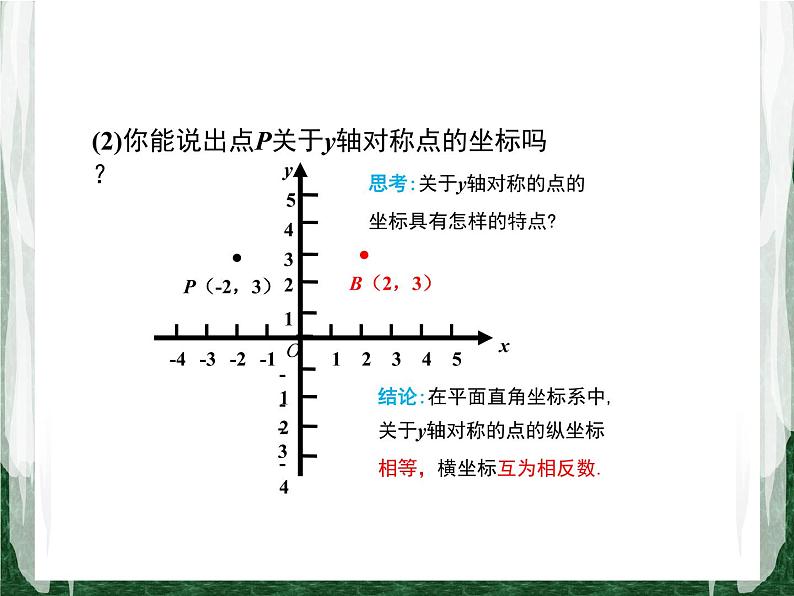
(2)你能说出点P关于y轴对称点的坐标吗？
思考:关于y轴对称的点的坐标具有怎样的特点?
结论:在平面直角坐标系中,关于y轴对称的点的纵坐标相等，横坐标互为相反数.
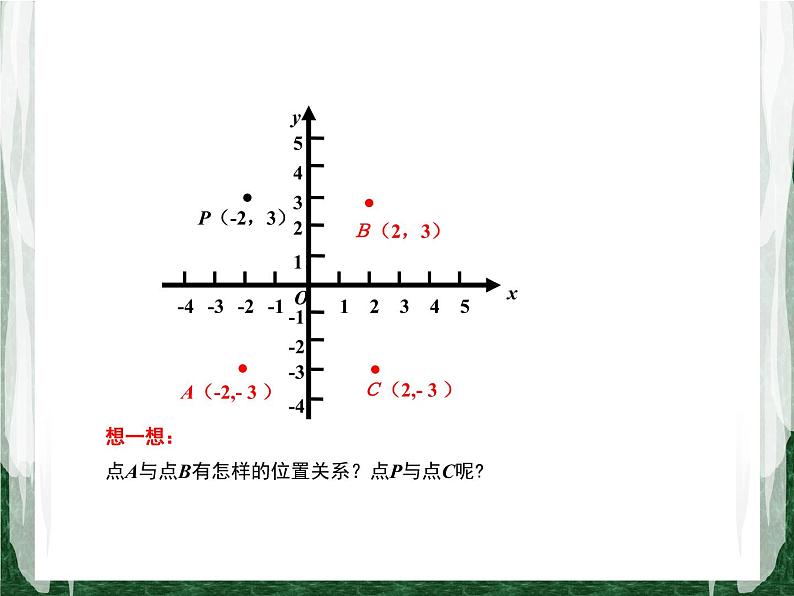
想一想：点A与点B有怎样的位置关系？点P与点C呢?
1.关于原点对称的点的坐标特点
提示： 　　第一象限内的点关于原点的对称点在第三象限，第二象限内的点关于原点的对称点在第四象限，坐标轴上的点关于原点的对称点仍在坐标轴上.
两个点关于原点对称时，它们的坐标符号相反，即点P(x，y)关于原点的对称点为P(-x，-y).
2.关于坐标轴对称与关于原点对称的区别
3.平面直角坐标系内中心对称作图的方法
方法2：先求对称点的坐标，再描点画图.
方法1：用中心对称的方法，延长再截取；
例1：在直角坐标系中，作出下列已知点关于原点O的对称点，并写出它们的坐标.这些坐标与已知点的坐标有什么关系？A (4，0)， B (0，-3)， C (2，1)， D (-1，2)，E (-3，-4)
解：A，B，C，D，E点关于原点O的对称点,如图所示.
各点及其对称点的坐标如下：
归纳 两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点为P'(-x,-y).
例2：利用关于原点对称的点的坐标的关系，作出与△ABC关于原点对称的图形.
解:A(-4,1)关于原点的对称点为A'(4,-1)，B(-1,-1)关于原点的对称点为B'(1,1),C(-3,2)关于原点的对称点为C'(3,-2).依次连接就可得到与△ABC关于原点对称的△A'B'C'.
1.若点P(a,1)与点Q(5, b)关于原点对称,则a+b=_______.
2.点M(5,6)和点N是关于原点对称的两点,则点N在第________象限.
3.写出下列各点关于原点的对称点A'，B'，C'，D' 的坐标：A(3，1),B(-2，3),C(-1，-2),D(2，-3).
4.在如图所示编号为①、②、③、④的四个三角形中，关于y轴对称的两个三角形的编号为 　；关于坐标原点O对称的两个三角形的编号为________.
5、如图，已知A的坐标为( ,2),点B的坐标为（-1， )，菱形ABCD的对角线交于坐标原点O.求C，D两点的坐标.
解:因为点A和C关于原点对称所以点C的坐标是( , -2 ).因为点D和B关于原点对称,所以点Ｄ的坐标是(1,　　).
6、△ABC的顶点坐标分别为A(5,0),B (-1,0), C(-2,3). 作出与△ABC关于原点O对称的图形△A'B'C'.
关于原点对称的点的坐标
P (x，y)关于原点的对称点为P′(-x，-y)
方法1：用中心对称的方法，延长再截取方法2：先求对称点的坐标，再描点画图