人教版九年级上册21.1 一元二次方程一等奖课件ppt

这是一份人教版九年级上册21.1 一元二次方程一等奖课件ppt，共22页。PPT课件主要包含了知识梳理，基本概念，一元二次方程，一般形式，一元二次方程的解，是整式方程，只含有一个未知数，未知数的最高次数是2，直接开平方法，配方法等内容，欢迎下载使用。

ax2+bx+c=0(a≠0)
使一元二次方程左右两边相等的未知数的值
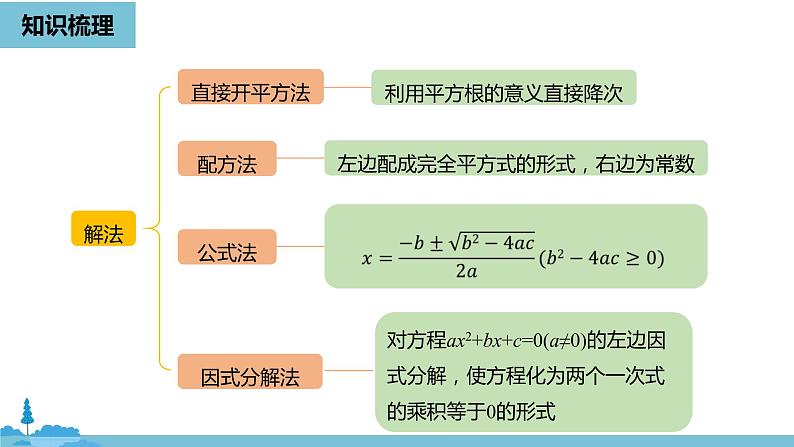
利用平方根的意义直接降次
对方程ax2+bx+c=0(a≠0)的左边因式分解，使方程化为两个一次式的乘积等于0的形式
左边配成完全平方式的形式，右边为常数
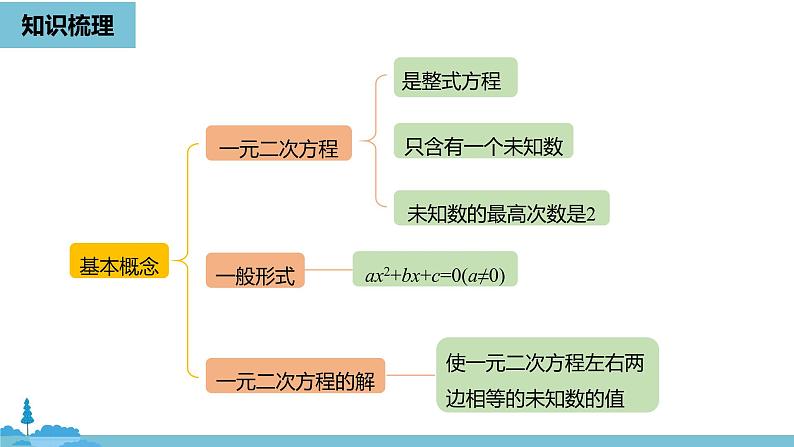
一元二次方程的基本概念
1.定义： 只含有一个未知数的整式方程，并且都可以化为 ax2＋bx＋c＝0(a，b，c为常数，a≠0)的形式，这样的方程叫做一元二次方程．2.一般形式：
ax2 ＋ bx ＋c＝0 (a，b，c为常数，a≠0)
3.项数和系数： ax2 ＋ bx ＋c＝0 (a，b，c为常数，a≠0)二次项： ax2 二次项系数：a一次项： bx 一次项系数：b常数项：c4.注意事项： (1)只含有一个未知数； (2)未知数的最高次数为2； (3)二次项系数不为0； (4)整式方程．
x2 + px + q = 0 （p2 - 4q ≥0）
(x+m)2＝n（n ≥ 0）
ax2 + bx +c = 0(a≠0 ， b2 - 4ac≥0)
(x + m) （x + n）＝0
各种一元二次方程的解法及适用类型
若关于x的方程(m-1)x2+mx-1=0是一元二次方程，则m的取值范围是( )A. m≠1 B. m=1 C. m≥1 D. m≠0
解：本题考查了一元二次方程的定义，即方程中必须保证有二次项(二次项系数不为0)，因此它的系数m-1≠0，即m≠1，故选A.
解：根据一元二次方程根的定义可知，将x=0代入原方程一定会使方程左右两边相等，故只要把x=0代入就可以得到以m为未知数的方程，即m2-1=0，解得m=±1.又二次项系数不能为0，所以m≠1，即m=-1.
若关于x的一元二次方程(m-1)x2+x+m2-1=0有一个根为0，则m= .
这种解题方法我们称之为“有根必代”.
解：配方法的关键是配上一次项系数一半的平方.
用配方法解方程x2-2x-5=0时，原方程应变为( ) A. (x-1)2=6 B.(x+2)2=9 C. (x+1)2=6 D.(x-2)2=9
解：解方程x2-13x+36=0得 x1=9，x2=4，即第三边长为9或4．边长为9，3，6不能构成三角形；而4，3，6能构成三角形，所以三角形的周长为3+4+6=13，故选A．
三角形两边长分别为3和6，第三边的长是方程x2﹣13x+36=0的根，则该三角形的周长为( )A.13 B.15 C.18 D.13或18
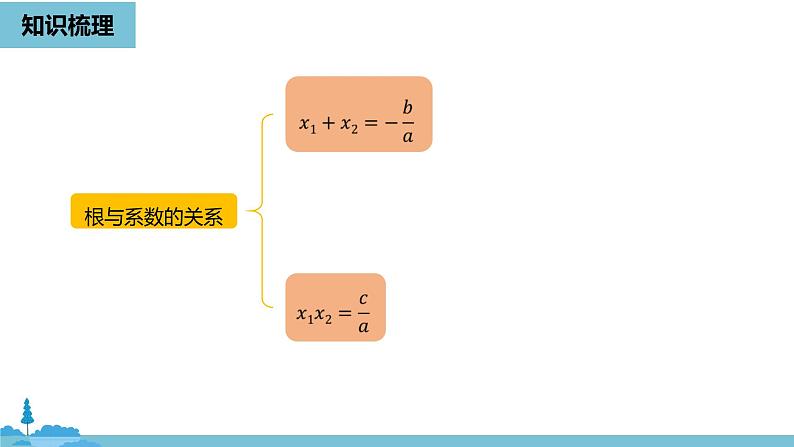
已知一元二次方程x2－4x－3＝0的两根分别为m，n，则m2－mn＋n2＝ ．
解：根据根与系数的关系可知 m+n=4，mn=-3. m2－mn＋n2=m2+n2-mn=(m+n)2-3mn=42-3 ×(-3)=25.
(1) 方程5x2-x-3=x2-3+x的二次项系数是 ，一次项系数是 ，常数项是 .
(2) 一元二次方程x2+px-2=0的一个根为2，则 p 的值为 .
解：把 x=2代入方程 x2+px-2=0得 4+2p-2=0，解得 p=-1．
菱形ABCD的一条对角线长为6，边AB的长是方程x2-7x+12=0的一个根，则菱形ABCD的周长为( ) A. 16 B. 12 C. 16或12 D. 24
解：方程x2-7x+12=0可转化为(x-3)(x-4)=0，x-3=0或 x-4=0，所以x1=3，x2=4，因为菱形ABCD的一条对角线长为6，所以边AB的长是4，所以菱形ABCD的周长为16．故选A．
用公式法和配方法分别解方程：x2-4x-1=0(要求写出必要解题步骤).
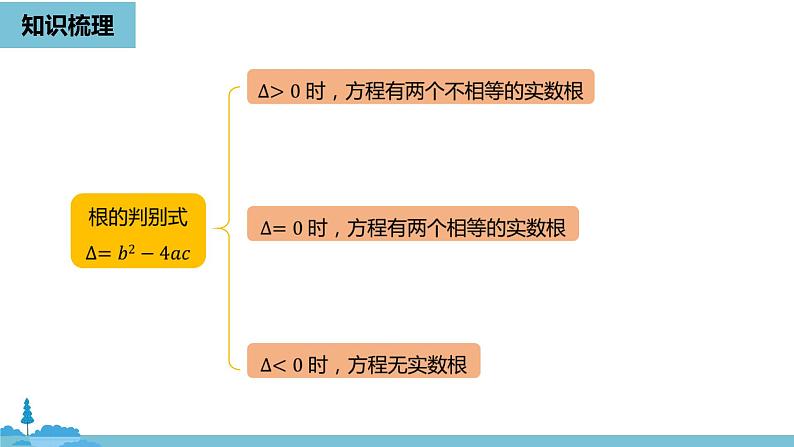
下列所给方程中，没有实数根的是( )A. x2+x=0 B. 5x2-4x-1=0 C.3x2-4x+1=0 D. 4x2-5x+2=0
若关于 x 的一元二次方程 x2-x+m=0 有两个不相等的实数根，则 m 的值可能是　　(写出一个即可)．