





- 5.2 视图 5.2.1由几何体到三视图 课件PPT 课件 9 次下载
- 5.2 视图 5.2.2由三视图到几何体 课件PPT 课件 8 次下载
- 6.1反比例函数 课件PPT 课件 15 次下载
- 6.2反比例函数的图像与性质 6.2.1反比例函数的图像 课件PPT 课件 18 次下载
- 6.3反比例函数的应用 课件PPT 课件 12 次下载
初中数学2 反比例函数的图象与性质优质课ppt课件
展开1.能根据反比例函数的图像和表达式探索、理解反比例函数的性质,并能根据图象求相应的函数表达式.2.能运用反比例函数的图像和性质解决相关问题.(重点)
(1)如何画反比例函数的图象呢?(2)其步骤是怎样的呢?
知识点1 反比例函数的性质
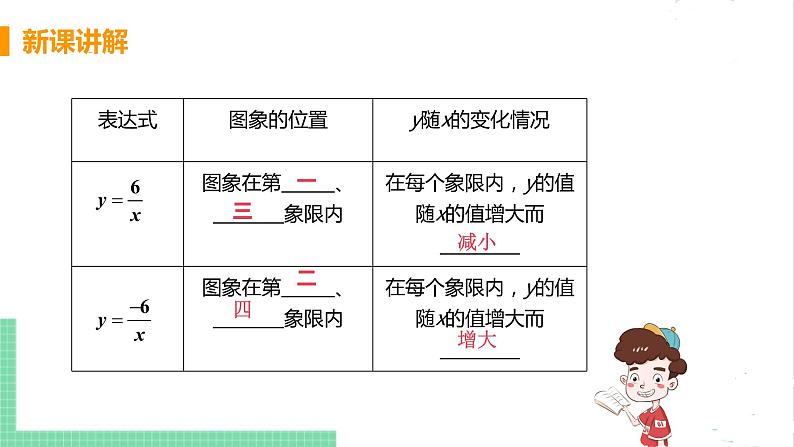
根据反比例函数 与 的表达式及图像,探究下列问题:
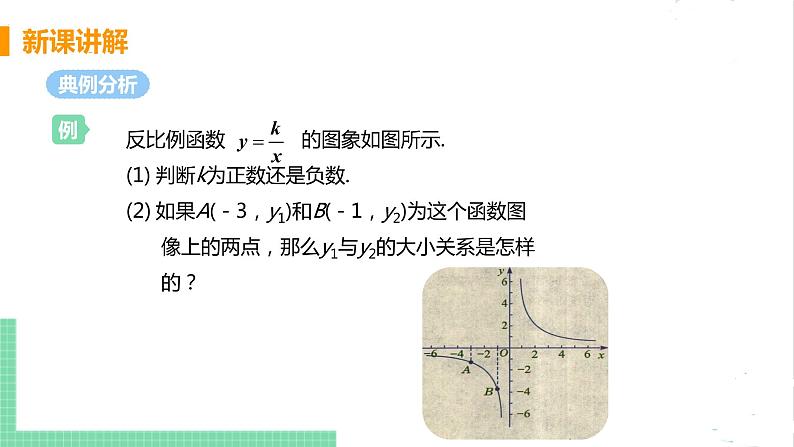
反比例函数 的图象如图所示.(1)判断k为正数还是负数.如果A(-3,y1)和B(-1,y2)为这个函数图 像上的两点,那么y1与y2的大小关系是怎样 的?
解:(1)因为反比例函数 的图象在第一、三象限, 所以k>0.由k>0可知,在每个象限内,y的值随x的值增 大而减小, ∵-3<-1, ∴y1>y2.
根据反比例函数的增减性比较函数值大小的方法: 利用反比例函数的增减性来比较函数值的大小时,如果给定的两点或几点能够确定在同一象限的分支上时,可以直接利用反比例函数的性质解答;如果给定的两点或几点不能够确定在同一象限的分支上时,则不能利用反比例函数的性质比较,需要根据函数的图象和点的位置用数形结合思想来比较或利用特殊值法通过求值来进行比较.
已知反比例函数 ,当1<x<3 时,y的最小整数值是( ) A.3 B.4 C.5 D.6
在反比例函数 的每一条曲线上,y都随着x的增大而减小,则k的值可以是( ) A.-1 B.1 C.2 D.3
知识点2 反比例函数中K的几何性质
双曲线的几何特性: 过双曲线 上的任意一点向两坐标轴作垂线,与两坐标轴围成的矩形面积等于|k|,连接该点与原点,还可得出两个直角三角形,这两个直角三角形的面积都等于 .
如图,两个反比例函数 和 在第一象限内的图象分别是C1和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为________.导引:根据反比例函数中k的几何意义,得△POA和△BOA的面积分别为2和1,于是阴影部分的面积为1.
求阴影部分面积的方法: 当它无法直接求出时,一般都采用“转化”的方法,将它转化为易求图形面积的和或差来进行计算.如本例就是将阴影部分面积转化为两个与比例系数相关的特殊三角形的面积的差来求,要注意转化思想和作差法的运用.
如图,点A为反比例函数 图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为( ) A.-4 B.4 C.-2 D.2
当K小于0,在每一象限内,y的值随x值的增大而增大
当K大于0,在每一象限内,y的值随x值的增大而减小
关于直线y=+x或y=-x对称
1.已知反比例函数y=-6x,下列结论不正确的是( )A.图像必经过点(-3,2)B.图像位于第二、四象限C.若x<-2,则0<y<3D.在每一象限内,y随x值的增大而减小2.在反比例函数y=m-7x的图像的每一支上,y随x值的增大而减小,则m的取值范围是( )A.m>7 B.m<7 C.m=7 D.m≠7
3.作出函数y=12x的图像,并根据图像解答下列问题:(1)当x=-2时,求y的值;(2)当2<y<3时,求x的取值范围;(3)当-4<x<-2时,求y的取值范围.
解:图像如答图.(1)当x=-2时,y=12-2=-6.(2)当y=2时,x=122=6;当y=3时,x=123=4,则x的取值范围是4<x<6.(3)当x=-4时,y=12-4=-3;当x=-2时,y=-6,则y的取值范围是-6<y<-3.
初中湘教版1.2 反比例函数的图像与性质获奖课件ppt: 这是一份初中湘教版1.2 反比例函数的图像与性质获奖课件ppt,共25页。PPT课件主要包含了学习目标,k20b0,k10,k<0,k>0,想一想,练一练,<x<5等内容,欢迎下载使用。
湘教版九年级上册1.2 反比例函数的图像与性质评优课课件ppt: 这是一份湘教版九年级上册1.2 反比例函数的图像与性质评优课课件ppt,共24页。PPT课件主要包含了学习目标,解列表如下,典例精析,总结归纳,练一练,m>2,解如图所示,能力提升,三象限,四象限等内容,欢迎下载使用。
初中数学湘教版九年级上册第1章 反比例函数1.2 反比例函数的图像与性质评优课ppt课件: 这是一份初中数学湘教版九年级上册第1章 反比例函数1.2 反比例函数的图像与性质评优课ppt课件,共26页。PPT课件主要包含了学习目标,我们可以证明,方法归纳,列表如下,练一练,1列表,2列表,所以有,解得m2等内容,欢迎下载使用。













