人教版八年级下册17.1 勾股定理优秀ppt课件

这是一份人教版八年级下册17.1 勾股定理优秀ppt课件，共31页。PPT课件主要包含了知识回顾，学习目标，课堂导入，新知探究，随堂练习，课堂小结，勾股定理，赵爽弦图，刘徽“青朱出入图”，加菲尔德总统拼图等内容，欢迎下载使用。

4.三角形内角和为180〫.
以下哪组数字可以构成三角形（ ）.A.2、3、5 B.2、2、4 C.2、5、5 D.3、4、7
解析：A.2+3=5，不满足
B.2+2=4，不满足
D.3+4=7，不满足
C.2+5>5，满足
判断三角形的三边关系只需要两边之和大于第三边.
1.探索并掌握勾股定理的证明过程.2.熟练运用勾股定理解决数学问题.
相传 2500 多年前，毕达哥拉斯有一次在朋友家作客时，发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.
请你观察一下地面的图案，从中发现了什么？
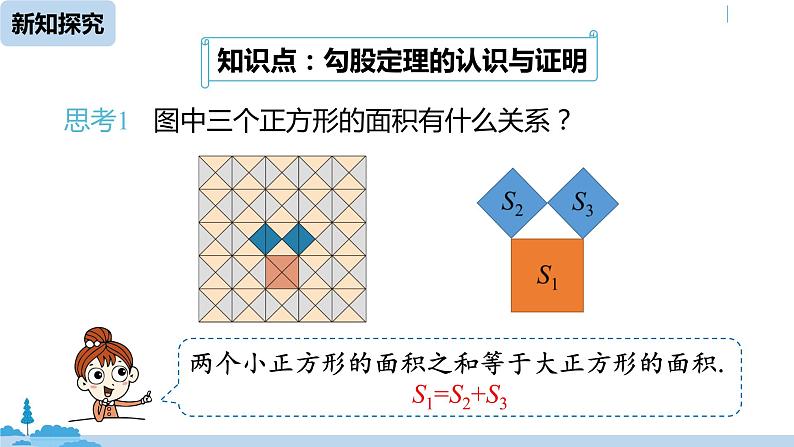
思考1 图中三个正方形的面积有什么关系？
两个小正方形的面积之和等于大正方形的面积.S1=S2+S3
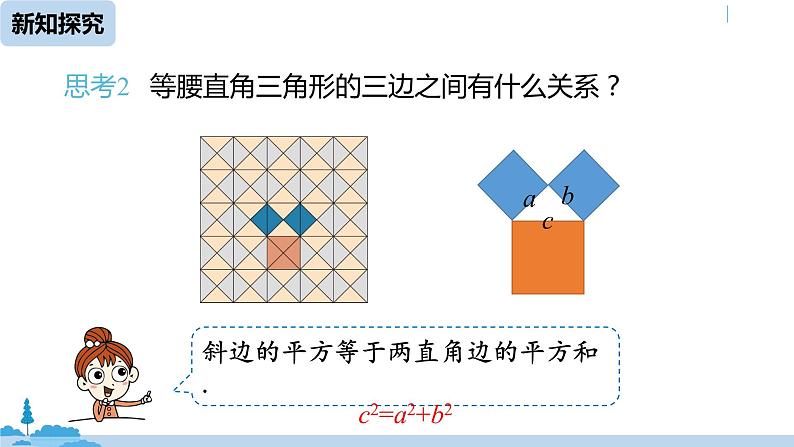
思考2 等腰直角三角形的三边之间有什么关系？
斜边的平方等于两直角边的平方和.c2=a2+b2
探究 等腰直角三角形有上述性质，其他的直角三角形也有这个性质吗？
如图，每个小方格的面积均为1，请分别算出图中正方形A、B、C、 A' 、 B' 、 C' 的面积，看看能得出什么结论？
通过上面的思考和探究，我们可以猜想：
证法一：赵爽弦图
边长分别为a、b的两个正方形分割成四个直角三角形和一个小正方形.
四个直角三角形和一个小正方形拼接成边长为c的大正方形.
证法二：加菲尔德总统拼图
如图，你能用两种方法计算梯形的面积S吗？
证法三：毕达哥拉斯拼图
分别计算左右两个正方形的面积，你能得出什么结论？
证法四：刘徽“青朱出入图”
1.勾股定理是直角三角形的特殊性质，所以其适用的前提是直角三角形.
2.运用勾股定理时，一定要分清直角边和斜边，若没有明确哪条边是斜边，则需要分类讨论，写出所有可能的情况，以避免漏解或者错解.
1.如图，图中所有的三角形都是直角三角形，四边形都是正方形.已知正方形 A、B、C、D 的边长分别为12、16、9、12，求最大正方形 E 的面积.
2.在直角三角形中，如果有两条边长为3、4，那么第三条边长为多少？
解：①已知两边都是直角边时，由勾股定理得：
②已知两边一条是直角边，一条是斜边时，由勾股定理得：
1.在Rt△ABC中，∠A、 ∠B、 ∠C的对边分别为a、b、c， ∠C=90〫.已知a：b=1 : 2，c=5，求b.
解：因为∠C=90〫， a：b=1:2，所以b=2a.
2.如图，每个小正方形的边长均为1，求三角形ABC的三边长.
3.已知直角三角形的两条边长为2、4，则第三条边长为多少？
解：（1）当2、4均为直角边时；
（2）当2为直角边，4为斜边时；
解析：因为 ∠B=90〫，所以b是斜边，a、c 是直角边.
2.某直角三角形一直角边长为3，另一直角边和斜边的和为9，求斜边的长为多少？
解：设斜边长为 x，则另一直角边长为 9- x.