





数学八年级下册19.3 正方形课文内容课件ppt
展开1.叙述平行四边形、矩形、菱形的定义和它们的特殊性质.2.说一说平行四边形、矩形、菱形的内在联系.
矩形的性质 矩形的四个角都是直角。
有一个角是直角的平行四边形是矩形。
有一组邻边相等的平行四边形叫做菱形。
菱形的性质 菱形的四条边都相等。
菱形的对角线互相垂直。
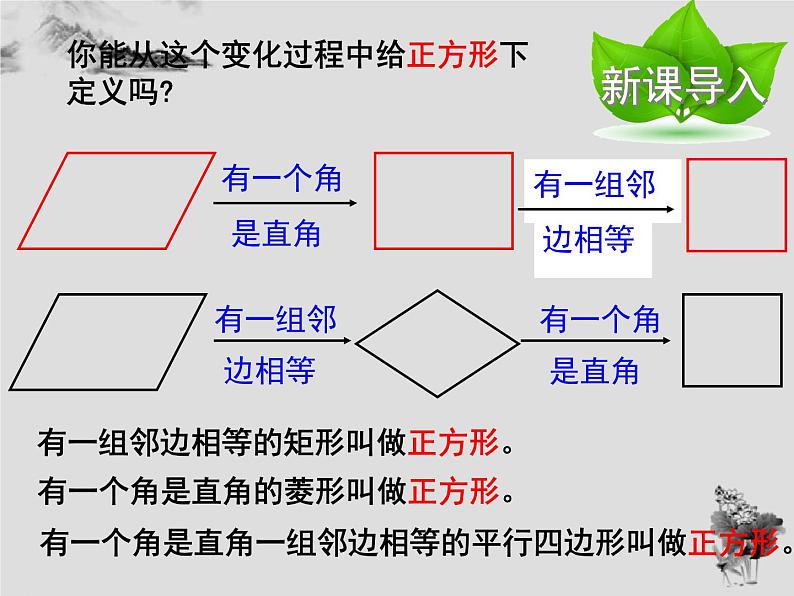
你能从这个变化过程中给正方形下定义吗?
有一个角是直角的菱形叫做正方形。
有一组邻边相等的矩形叫做正方形。
有一个角是直角一组邻边相等的平行四边形叫做正方形。
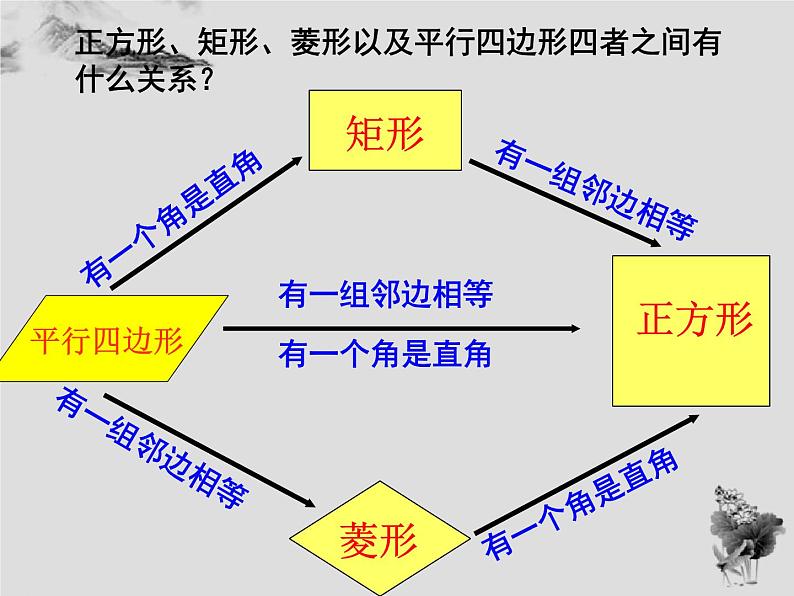
画图表示正方形与矩形、正方形与菱形的从属关系如下:
正方形、矩形、菱形以及平行四边形四者之间有什么关系?
(1)正方形是菱形吗?正方形具有哪些性质?
正方形是特殊的菱形,它具有平行四边形、矩形、菱形的一切性质。
边:对边平行,四边都相等。
对角线:对角线相等且互相垂直平分
(2)正方形是轴对称图形吗?如果是,它有几条对称轴?
正方形是轴对称图形,它有四条对称轴.即两条对角线,两组对边的中垂线.
对称:正方形既是轴对称图形,也是中心对称图形.
对边平行, 四条边都相等
四 个 角 都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形∴AC⊥BD,AC=BD,OA=OB=OC=OD, ∠1= ∠2= ∠3= ∠4= ∠5= ∠6= ∠7= ∠8
轴对称图形 中心对称图形
活动:四人一组进行讨论研究,通过分析与讨论,共同总结出判定一个四边形是正方形的基本方法.
(1)直接用正方形的定义判定,即先判定一个四边形是平行四边形,若这个平行四边形有一个角是直角,且有一组邻边相等,那么就可以判定这个平行四边形是正方形.
(2)先判定一个四边形是矩形,再判定这个矩形是菱形,那么这个四边形是正方形.(3)先判定一个四边形是菱形,再判定这个菱形是矩形,那么这个四边形是正方形.
后两种判定均要用到矩形和菱形的判定定理,矩形和菱形的判定定理是判定正方形的基础.
正方形的判定方法还可写成:有一个角是直角,且有一组邻边相等的平行四边形是正方形;有一组邻边相等的矩形是正方形;有一个角是直角的菱形是正方形.
(1)边长为2cm 的正方形,对角线的长是______cm
(2)正方形ABCD,对角线AC、BD相交于点O,问图中有____个等腰直角三角形
解:以正方形的四个顶点为直角顶点,共有四个等腰直角三角形,以正方形两条对角线的交点为顶点的等腰直角三角形也有四个,因而共有八个等腰直角三角形.
解: ∵正方形ABCD是菱形.
又 ∵正方形ABCD既是矩形又是菱形.
∴ ∠BAD=90°,且AC平分∠BAD
2如图,四边形ABCD是正方形,两条对角线相交于点O,求∠AOB,∠OAB的度数。
练习3:已知:如图,在正方形ABCD中,点 E在AC上.求证:BE=DE
证明:∵四边形ABCD 是正方形, ∴AB=AD, ∠BAC=∠DAC.
在△ABC和△ADC中 AB=AD ∠BAC=∠DAC. AE=AE ∴△ABC≌△ADC (SAS) ∴BE=DE (全等三角形的对应边相等)
练习4:正方形ABCD中,E是BC延长线上一点,且CE=AC, AE交DC于点F,试求∠E, ∠AFC的度数
∵四边形ABCD为正方形,
∵∠ACB是△ACE的一个外角
∴∠ACB=∠E+∠CAE=2∠E
∵∠AFC是△CEF的一个外角
∴∠AFC=∠E+∠FCE=22.5°+90°=112.5°
∴∠E=22.5°, ∠AFC=112.5°
判断下列命题是否正确:(1)正方形有四条对称轴;(2)正方形的两条对角线将其分成4个全等的等腰直角三角形;(3)对角线互相垂直的矩形是正方形;(4)对角线相等的菱形是正方形.
3.如图,将一张长方形纸对折两次,然后剪下一个角,打开,怎样才能剪出一个正方形?
只要保证剪口线与折痕成45°角即可
初中数学华师大版八年级下册19.3 正方形作业ppt课件: 这是一份初中数学华师大版八年级下册19.3 正方形作业ppt课件,共30页。
华师大版八年级下册19.3 正方形教课ppt课件: 这是一份华师大版八年级下册19.3 正方形教课ppt课件,共26页。PPT课件主要包含了学习目标,导入新课,情景引入,讲授新课,问题引入,正方形,问题发现,邻边相等,一个角是直角,正方形定义等内容,欢迎下载使用。
2020-2021学年19.3 正方形习题课件ppt: 这是一份2020-2021学年19.3 正方形习题课件ppt,共19页。













