初中数学华师大版八年级下册19.3 正方形作业ppt课件

这是一份初中数学华师大版八年级下册19.3 正方形作业ppt课件，共30页。

1. 正方形具有而菱形不具有的性质是 (　　)　　　　　 　　　　　　　　　　A.对角线互相平分 B.对角线相等C.对角线互相垂直 D.对角线平分对角
1.B　正方形的对角线互相垂直平分且相等,菱形的对角线互相垂直平分,故正方形具有而菱形不具有的性质是对角线相等.
2. [2021重庆沙坪坝区期中]如图,已知E是正方形ABCD对角线AC上一点,且AB=AE,则∠DBE的度数是 (　　)　　　　　 　　　　　　　　　　A.15°B.32.5°C.22.5° D.30°
2.C　∵AC,BD是正方形ABCD的对角线,∴∠BAE=∠ABD=45°.又∵AB=AE,∴∠ABE=∠AEB=67.5°,∴∠DBE=67.5°-45°=22.5°.
4.B　∵四边形PBEF为正方形,∴∠PBE=90°.∵∠CBE=α,∴∠PBC=90°-α.∵四边形APCD,PBEF是正方形,∴AP=CP,∠APF=∠CPB=90°,PF=PB,∴△APF≌△CPB,∴∠AFP=∠PBC=90°-α.
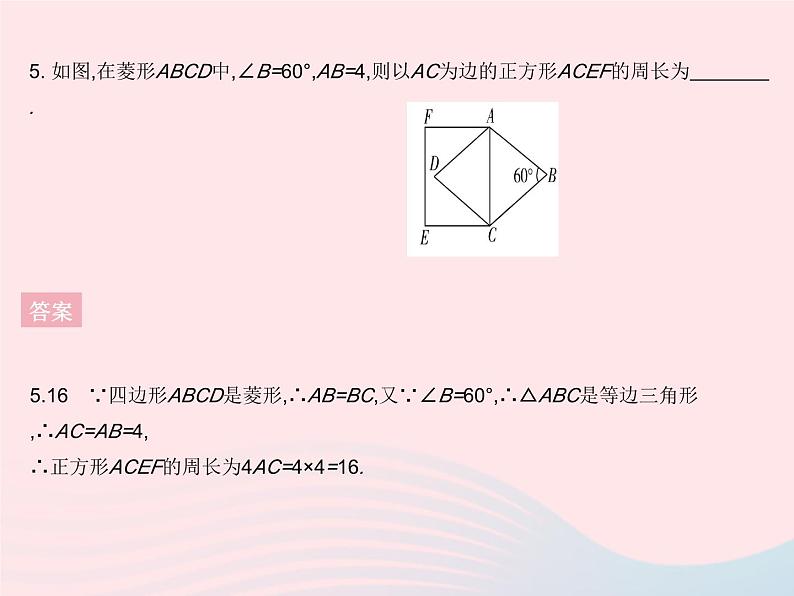
5. 如图,在菱形ABCD中,∠B=60°,AB=4,则以AC为边的正方形ACEF的周长为　　　　. 
5.16　∵四边形ABCD是菱形,∴AB=BC,又∵∠B=60°,∴△ABC是等边三角形,∴AC=AB=4,∴正方形ACEF的周长为4AC=4×4=16.
6. [教材P121习题T2变式]如图,四边形ABCD是正方形,点G是边BC上一点,DE⊥AG于点E,BF∥DE,且交AG于点F.已知DE=10,BF=6,则EF的长度为　　　　. 
6.4　∵四边形ABCD是正方形,∴AB=AD,∠BAF+∠DAE=∠BAD=90°,又∵DE⊥AG,BF∥DE,∴∠AED=∠BFA=90°,∴∠BAF+∠ABF=90°,∴∠ABF=∠DAE.在△DAE和△ABF中,∠AED=∠BFA,∠DAE=∠ABF,AD=BA,∴△DAE≌△ABF,∴AE=BF,AF=DE,∴EF=AF-AE=DE-BF=10-6=4.
8. [教材P124复习题T6变式]如图,四边形ABCD和四边形CEFG都是正方形.求证:(1)△BCG≌△DCE;(2)BG⊥DE.
8.证明:(1)∵四边形ABCD和四边形CEFG都是正方形,∴BC=DC,CE=CG,∠BCD=∠GCE=90°,∴∠BCG=∠DCE.在△BCG和△DCE中,BC=DC,∠BCG=∠DCE,CG=CE,∴△BCG≌△DCE.(2)设BG分别与DC,DE交于点H,O.∵△BCG≌△DCE,∴∠HBC=∠ODH.∵∠BHC=∠DHO,∠HBC+∠BHC=90°,∴∠ODH+∠DHO=90°,∴∠DOH=90°,∴BG⊥DE.
9. 如图1,正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM与BD相交于点F.(1)求证:OE=OF.(2)如图2,若点E在AC的延长线上,AM⊥BE交EB的延长线于点M,延长AM交DB的延长线于点F,其他条件不变,结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
4. 如图,点P是正方形ABCD的边AB上一点(不与A,B重合),连接PD,并将线段PD绕点P顺时针旋转90°得到线段PE,连接BE,则∠CBE等于 (　　)A.75°B.60°C.45°D.30°
4.C　如图,过点E作EF⊥AB,交AB的延长线于点F,则∠F=90°.∵线段PE是线段PD绕点P顺时针旋转90°得到的,∴PD=PE,∠DPE=90°,∴∠APD+∠EPF=90°.在正方形ABCD中,AD=AB,∠A=∠ABC=90°,∴∠APD+∠ADP=90°,∴∠ADP=∠EPF.在△APD和△FEP中,∠ADP=∠FPE,∠A=∠F=90°,PD=EP,∴△APD≌△FEP,∴AP=FE,AD=FP.又∵AD=AB,∴AB=PF,∴AP+PB=PB+BF,∴AP=BF,∴BF=EF.又∵∠F=90°,∴△BEF为等腰直角三角形,∴∠EBF=45°,又∵∠CBF=∠ABC=90°,∴∠CBE=90°-45°=45°.
5. 如图,正方形ABCD中,E,F是对角线BD上的两点,BD=6,BE=DF=4,则四边形AECF的面积为　　　　. 
6. 易错题 如图,在正方形ABCD中,点E在边DC上,DE=3,EC=1,连接AE.若点F在射线AB上,且满足CF=AE,则A,F两点间的距离为　　　　. 
6.1或7　∵DE=3,EC=1,∴正方形ABCD的边长为4.在Rt△ADE和Rt△CBF中,AE=CF,AD=CB,∴Rt△ADE≌Rt△CBF,∴BF=DE=3.∵点F在射线AB上,∴分两种情况:①当点F在线段AB上时,AF=AB-BF=4-3=1;②当点F在线段AB的延长线上时,AF=AB+BF=4+3=7.综上,A,F两点间的距离为1或7.
7. [2020江苏淮安清江浦区期末]如图,已知正方形ABCD,E是AD上一点,过BE上一点O作BE的垂线,交AB于点G,交CD于点H.若BE=6,则GH=　　　　. 
7.6　如图,过点A作GH的平行线,交DC于点H',交BE于点O'.∵四边形ABCD是正方形,∴AG∥H'H,BA=AD,∠BAE=∠D=90°,∴∠H'AD+∠AH'D=90°.∵GH⊥BE,AH'∥GH,∴AH'⊥BE,∴∠H'AD+∠BEA=90°,∴∠BEA=∠AH'D.在△BAE和△ADH'中,∵∠BAE=∠D,∠BEA=∠AH'D,BA=AD,∴△BAE≌△ADH',∴BE=AH'.∵AG∥H'H,AH'∥GH,∴四边形AH'HG是平行四边形,∴GH=AH',∴GH=BE=6.
8. 如图,正方形ABCD的边长为1,P,Q分别为边AB,AD上的点,△APQ的周长为2,连接PC.求证:(1)PB+QD=PQ;(2)∠BPC=∠QPC.
9. 如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.(1)请判断:FG与CE的数量关系是　　　　,位置关系是　　　　. (2)如图2,若点E,F分别是CB,BA延长线上的点,其他条件不变,(1)中结论是否仍然成立?请作出判断并给予证明.(3)如图3,若点E,F分别是BC,AB延长线上的点,其他条件不变,(1)中结论是否仍然成立?请直接写出你的判断.