湘教版九年级下册2.7 正多边形与圆图文ppt课件

这是一份湘教版九年级下册2.7 正多边形与圆图文ppt课件，共16页。PPT课件主要包含了知识探究，知识点❶，正多边形的定义，四边不相等，四角不相等，正多边形，各边相等，各角相等，缺一不可，知识点❷等内容，欢迎下载使用。

观察下面多边形，它们的边、角有什么特点？
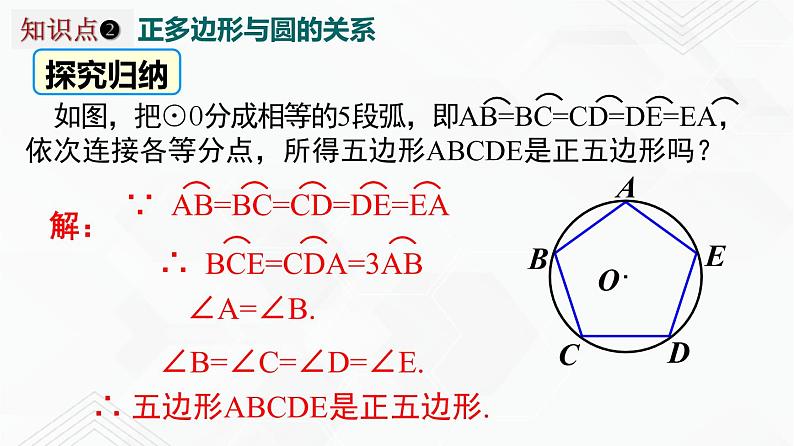
它们的各边都相等，各内角也相等.
各边相等，各内角也相等的多边形叫做正多边形.如果一个正多边形有n(n≥3)条边，那么这个正多边形叫做正n边形.
矩形ABCD是正四边形吗？为什么？
菱形ABCD是正四边形吗？为什么？
∠B=∠C=∠D=∠E.
∴ 五边形ABCDE是正五边形.
弦相等（多边形的边相等） 圆周角相等（多边形的角相等）
将圆n(n≥3)等分，依次连接各等分点，所得到的多边形是正多边形吗？
将一个圆n(n≥3)等分，依次连接各等分点所得到的多边形叫作这个圆的内接正多边形，这个圆是这个正多边形的外接圆，正n边形的各顶点n等分其外接圆.
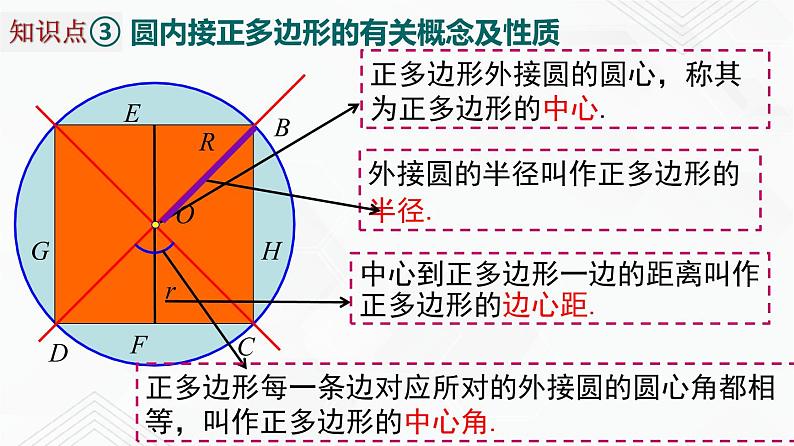
圆内接正多边形的有关概念及性质
正多边形外接圆的圆心，称其为正多边形的中心.
外接圆的半径叫作正多边形的半径.
中心到正多边形一边的距离叫作正多边形的边心距.
正多边形每一条边对应所对的外接圆的圆心角都相等，叫作正多边形的中心角.
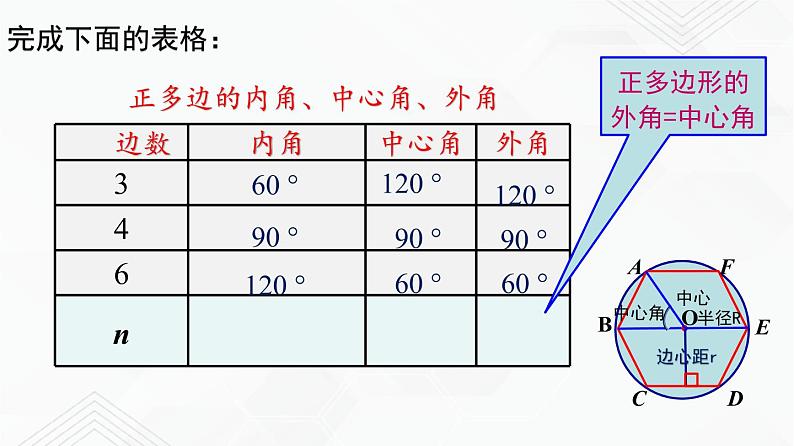
正多边形的外角=中心角
正多边的内角、中心角、外角
圆内接正多边形的有关计算
正n边形的边长a，半径R，边心距r之间关系
边长a，边心距r的正n边形的面积
例1 有一个亭子,它的地基是半径为4 m的正六边形,求地基的周长和面积 (精确到0.1 m2).
解：过点O作OM⊥BC于M.连结OB、OC
亭子地基的周长l=6×4=24(m)
利用勾股定理,可得边心距
2.作边心距，构造直角三角形.
圆内接正多边形的辅助线
1.如图，正方形ABCD是⊙O的内接正方形，点P是劣弧CD上不同于点C的任意一点，则∠BPC的度数是________度．
2.如图，正八边形ABCDEFGH的半径为2，它的面积为_____．
只要将一个圆n等分，就可以得到正n边形.
将圆心角n等分，就可以将圆n等分.
例2 已知⊙O的半径为r，求作⊙O的内接正六边形.
作法：（1）在⊙O上以任意一点A为圆心、以r为半径画弧，连续截取点B、C、D、E、F； （2）依次连接AB、BC、CD、DE、EF、FA，则六边形ABCDEF即为所求.
分析：因为正六边形每条边所对的圆心角为 __ ，所以正六边形的边长与圆的半径 _ .因此，在半径为r的圆上依次截取等于 的弦，即可将圆六等分.
正三角形、正方形、正五边形、正六边形是否为轴对称图形？如果是轴对称图形，试画它们所有的对称轴.
1.正n边形 __ 轴对称图形，共有 __ 条对称轴；2.n为奇数时，n条对称轴过中心与 ___； (如上图中蓝色直线)3.n为为偶数时，n条对称轴中： n/2条过中心与 __ ； (如上图中蓝色直线) n/2条过中心与边的 ___ 点. (如上图中红色直线)
下列正多边形中哪些是中心对称图形？哪些是旋转对称图形？
如果是旋转对称图形，绕中心最少旋转多少度所得图形与原图形重合？
2. 若正多边形的边心距与半径的比为1:2，则这个多边形的边数 .
3.已知一个正多边形的每个内角均为108°，则它的中心角为___度．
4.下列说法正确的是（ ）A.各边都相等的多边形是正多边形 B.一个圆有且只有一个内接正多边形C.圆内接正四边形的边长等于半径 D.圆内接正n边形的中心角度数为