
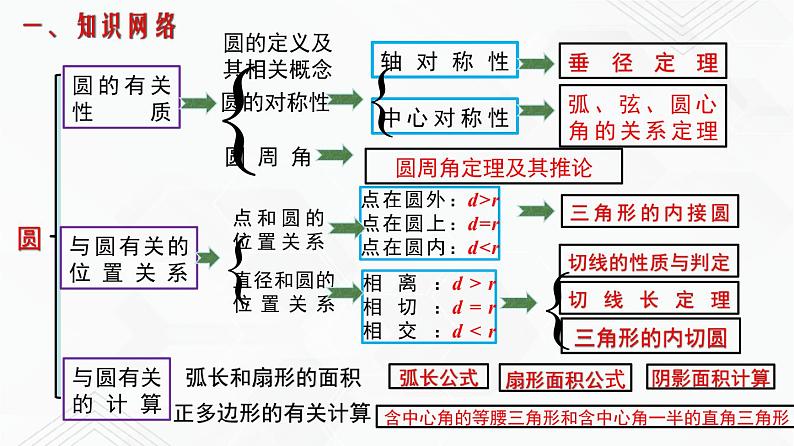


初中湘教版第2章 圆综合与测试复习课件ppt
展开弧、弦、圆心角的关系定理
点在圆外:d>r点在圆上:d=r 点在圆内:d
一、圆的定义及其相关概念
1、圆的定义:平面内到一定点的距离等于定长的所有点组成的图形叫做圆
圆也可以看成是一个动点绕一个定点旋转一周所形成的图形..
这个定点叫作圆心(O),
定点O与动点A的连线段叫作半径.OA
以点O为圆心的圆叫作圆O,记作⊙O
连接圆上任意两点的线段叫做弦.
经过圆心的弦叫做直径.
直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
圆上任意两点间的部分叫做圆弧,简称弧,弧用符号“⌒”表示.
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
小于半圆的弧叫做劣弧.
大于半圆的弧叫做优弧.
能够完全重合的圆或半径相等的圆是等圆
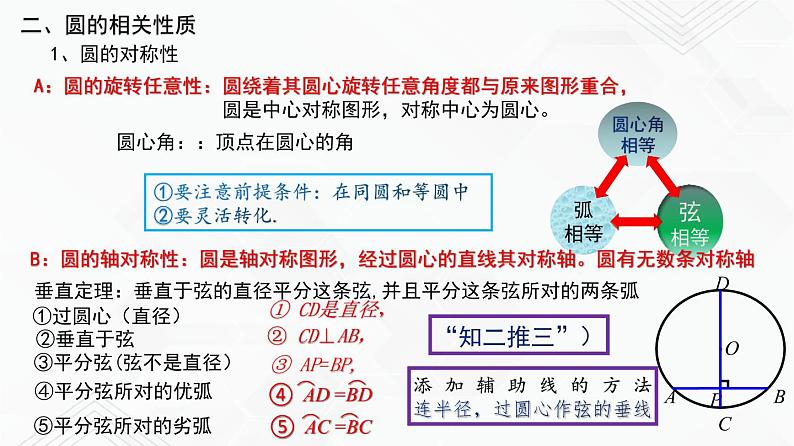
A:圆的旋转任意性:圆绕着其圆心旋转任意角度都与原来图形重合, 圆是中心对称图形,对称中心为圆心。
圆心角::顶点在圆心的角
①要注意前提条件:在同圆和等圆中②要灵活转化.
B:圆的轴对称性:圆是轴对称图形,经过圆心的直线其对称轴。圆有无数条对称轴
垂直定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧
③平分弦(弦不是直径)
添加辅助线的方法连半径,过圆心作弦的垂线
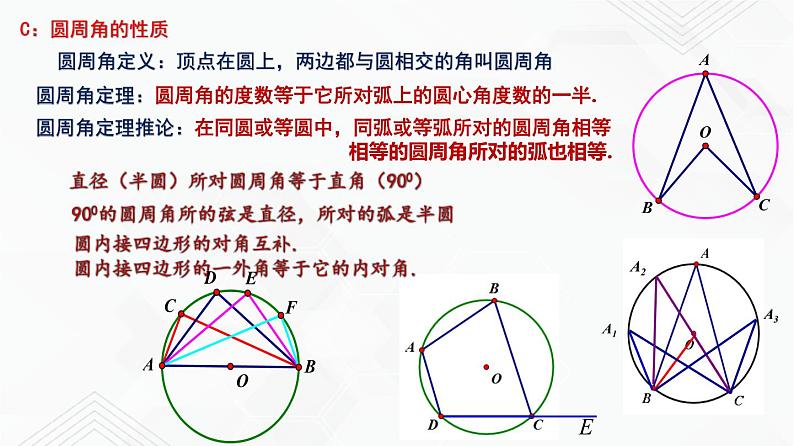
圆周角定义:顶点在圆上,两边都与圆相交的角叫圆周角
圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半.
圆周角定理推论:在同圆或等圆中,同弧或等弧所对的圆周角相等 相等的圆周角所对的弧也相等.
直径(半圆)所对圆周角等于直角(900)
900的圆周角所的弦是直径,所对的弧是半圆
圆内接四边形的一外角等于它的内对角.
圆内接四边形的对角互补.
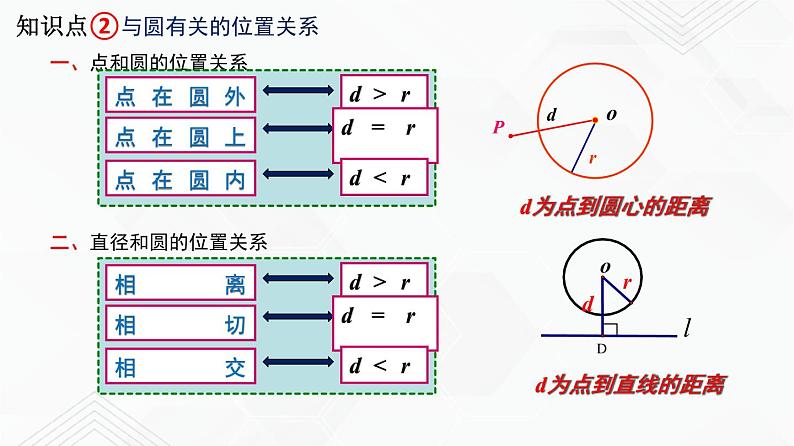
知识点②与圆有关的位置关系
二、直径和圆的位置关系
直线与圆只有1个公共点
圆心到切线的距离等于半径即d=r
圆的切线垂直于经过切点的半径
有切线时常用辅助线添加方法 见切线,连切点圆心,得垂直.
圆心到直线的距离等于半径即d=r
直线经过半径外端点且垂直于这条半径
证切线时常用辅助线添加方法 ①有公共点,连半径,证垂直②无公共点,作垂直,证半径.
过圆外一点所画的圆的两条切线长相等,圆心和这一点的连线平分两条切线的夹角.
常用辅助线添加方法 ①分别连接圆心和切点②连接两切点③连接圆心和圆外一点.
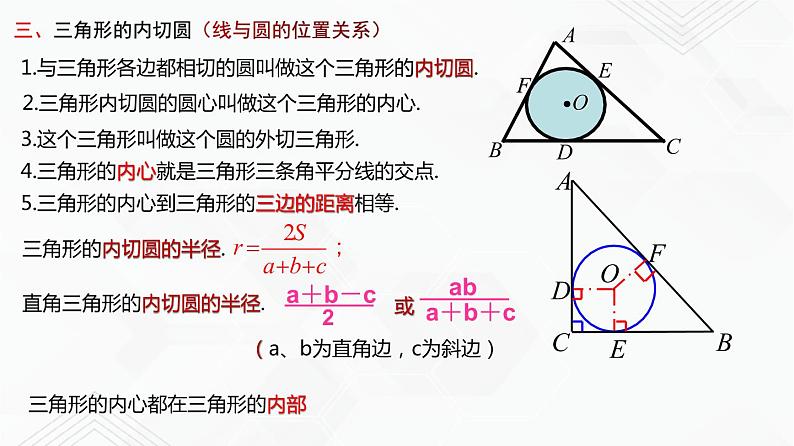
三、三角形的内切圆(线与圆的位置关系)
1.与三角形各边都相切的圆叫做这个三角形的内切圆.
2.三角形内切圆的圆心叫做这个三角形的内心.
3.这个三角形叫做这个圆的外切三角形.
4.三角形的内心就是三角形三条角平分线的交点.
5.三角形的内心到三角形的三边的距离相等.
三角形的内切圆的半径.
直角三角形的内切圆的半径.
(a、b为直角边,c为斜边)
三角形的内心都在三角形的内部
四、三角形的外接圆(点与圆的位置关系)
1、经过一个三角形各个顶点的圆叫做这个三角形的外接圆
2、外接圆的圆心叫做这个三角形的外心
3、这个三角形叫做圆的内接三角形
4、外心是△ABC三条边的垂直平分线的交点
5、外心到三角形的三个顶点的距离相等.
锐角三角形直角三角形 --外心的位置--钝角三角形
知识点③与圆有关的计算
整体思想:化不规则为规则
添加辅助线的方法连半径,作边心距
转化为直角三角形有关计算
知识点① 圆的有关概念和性质
1.如图,AB是☉O的直径,点C,D,E在☉O上,若∠AED=20°,则∠BCD的度数为( )
A. 72° B.54° C. 45° D.36 °
2.如图,四边形ABCD为⊙O的内接正方形,点P为劣弧BC上的任意一点(不与B,C重合),则∠BPC的度数是 .
3.如图,线段AB是直径,点D是⊙O上一点, ∠CDB=20 °,过点C作⊙O的切线交AB的延长线于点E,则∠E等于 .
4.如图,C是扇形OAB上AB一点,OA=2,且∠AOB=90 °连接AC,BC,过点O作OE ⊥AC,OF ⊥BC,垂足分别为E,F,连接EF,则EF的长度等于 .5.如图,AB是⊙O的直径,且AB=2,C,D是同一半圆上的两点,并且AC与BD的度数分别是96 °和36 °,动点P是AB上的任意一点,则PC+PD的最小值是 .
6. 如图, ⊙O的直径AE=4cm, ∠B=30 °,则AC= .
7.如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上任意一点(不与点A,B重合),连接CO并延长CO交⊙O于点D,连接AD.则弦长AB=________(结果保留根号).
当∠D=20°时,则∠BOD= .
8.弦AB所对的圆心角是60°,则弦AB所对的圆周角的度数为( )(A)60° (B)120° (C)30°或150° (D)60°或120°9.如图,A,B,C是☉O上的三点,且四边形OABC是菱形.若点D是圆上异于A,B,C的另一点,则∠ADC的度数是 .
10.已知半径为2的☉O中,弦AC=2,弦AD=2 ,则∠COD的度数为 ,
11.如图,AB是⊙O的直径,弦BC=2,F是弦BC的中点, ∠ABC=60 °.若动点E以2cm/s的速度从A点出发沿着A→B →A的方向运动,设运动时间为t(s) (0
2、如图,已知直线AD是☉O的切线,点A为切点,OD交☉O于点B,点C在☉O上,且∠ODA=36°,则∠ACB的度数为( )
(A)54° (B)36° (C)30° (D)27°
3、如图,AB是☉O的直径,PA切☉O于点A,连接PO并延长交☉O于点C,连接AC,AB=10,∠P=30°,则AC的长度是( )
4、如图,直线AB,CD相交于点O, ∠AOD=30 °,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么 秒钟后⊙P与直线CD相切.
(1)求证:DE是☉O的切线;
5、如图,已知⊙O的直径AB=12,弦AC=10,D是BC弧的中点,过D作DE⊥AC交AC的延长线于E。
解:过O作OF⊥AC于,连结OC.
∴四边形ODEF为矩形
∵OF⊥AC,OF边圆心
∴AE=AF+EF=6+5=11
6、如图, O为正方形对角线上一点,以点O 为圆心,OA长为半径 的⊙O与BC相切于点M. (1)求证:CD与⊙O相切; (2)若正方形ABCD的边长为1,求⊙O的半径.
(1)证明:过点O作ON⊥CD于N.连接OM ∵BC与⊙O相切于点M, ∴ ∠OMC=90 °, ∵四边形ABCD是正方形,点O在AC上.∴AC是∠BCD的角平分线,∴ON=OM,∴ CD与⊙O相切.
方法总结 A、证切线时添加辅助线的解题方法有两种: ①有公共点,连半径,证垂直; ②无公共点,作垂直,证半径;B、有切线时添加辅助线的解题方法是:见切点,连半径,得垂直;设了未知数,通常利用勾股定理建立方程.
7、如图,⊙O是△ABC的外接圆,FH是⊙O 的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.(1)证明:AF平分∠BAC;(2)证明:BF=FD;(3)若EF=4,DE=3,求AD的长.
证明:(1)连结OF ∵FH是⊙O的切线 ∴OF⊥FH ∵FH∥BC , ∴OF垂直平分BC
∴AF平分∠BAC
(2)证明:由(1)及题设条件可知∠1=∠2,∠4=∠3,∠5=∠2 ∴∠1+∠4=∠2+∠3 ∴∠1+∠4=∠5+∠3 ∠FDB=∠FBD∴BF=FD
(3)解: 在△BFE和△AFB中∵∠5=∠2=∠1,∠F=∠F∴△BFE∽△AFB ∴
知识点③与圆有关的计算
1、一条弧所对的圆心角为135 ° ,弧长等于半径为5cm的圆的周长的3倍,则这条弧的半径为 .
2、正六边形的边长为8 cm,则它的面积为 cm2.
3.如图,点D在☉O的直径AB的延长线上,点C在☉O上,AC=CD,∠ACD=120°.
若☉O的半径为2,求图中阴影部分的面积.
求证:CD是☉O的切线;
4、若正方形的边长为6,则其外接圆与与内切圆组成的圆环的面积是 (结果保留π).
5、如图,正方形ABCD边长为4,以BC为直径的半圆O交对角线BD于E.则直线CD与⊙O的位置关系是 ,阴影部分面积为 (结果保留π) .
6、如图,已知正方形的边长为2cm,以对角的两个顶点为圆心,2cm,长为半径画弧,则所得到的两条弧的长度之和为 (结果保留π)
湘教版九年级下册第3章 投影与视图3.3 三视图图片ppt课件: 这是一份湘教版九年级下册第3章 投影与视图3.3 三视图图片ppt课件,共21页。PPT课件主要包含了主视方向,画出正三棱柱的三视图,画出下列物体的三视图,主视图,左视图等内容,欢迎下载使用。
初中数学湘教版九年级下册3.1 投影备课课件ppt: 这是一份初中数学湘教版九年级下册3.1 投影备课课件ppt,共20页。PPT课件主要包含了知识点❶投影的概念,照射光线叫做投影线,投影线,投影面,练一练,平行投影,中心投影,平行投影和中心投影,A3B3,点A3B3等内容,欢迎下载使用。
湘教版九年级下册2.7 正多边形与圆图文ppt课件: 这是一份湘教版九年级下册2.7 正多边形与圆图文ppt课件,共16页。PPT课件主要包含了知识探究,知识点❶,正多边形的定义,四边不相等,四角不相等,正多边形,各边相等,各角相等,缺一不可,知识点❷等内容,欢迎下载使用。














