初中数学湘教版九年级下册2.7 正多边形与圆示范课课件ppt

这是一份初中数学湘教版九年级下册2.7 正多边形与圆示范课课件ppt，共17页。PPT课件主要包含了正多边形定义，教材P84页，轴对称，中心对称图形，教材P85页，教材P86页，随堂练习等内容，欢迎下载使用。

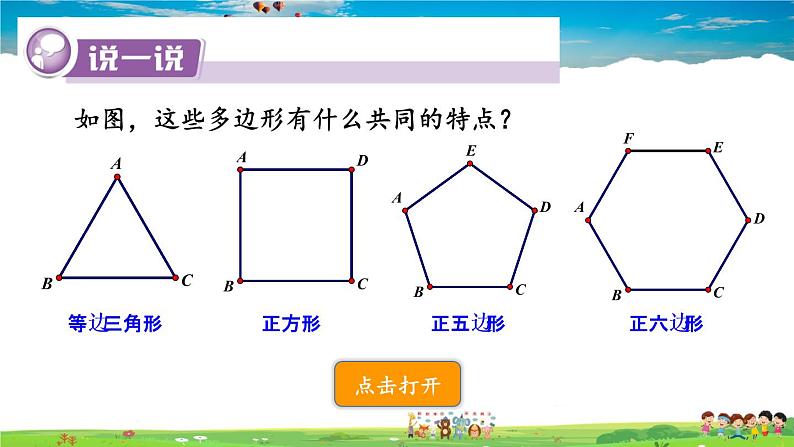
如图，这些多边形有什么共同的特点？
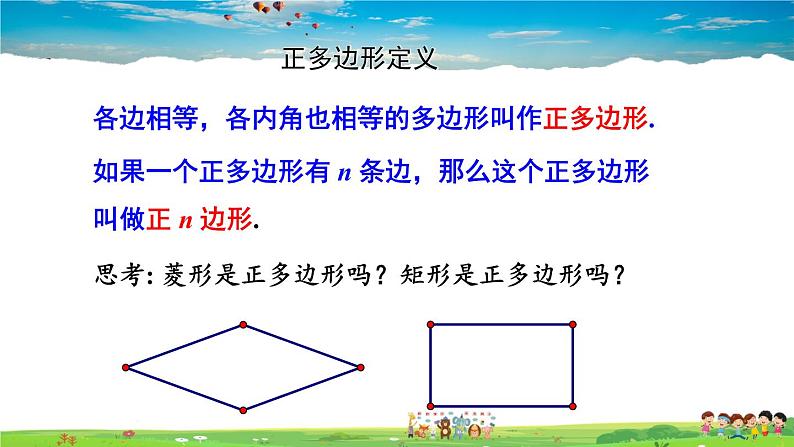
各边相等，各内角也相等的多边形叫作正多边形.
如果一个正多边形有 n 条边，那么这个正多边形叫做正 n 边形.
思考: 菱形是正多边形吗？矩形是正多边形吗？
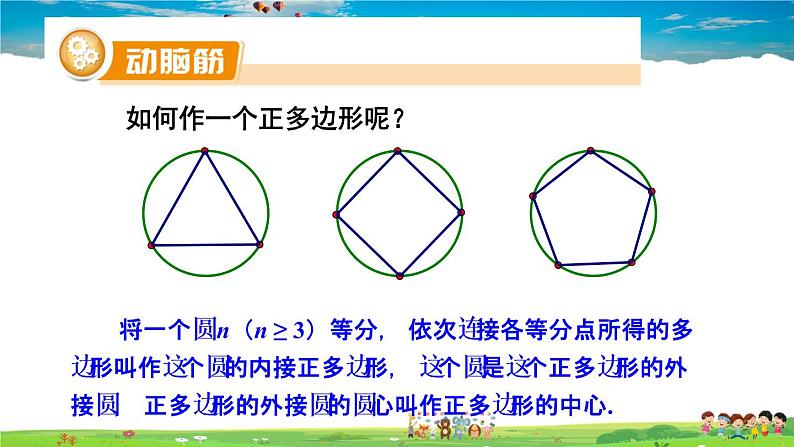
如何作一个正多边形呢？
将一个圆 n（n ≥ 3）等分， 依次连接各等分点所得的多边形叫作这个圆的内接正多边形， 这个圆是这个正多边形的外接圆， 正多边形的外接圆的圆心叫作正多边形的中心.
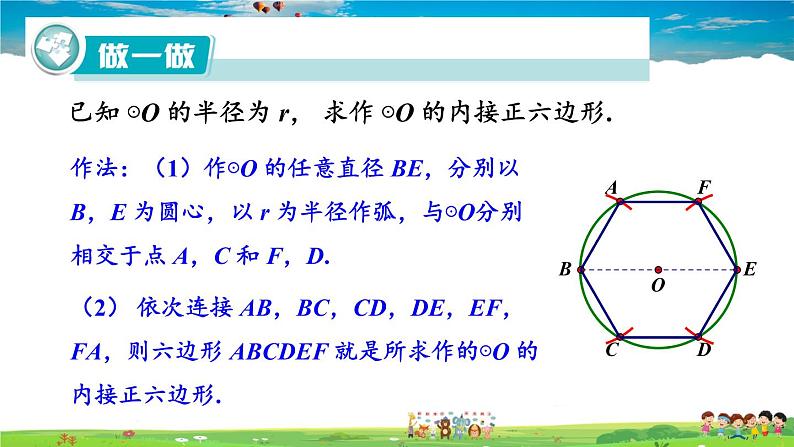
已知 ⊙O 的半径为 r， 求作 ⊙O 的内接正六边形.
作法：（1）作⊙O 的任意直径 BE，分别以 B，E 为圆心，以 r 为半径作弧，与⊙O分别相交于点 A，C 和 F，D.
（2） 依次连接 AB，BC，CD，DE，EF， FA，则六边形 ABCDEF 就是所求作的⊙O 的内接正六边形.
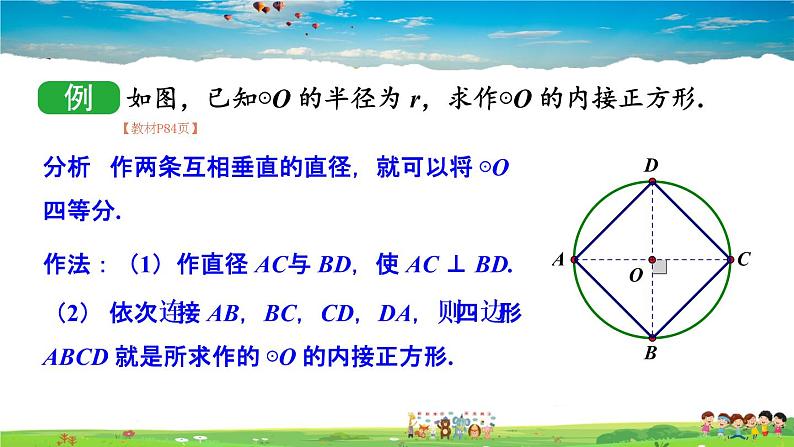
如图，已知⊙O 的半径为 r，求作⊙O 的内接正方形.
分析 作两条互相垂直的直径，就可以将 ⊙O 四等分.
作法：（1）作直径 AC与 BD，使 AC ⊥ BD.
（2） 依次连接 AB，BC，CD，DA，则四边形 ABCD 就是所求作的 ⊙O 的内接正方形.
在生产设计中，人们经常会遇到等分圆的问题. 例如设计剪纸、齿轮、汽车轮毂等就是通过等分圆而得到的.
观察图中的正多边形，哪些是轴对称图形？哪些是中心对称图形？如果是轴对称图形，画出其对称轴； 如果是中心对称图形，找出其对称中心.
正多边形都是 图形,一个正 n 边形共有 条对称轴，每条对称轴都通过 n 边形的 .
边数是偶数的正多边形还是 ，它的中心就是对称中心.
已知⊙O 的半径为 2 cm， 求作⊙O 的内接正方形和内接正六边形.
2. 许多图案设计都和圆有关，观察下图，请利用等分圆 的方法设计一幅图案.
1. 对于一个正多边形,下列四个命题中, 错误的是（ ） A. 正多边形是轴对称图形, 每条边的垂直平分线是它的对称轴 B. 正多边形是中心对称图形, 正多边形的中心是它的对称中心 C. 正多边形每一个外角都等于正多边形的中心角 D. 正多边形每一个内角都与正多边形的中心角互补
2. 如图, 平面上两个正方形与正五边形都有一条公共边, 则∠α 等于（ ） A. 45° B. 56° C. 60° D. 72°
3. （贵阳中考）如图, 正六边形 ABCDEF 内接于☉O, ☉O 的半径为 6, OM ⊥ BC 于点 M , 则 OM 的长为 _______．