



初中数学沪科版八年级下册18.1 勾股定理获奖课件ppt
展开和另外两边的关系时,
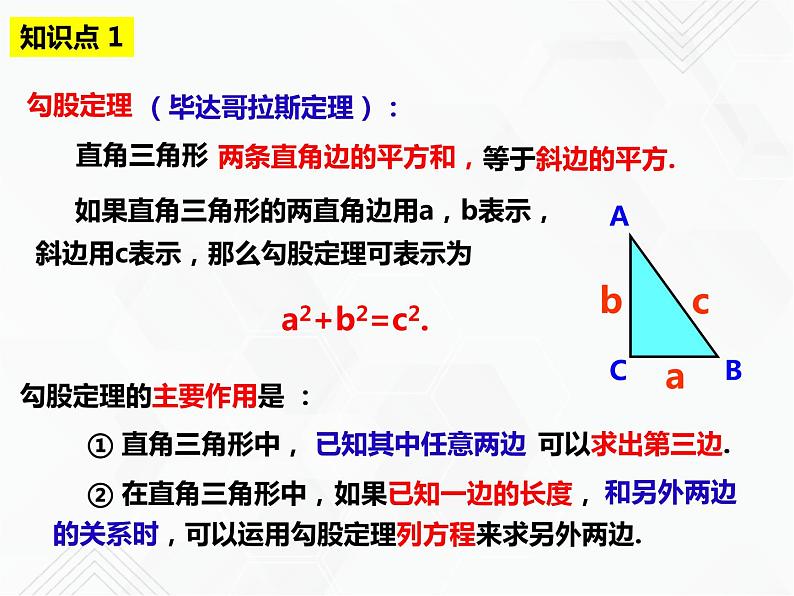
如果直角三角形的两直角边用a,b表示,斜边用c表示,那么勾股定理可表示为
勾股定理的主要作用是 :
可以运用勾股定理列方程来求另外两边.
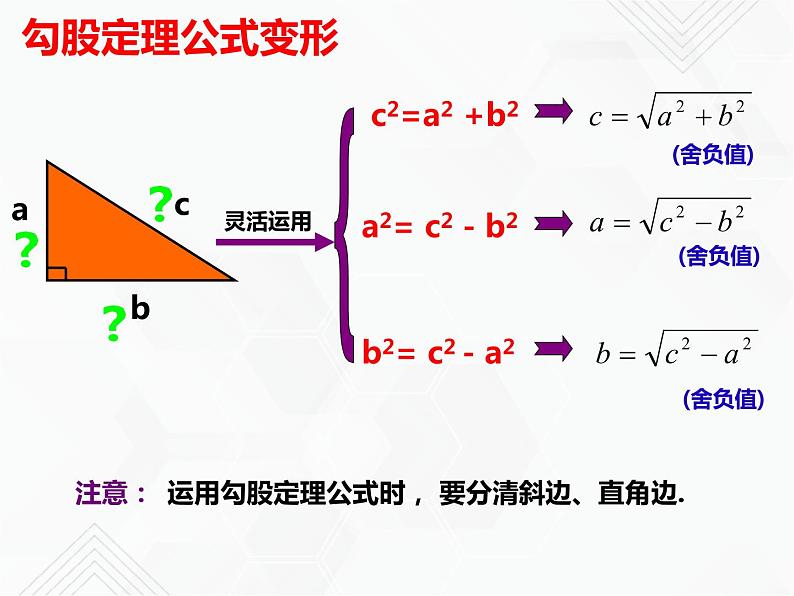
b2= c2 - a2
a2= c2 - b2
1、在△ABC中,∠C=90°,AB=c,BC=a,AC=b.
(1) a=6,b=8,求 c;
(2) a=8,c=17,求 b;
(1) ∵ ∠C=90°,a=6,b=8
(2) ∵ ∠C=90°,a=8,c=17
2、小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗?
解:设旗杆AC的高度为 x 米,
则绳子AB的长为 (x+1) 米.
x2+52=(x+1)2
答:旗杆的高度为12米.
如果已知一边的长度,
注意:在直角三角形中,
可以运用勾股定理列方程来求另外两边.
那么这个三角形是直角三角形.
那么这个三角形是直角三角形.
a2 + b2 = c2,
如果三角形的三边长a、b、c满足
∴ △ABC是直角三角形,
∵ 在△ABC中, a2+b2=c2
只要看两条较小边的平方和
判断三角形是不是直角三角形,
1、已知:在△ABC中,三条边长分别为 a=n2-1,b=2n,c=n2+1 (n>1) . 求证: △ABC为直角三角形.
∴ △ABC是直角三角形
(n2-1)2+(2n)2
=n4-2n2+1+4n2
2、已知:如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积?
∵ ∠B=90°,AB=3,BC=4
又∵ CD=12,AD=13
AC2+CD2=AD2
∴ △ACD是直角三角形,
∴ S四边形ABCD =
∴ 四边形ABCD的面积是36.
但直角三角形的三边长
(2)勾股数必能成为直角三角形的三条边长,
(1) 勾股数必须同时满足
① 三个数都是正整数.
② 两个较小数的平方和等于最大数的平方.
(3) 如果 a,b,c是一组勾股数,
那么 na,nb,nc
你能写出常用的勾股数吗?
3,4,5;
1、已知直角三角形的两边长分别为6,8,求第三条边的长.
(1) 当直角边为6和8时,
(2) 当斜边长为8时,
2、在△ABC中,AB=20,AC=15,AD为BC边上的高,且AD=12,求△ABC的周长.
① 当△ABC是锐角三角形时,
∵ 在Rt△ABD中,
AB=20,AD=12
又∵ 在Rt△ADC中,
AC=15,AD=12
② 当△ABC是钝角三角形时,
综上所述:△ABC的周长为
3.已知Rt△ABC中,∠C=90°,若a +b=14,c=10,求△ABC的面积.
∴ (a+b)2=196
又∵ 在Rt△ABC中,c=10
(a+b)2-(a2+b2)
4、如图所示,已知△ABC中,∠ACB=90°,AB=5cm,BC=3cm,CD⊥AB于D,求CD的长.
解:∵ 在 Rt△ABC 中,∠ACB=90°, AB=5cm,BC=3cm
又∵ Rt△ABC的面积
变式练习 如图,在正方形网格中,小正方形的边长为1,点A,B,C为各点(格子线的交点).
(1) 判断△ABC的形状,并说明理由;
(2) 求AB边上的高;
BC2+AC2=AB2
△ABC是直角三角形
又∵ Rt△ABC的面积
5、如图,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示.证明 S1=S2+S3 .
变式一:如图,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,那么S1、S2、S3之间有什么关系?(不必证明)
变式二:如图③,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1、S2、S3之间的关系并加以证明;
变式三: 若分别以直角三角形ABC三边为边向外作三个正多边形,其面积分别用S1、S2、S3表示,请你猜想S1、S2、S3之间的关系?.
分别以直角三角形三边为边向外作三个正多边形,
就等于斜边上的图形的面积.
直角边上的图形的面积之和
即 S1=S2+S3
6、 求图中字母所代表的正方形的面积。
变式练习 如图,直线上有三个正方形a,b,c,若a、c的面积分别为5和11,求b的面积
变式练习 在直线 l 上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个的正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4= 。
另两边可通过重合图形找到数量关系,
这个直角三角形一般已知一边,
其解题步骤为:
要紧扣折叠前后的对应边,对应角相等,
7、如图,小颍同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
① 利用重合的图形传递数据
便能利用勾股定理列方程求解.
8、 如图,有一块直角三角形纸片,两直角边AB=6cm,BC=8cm,现将三角形纸片沿直线AD折叠,使点B落在AC上,与点E重合,求DE的长度.
9、矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕EF的长.
10. 如图,一架梯子长25m,斜靠在一面墙上,梯子底端离墙 7m.
(1) 这个梯子的顶端距地面有多高?
(2) 如果梯子的顶端下滑了4m,那么梯子的底端在水平方向上滑动了几米?
则梯子的底端水平滑动距离也为 xm.
(3) 当梯子的顶端下滑的距离与梯子的底端水平滑动距离相等时,这时梯子的顶端距离地面有多高?
设梯子的顶端下滑的距离为 x m,
∴ 梯子的顶端下滑的距离为17米
∴ 梯子顶端距离地面的高度为
11、高速公路的同一侧有A,B两城镇,如图,它们到高速公路所在直线MN的距离分别为AA'=2km,BB'=4km,A'B'=8km.要在高速公路上A',B'之间建一个出口P,使A,B两城镇到P的距离之和最短.求这个最短距离.
则△CBD为直角三角形.
∵ AA'=2km,BB'=4km,A'B'=8km.
∴ 在Rt△CBD中,
作点A关于MN的对称点C,
则点P即为出口的位置.
过点C作CD⊥BB',
交BB'的延长线于点D,
12、如图,点P为正方形ABCD内一点,且 PA:PB:PC=1:2:3,求∠APB的度数.
13、如图,公路MN和小路PQ在P处交汇,∠QPN=30°,点A处有一所学校,AP=160m,假设拖拉机行使时,周围100m内受噪音影响,那么拖拉机在公路MN上以18km/h的速度沿PN方向行驶时,学校是否受到噪音的影响?如果学校受到影响,那么受影响将持续多长时间?
初中数学沪科版八年级下册18.1 勾股定理作业ppt课件: 这是一份初中数学沪科版八年级下册18.1 勾股定理作业ppt课件,共20页。
初中数学沪科版八年级下册18.1 勾股定理作业课件ppt: 这是一份初中数学沪科版八年级下册18.1 勾股定理作业课件ppt,共41页。
初中数学沪科版八年级下册18.1 勾股定理习题课件ppt: 这是一份初中数学沪科版八年级下册18.1 勾股定理习题课件ppt,共17页。PPT课件主要包含了答案呈现,习题链接,a2+b2=c2等内容,欢迎下载使用。













