数学八年级下册18.1 勾股定理公开课ppt课件

这是一份数学八年级下册18.1 勾股定理公开课ppt课件，共35页。PPT课件主要包含了S1+S2S3，结论仍然成立，勾股定理公式变形，本节课你有什么收获等内容，欢迎下载使用。

这是2002年在北京召开的世界数学家大会的会徽.
所作的“弦图”为原型设计的，
今天我们将要学习与这个图形相关的一个重要定理——
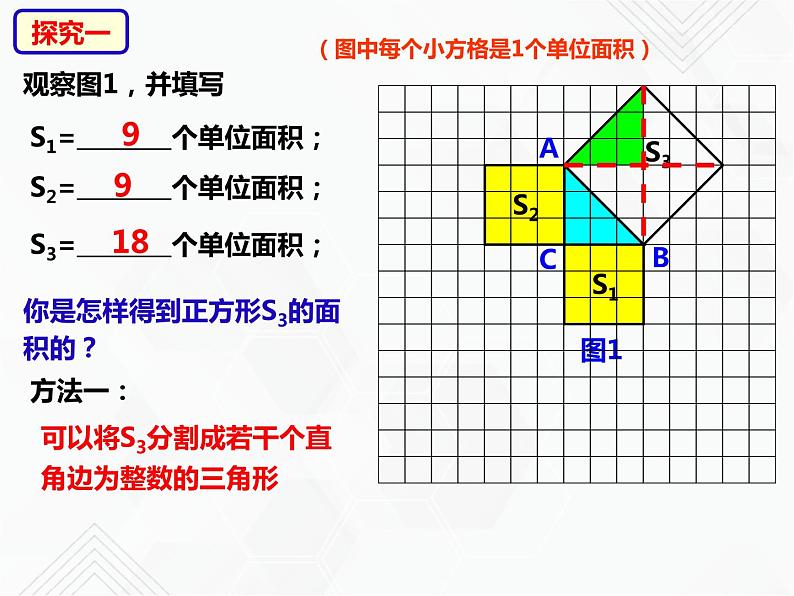
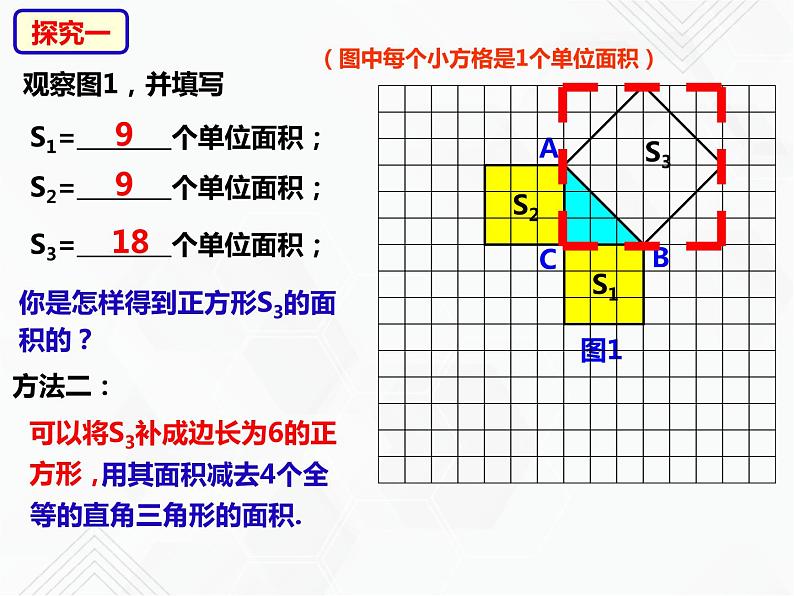
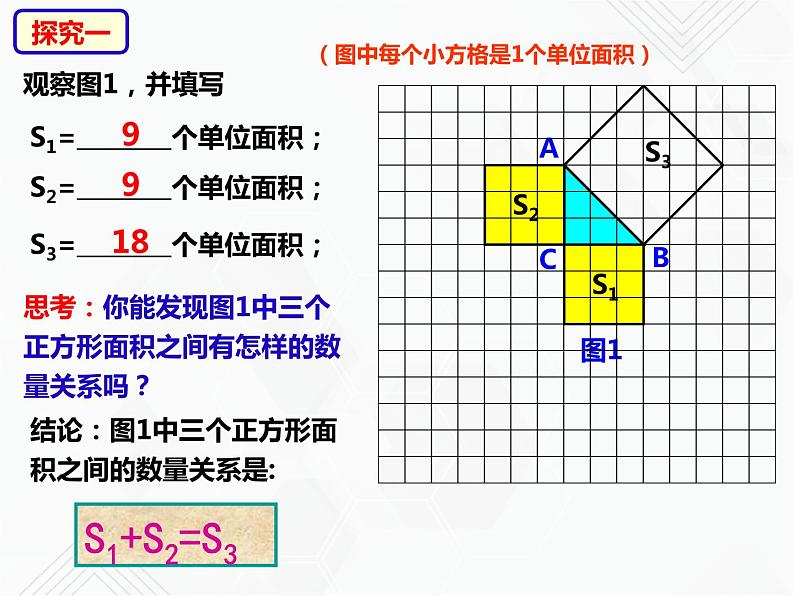
（图中每个小方格是1个单位面积）
S1= 个单位面积；
S2= 个单位面积；
S3= 个单位面积；
你是怎样得到正方形S3的面积的？
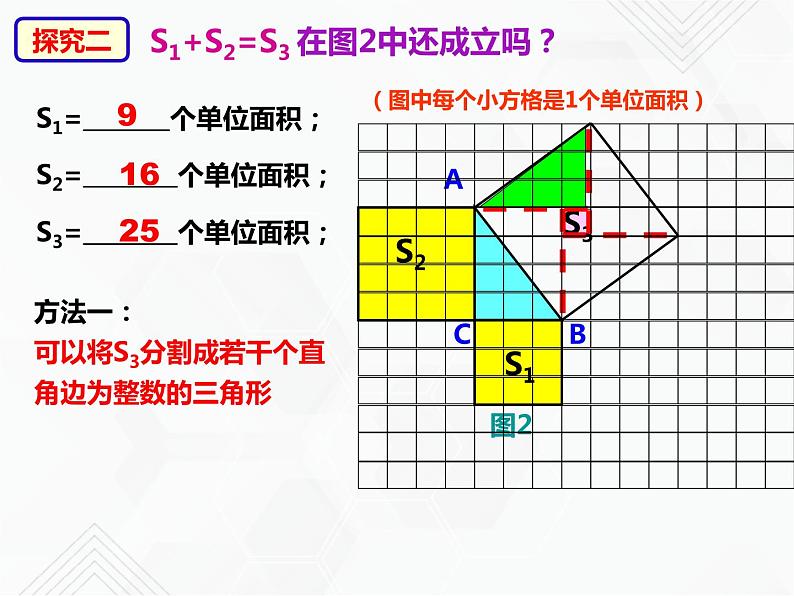
可以将S3分割成若干个直角边为整数的三角形
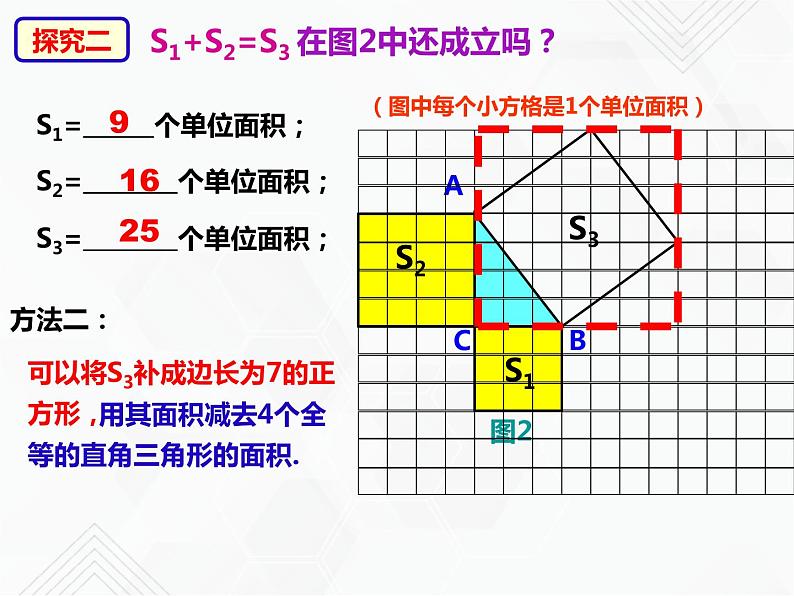
用其面积减去4个全等的直角三角形的面积.
可以将S3补成边长为6的正方形，
思考：你能发现图1中三个正方形面积之间有怎样的数量关系吗？
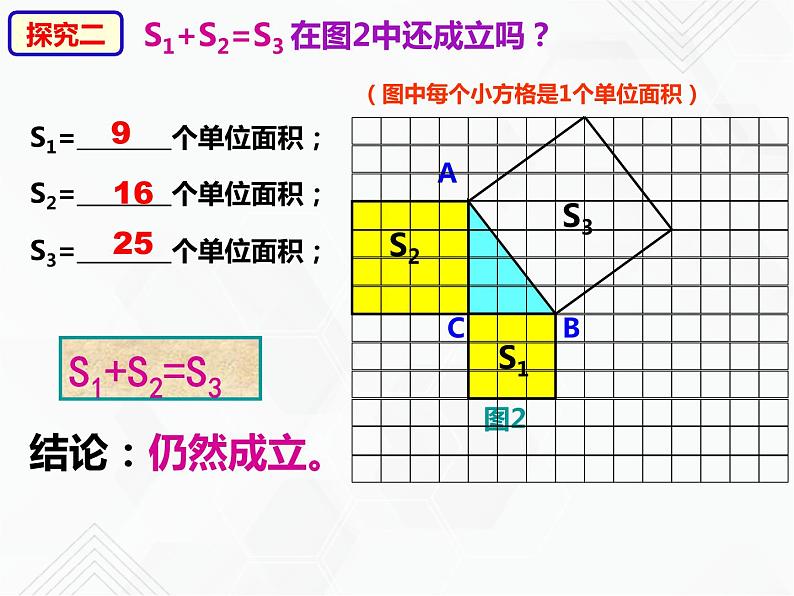
结论：图1中三个正方形面积之间的数量关系是:
S1+S2=S3 在图2中还成立吗？
S1= 个单位面积；
方法一：可以将S3分割成若干个直角边为整数的三角形
S1= 个单位面积；
可以将S3补成边长为7的正方形，
至此，我们在网格中验证了:
两条直角边上的正方形面积之和
问题2：式子S1+S2=S3能用直角三角形的三边a、b、c来表示吗?
问题4：那么直角三角形三边a、b、c之间的关系式是:
a2 + b2 = c2
问题1：去掉网格结论会改变吗？
问题3：去掉正方形结论会改变吗？
那么 a2+b2=c2.
两直角边长分别为a，b，
是不是所有的直角三角形都具有这样的结论呢？光靠实验和猜想还不能把问题彻底搞清楚。
这就需要我们对一般的直角三角形进行证明．
下面我们就一起来探究，看一看我国古代数学家们是怎样证明这个命题的．
1、拿出准备好的四个全等的直角三角形（设直角三角形的两条直角边分别为a，b，斜边c）；
2、你能用这四个直角三角形拼成一个正方形吗？拼一拼试试看
3、你拼的正方形中是否含有以斜边c为边的正方形？
4、你能否就你拼出的图说明 a2+b2=c2？
∴ c2=b2-2ab+a2+ 2ab
大正方形的面积可以表示为( )；也可以表示为( ).
该图是2002年在北京召开的世界数学家大会的会徽.被称为“赵爽弦图”.
∴ a2+2ab+b2 = 2ab +c2
大正方形的面积可以表示为 ( )；也可以表示为( ).
∴ (a+b)2 =
你能只用两个直角三角形来说明
梯形的面积可以表示为 ( )；也可以表示为( ).
a2 + b2 = c2
1881年，伽菲尔德就任美国第二十任总统.后来，人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明，就把这一证法称为“总统证法”．
在中国古代，人们把弯曲成直角的手臂的上半部分称为“勾”，下半部分称为“股”.
直角三角形中较短的直角边称为勾，
我们称上述定理为勾股定理，
国外称为毕达哥拉斯定理.
如果直角三角形的两直角边用a，b表示，斜边用c表示，那么勾股定理可表示为
∴ a2+b2=c2
∵ △ABC为直角三角形，∠C=90°
(或 BC2+AC2=AB2）
这个定理在中国又称为“商高定理”，商高是公元前十一世纪的中国人.当时中国的朝代是西周，是奴隶社会时期.在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话.商高说：“…故折矩，勾广三，股修四，经隅五.”商高那段话的意思就是说：当直角三角形的两条直角边分别为3（短边）和4（长边）时，径隅（就是弦）则为5.以后人们就简单地把这个事实说成“勾三股四弦五”.由于勾股定理的内容最早见于商高的话中，所以人们就把这个定理叫做“商高定理”.
b2= c2 - a2
a2= c2 - b2
① 勾股定理内容描述的是
直角三角形三边之间的数量关系
1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为( )
A.3 米 B.4 米 C.5米 D.6米
A、a2、(襄阳市中考) 如图，每个小正方形的边长为1，△ABC的三边a，b，c的大小关系是（ ）.
3、一个正方形的对角线为 ，则这个正方形的面积为（ ）
A、 B. 32 C、64 D.
4、在△ABC中，∠C=90°，AB=c，BC=a，AC=b.
(1) a=6，b=8，求 c；
(2) a=8，c=17，求 b；
(1) ∵ ∠C=90°，a=6，b=8
∴ c2=a2+b2
勾股定理的主要作用是 ：
(2) ∵ ∠C=90°，a=8，c=17
∴ b2=c2-a2
(3) 已知 a:b=2:1 ，c=5，求 a，b.
(3) ∵ a:b=2:1
∴ 设 a=2x，b=x
即 (2x)2+x2=52
∴ a=2x= ，
5、如图，楼梯的高度为2m，楼梯坡面的长度为4m，要在楼梯的表面铺上地毯，那么地毯的长度至少需要多少米？(精确到0.1m)
解：给三角形楼梯的三个角分别标上A、B、C，
答：地毯的长度至少需要5.5米.
则地毯的长度等于AB+BC的长度.
∵ ∠B=90°，AB=2，AC=4
6、学以致用：(1) 求图中字母所代表的正方形的面积。
斜边上的正方形面积.
S7=S5+S6 =10
7、已知直角三角形的两边长分别为3,4，求第三条边的长.
(1) 当直角边长分别为3和4时，
(2) 当斜边长为4时，
解：∵ ∠c=90°，AC=12，BC=5
8、如图，一根电线杆在离地面5米处断裂，电线杆顶部落在离电线杆底部12米处，电线杆折断之前有多高？
∴ 电线杆折断之前的高度为
9、已知：如图，在Rt△ABC中，两直角边 AC=5，BC=12.求斜边上的高 CD 的长.
解：∵ 在 Rt△ABC 中，∠ACB=90°， AC=5，BC=12
又∵ Rt△ABC的面积：
10、如图，一架梯子长25m，斜靠在一面墙上，梯子底端离墙7m.
(1) 这个梯子的顶端距地面有多高？
(2) 如果梯子的顶端下滑了4m，那么梯子的底端在水平方向上滑动了几米？
(3) 当梯子的顶端下滑的距离与梯子的底端水平滑动距离相等时，这时梯子的顶端距离地面有多高？