沪科版17.1 一元二次方程优质课课件ppt

这是一份沪科版17.1 一元二次方程优质课课件ppt，共59页。PPT课件主要包含了一元二次方程的应用等内容，欢迎下载使用。

能使一元二次方程左右两边相等的
只含有一个未知数（元），
并且未知数的最高次数是 2 的
ax2+bx+c=0
（a≠0， ）
一元二次方程的解（或根）
2、一元二次方程的一般形式是什么？
1、什么是一元二次方程？
3、什么是一元二次方程的解（或根）？
1、判断下列方程中，哪些是关于x的一元二次方程？
(2) 4x2+3x-2=(2x-1)2
(3) x3-x+4=0
(4) x2-2y-3=0
(5) (m+1)x2+3x+1=0
一元二次方程必须满足三个条件
① 只含有一个未知数（元）
2、若方程 是关于x的一元二次方程，求m的值.
∵ 是关于x的一元二次方程
∴
所以既要保证未知数的最高次数是2，
又要保证二次项系数不等于 0 .
注意： 因为所给方程是关于x的一元二次方程，
3、 已知关于x的方程 (k2-1)x2+(k+1)x-2=0.
(1) 当k为何值时是一元一次方程？
∴ 当k=1时，原方程是一元一次方程
(2) 当k为何值时是一元二次方程？
∴ 当k≠±1时，原方程是一元二次方程
4、已知关于x的一元二次方程 (m-2)x2+3x+m2-4=0 有一个根是 0，求m的值.
∵ 0是方程 (m-2)x2+3x+m2-4=0 的一个根
又∵ 方程 (m-2)x2+3x+m2-4=0 是关于x的一元二次方程
因此，求一元二次方程中的字母的值时，
只需把已知方程的根代入原方程就可以求出字母的值.
注意： 方程的根就是使方程左右两边相等的未知数的值，
5、（2018扬州中考）若 m 是方程 2x2-3x-1=0 的一个根，求 6m2-9m+2015 的值.
∵ m是方程 2x2-3x-1=0 的一个根
∴ 2m2-3m-1=0
∴ 2m2-3m=1
∴ 6m2-9m+2015
= 3（2m2-3m）+2015
6、已知实数a是一元二次方程 x2-2020x+1=0的一个根，求代数式
∵ 实数a是方程 x2-2020x+1=0 的一个根
∴ a2-2020a+1=0
∴ a2+1=2020a，
a2-2020a=-1
= a2-2019a-a
= a2-2020a
7、m是方程 x2+x-1=0 的根，求 m3+2m2+2015的值.
∵ m是方程 x2+x-1=0 的一个根
∴ m2+m-1=0
∴ m3+2m2+2015
= m3+m2+m2+2015
= m(m2+1)+m2+2015
= m+m2+2015
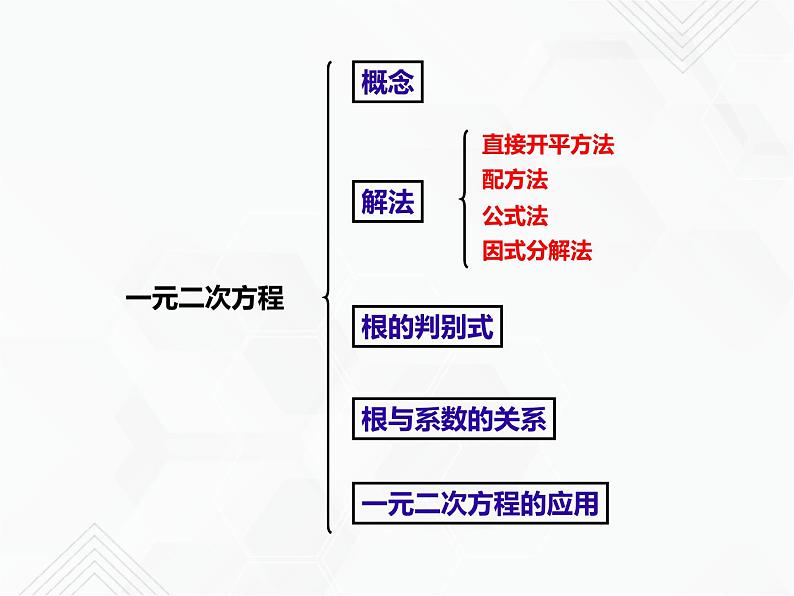
1、解一元二次方程的方法有哪些？
2、解一元二次方程的基本思想是什么？
转化为两个一元一次方程，
把一个一元二次方程“降次”，
我们把这种思想称为“降次转化思想.”
用直接开平方法解下列方程.
① 把原方程化成 或 这种形式；
用直接开平方法解一元二次方程的一般步骤.
③ 解一元一次方程，求出方程的根.
② 开平方，把一元二次方程化成一元一次方程，也就是把二次降为一次；
形如 或 的一元二次方程.
(1) 2x2-3x-1=0
当二次项系数1，且一次项系数是偶数时，用 较简单
(2) x2+2x-9999=0
x2+2x+1=9999+1
(x+1)2=10000
用 配方法 解一元二次方程的步骤:
① 把方程化为一般形式，
⑤ 写出一元二次方程的两个根.
把常数项移到方程的右边；
方程两边同时加上一次项系数绝对值
当方程右边是非负数时，
用直接开平方法解方程.
∴ b2 - 4ac=
将原方程化成标准形式，得
22 - 4×2×(-1)=
(a≠0，且b2-4ac≥0)
（b2 - 4ac ≥0）
代入求根公式求解；
用公式法解一元二次方程的一般步骤：
① 把一元二次方程化为一般形式 ax2+bx+c=0 (a≠0)
② 确定方程中 a，b，c 的值
③ 求出 b2 - 4ac 的值
④ 若 b2 - 4ac≥0 ，
若 b2 - 4ac<0 时，
则把a，b，c 及b2 - 4ac的值
5(2x-1)=(1-2x)(x+3)
用因式分解法解下列方程.
把方程左边因式分解，得
(2x-1) [5+(x+3)]＝0
5(2x-1)-(1-2x)(x+3)=0
(2x-1)(x+8)＝0
② 将方程的左边因式分解；
用因式分解法解一元二次方程的基本步骤
① 将方程变形，使方程的右边为零；
③ 根据若a·b=0，
④ 写出原方程的解.
1、四种解法中，最简便的解法的是
最后选择配方法.
在没有规定方法的前提下解一元一次方程时，
2、解一元二次方程方法的选择顺序：
当二次项系数1，且一次项系数是偶数时，用 较简单.
① x2-3x+1=0 ② 3x2-1=0 ③ -3t2+t=0 ④ x2-4x=2 ⑤ 2x2－x=0 ⑥ 5(m+2)2=8 ⑦ 3y2-y-1=0 ⑧ 2x2+4x-1=0 ⑨ (x-2)2=2(x-2) 适合运用直接开平方法 ； 适合运用因式分解法 ； 适合运用公式法 ； 适合运用配方法 .
题中某个含原未知数 x的式子，
因此，我们可以通过换元法来解.
可以发现两个分式互为倒数.
先用一个新的未知数 y
设 y= ，
方程两边同乘以 2y，整理，得
y1= ，
化简 ，得
化简 ，得
(-1)2-4×2×2
∴ 这个方程没有实数根
经检验：x1=x2=1 是原方程的根
综上所述： 这个方程的根为 x1=x2=1
2、求代数式 2x2-6x+7 的最小值.
= 2(x2-3x)+7
∴ 2x2-6x+7的最小值是
3、求代数式 4-x2+2x 的最大值.
=-（x2-2x）+4
=-（x2-2x+1-1）+4）
=-[(x-1)2-1]+4
又∵ -(x-1)2≤0
∴ -(x-1)2+5
∴ 4-x2+2x 的最大值是 5
由 b2-4ac 来确定.
一元二次方程ax2+bx+c=0（a≠0)的
即 △=b2-4ac.
一元二次方程 ax2+bx+c=0（a≠0) 的根的情况
我们把 b2-4ac
通常用符号“△”来表示，

一般地，一元二次方程ax2+bx+c＝0（a≠0），

有两个不相等的实数根；
当方程有两个实数根时，
当方程有两个相等的实数根时，
当方程有两个不相等的实数根时，
一元二次方程的根的判别式
(1) 25y2+4=20y
1、不解方程，判别下列方程根的情况：
原方程有两个相等的实数根.
把原方程化为标准形式，得
25y2-20y+4=0
利用一元二次方程根的判别式时，
一定要把方程化为标准形式.
2、[中考·凉山州] 关于x的一元二次方程 (m-2)x2+2x+1=0 有实数根，求m的取值范围？
∵ 关于x的一元二次方程 (m-2)x2+2x+1=0 有实数根
且 22-4(m-2)≥0
3、已知关于 x 的一元二次方程 x2+(4m+1)x+2m-1=0.求证：不论m为何实数，方程总有两个不相等的实数根.
不论m为何实数，方程总有两个不相等的实数根.
∵ 方程 m2x2+(2m+1)x+1=0 有实数根
1、关于x的方程 m2x2+(2m+1)x+1=0 有实数根，求m的取值范围.
此方程为一元一次方程，
此方程为一元二次方程.
∴ ∆=(2m+1)2-4m2
当 时，
关于x的方程 m2x2+(2m+1)x+1=0 有实数根
一元二次方程的根与系数之间存在什么关系.
这就是 根与系数 的关系，
如果 ax2+bx+c=0 (a≠0)
x1+x2= ，
1、利用韦达定理的前提条件是
要先把一元二次方程化为一般形式.
一元二次方程的根与系数之间的关系
∵ 方程 x2-(k+1)x+3k=0 的一个根是 2
综上所述：方程的另一个根是-3 , k的值是-2.
1、已知方程 x2-(k+1)x+3k=0 的一个根是 2 ,求它的另一个根及k的值.
22-2(k+1)+3k=0
∴ 方程的另一个根是－3
1、已知方程 x2-(k+1)x+3k=0 的一个根是 2 ,求它的另一个根及k的值.
设方程的另一个根为 x2.
综上所述：方程的另一个根是 -3 , k的值是 -2.
2、 设 a，b 是方程 x2+x-2015=0 的两个实数根，求 a2+2a+b 的值.
∵ a是方程 x2+x-2015=0 的根
∴ a2+a-2015=0
∴ a2+a=2015
又∵ a，b 是方程 x2+x-2015=0 的两个实数根
3、已知 x1，x2 是一元二次方程 4kx2-4kx+k+1=0 的两个实数根.
(1) 求k的取值范围；
(2) 是否存在实数k，使 (2x1-x2)(x1-2x2)=- 成立？若存在求出K的值；若不存在，请说明理由.
∵ x1，x2 是一元二次方程 4kx2-4kx+k+1=0 的两个实数根.
(-4k)2-4×4k×(k+1)≥0，
(1) 求K的取值范围；
一般先将所求的代数式化成含两根之和，
在计算与方程的根有关的代数式和等式时，
常用代数式变形方法总汇
=（x1+x2）2 -2x1x2
2、（x1-x2）2
=（x1+x2）2 - 4x1x2
某省为解决农村饮水问题，省财政部门共投资20亿元对各市的农村饮用水的“改水工程”予以一定比例的补助，2014年，A市在省财政补助的基础上再投入600万元用于“改水工程”，计划以后每年以相同的增长率投资，2016年该市计划投资“改水工程”1176万元.(1)求A市投资“改水工程”的年平均增长率；(2)从2014年到2016年，A市三年共投资“改水工程”多少万元？
题型一： 增长率（或降低率）问题的规律
解：(1)设A市投资“改水工程”年平均增长率为x,
600(1+x)2＝1176
(1+x)2＝1.96
x2=-2.4不符题意，
答：A市投资“改水工程”的年平均增长率为40%.
(2) 600+600×(1+0.4)+1176
答：A市三年共投资“改水工程”2616万元.
则一次增长后的值为
增长率（或降低率）问题的规律
则一次降低后的值为
题型二： 利用一元二次方程解决销售与利润问题
某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元. 为了尽快减少库存，商场决定采取降价措施. 经调查发现：如果这种衬衫的售价每降低1元，商场平均每天可多售出2件.
(1) 若商场要想平均每天盈利1200元，每件衬衫应降价多少元?
分析：设每件衬衫应降价x元，
则把题中信息整理成下表:
解：设每件衬衫应降价x元.
(40-x)(20+2x)=1200
答：商场要想平均每天盈利1200元，每件衬衫应降价20元.
∴ 每件衬衫应降价20元.
某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元. 为了尽快减少库存，商场决定采取降价措施. 经调查发现：如果这种衬衫的售价每降低1元，商场平均每天可多售出2件.
(2) 每件衬衫降价多少元时，商场每天盈利最多？最多盈利多少元？
解：设每件衬衫应降价x元，
W=(40-x)(20+2x)
=-2x2+60x+800
=-2（x-15）2+1250
答：每件衬衫降价15元时，商场每天盈利最多,最多盈利1250元.
1、如图,在一块长92m,宽60m的矩形耕地上挖三条水渠,水渠的宽度都相等.水渠把耕地分成面积均为885m2的6个矩形小块,水渠应挖多宽.
题型三： 利用一元二次方程解决图形面积（体积）问题
(92-2x)(60-x)=885
x2-106x＋105=0
x2＝105不符题意，
2、[中考·襄阳]如图，一农户要建一个长方形猪舍，猪舍的一边利用长为12m的住房墙，另外三边用25m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1m宽的门.所围长方形的长、宽分别为多少时，猪舍的面积为80m2？
解：设长方形的宽为 x m，
则长为（26-2x) m.
x(26-2x)=80
答：所围长方形的长为10m，宽为8m时，猪舍的面积为80m2
3、如图所示，在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如果要使整个挂图的面积是5400cm2，求金色纸边的宽.
解：设金色纸边的宽为xcm.
(80+2x)(50+2x)=5400
x2＝-70 不符题意，
答：如果要使整个挂图的面积是5400cm2，则金色纸边的宽为5cm.
1、春节时有一些同学相约每两人互通一次电话，他们一共打了45次电话.请问有多少名同学相约互相通电话？
答：有10名同学相约互相通电话.
题型四： 利用一元二次方程解决传播问题
解：设有x名同学相约互相通电话.根据题意，得
2、 有一人患了流感，经过两轮传染后共有64人患了流感.（1）求每轮传染中平均一个人传染了几个人？（2）如果不及时控制，第三轮将又有多少人被感染？
答：每轮传染中平均一个人传染了7人，如果不及时控制，第三轮将又有448人被感染.
题型四 ： 利用一元二次方程解决传播问题
解：(1)设每轮传播中平均一个人传染了x人.
1+x+x(1+x) = 64
(2) 64×7=448(人)
则中巴车每小时行驶(x+20)千米.
变式练习： 在高速公路上，A，B两地间的距离为300千米，中巴车每小时比大客车多行20千米，因而行驶全程少用45分钟，求两车的速度.
分析：设大客车每小时行驶x千米，
变式练习：在高速公路上，A，B两地间的距离为300千米，中巴车每小时比大客车多行20千米，因而行驶全程少用45分钟，求两车的速度.
则中巴车每小时行驶(x+20)千米.
解：设大客车每小时行驶x千米，
方程两边同乘以 4x(x+20)，整理，得
x2+20x-8000=0
x1=80 ，x2=-100
1、已知关于x的一元二次方程 x2-(2k+1)x+4( k- )=0.
无论k取何值，方程总有实数根
4×4(k- )
(1) 求证：无论k取何值，方程总有实数根；
(2) 若等腰三角形ABC的一边长为a=4，另两边b、c恰好是这个方程的两个根，求△ABC的周长.
2、已知：关于x的方程kx2－(3k－1)x＋2(k－1)＝0. (1)求证：无论k为何实数，方程总有实数根； (2)若此方程有两个实数根x1，x2，且|x1－x2|＝2，求k的值．
∴ 无论k为何实数，方程总有实数根
∵ Δ＝b2-4ac=
[-(3k－1)]2-4k·2(k-1)
3、已知关于x的方程 x2-(m＋2)x＋(2m-1)＝0. (1)求证：方程恒有两个不相等的实数根； (2)若此方程的一个根是1，请求出方程的另一个根，并求出以此两根为边长的直角三角形的周长．