八年级上册2 平面直角坐标系多媒体教学课件ppt

这是一份八年级上册2 平面直角坐标系多媒体教学课件ppt，共17页。PPT课件主要包含了情景导入，平面直角坐标系，教材解析，解A-20，B0-3，C3-3，D40，E33，F03，典例透析等内容，欢迎下载使用。

第三章 位置与坐标2 平面直角坐标系
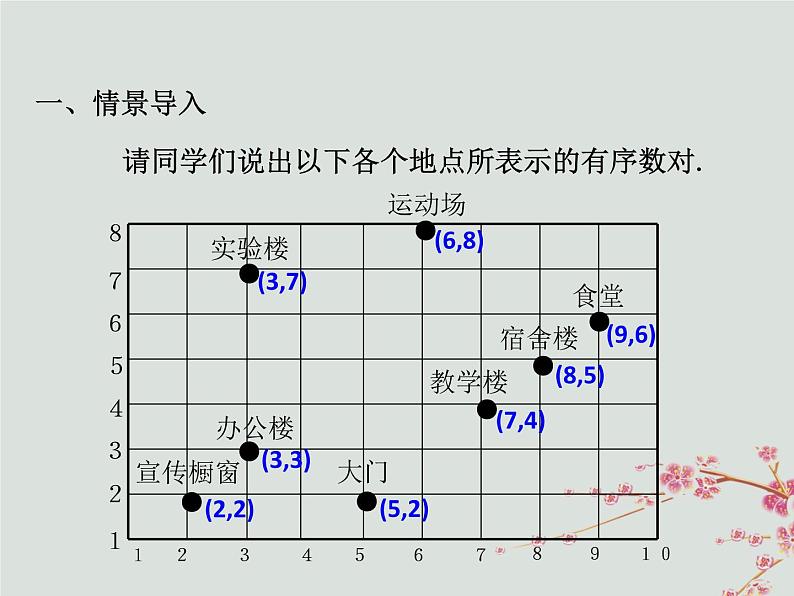
请同学们说出以下各个地点所表示的有序数对.
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

A点是（０，０）B点是（２，１）
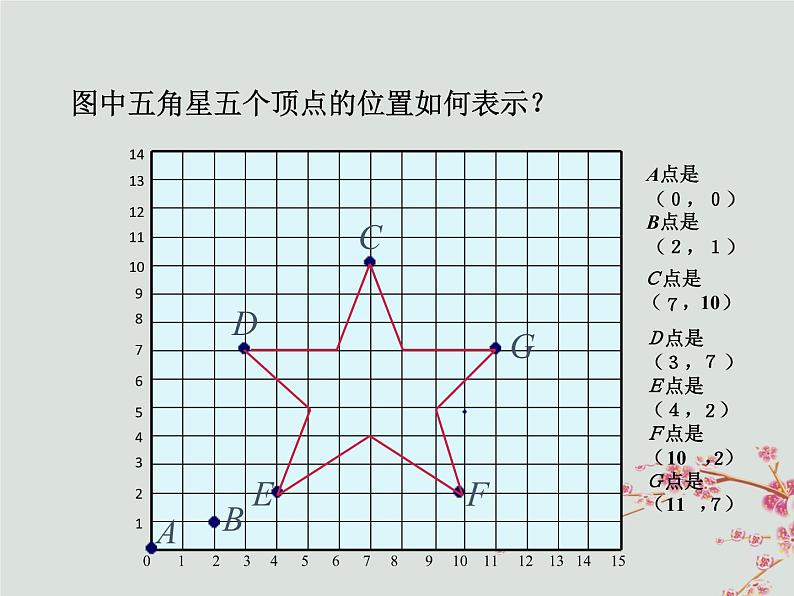
　图中五角星五个顶点的位置如何表示？
Ｄ点是（　，　）Ｅ点是（　， ）Ｆ点是（　　，）Ｇ点是（　 ， ）
1.知识目标（1）通过复习使学生掌握平面直角坐标系的相关概念；（2）掌握坐标系中特殊位置点的坐标规律.2.教学重点 相关知识的回顾，各种不同情境中点的坐标求法.3.教学难点 较复杂背景中点的坐标求法.
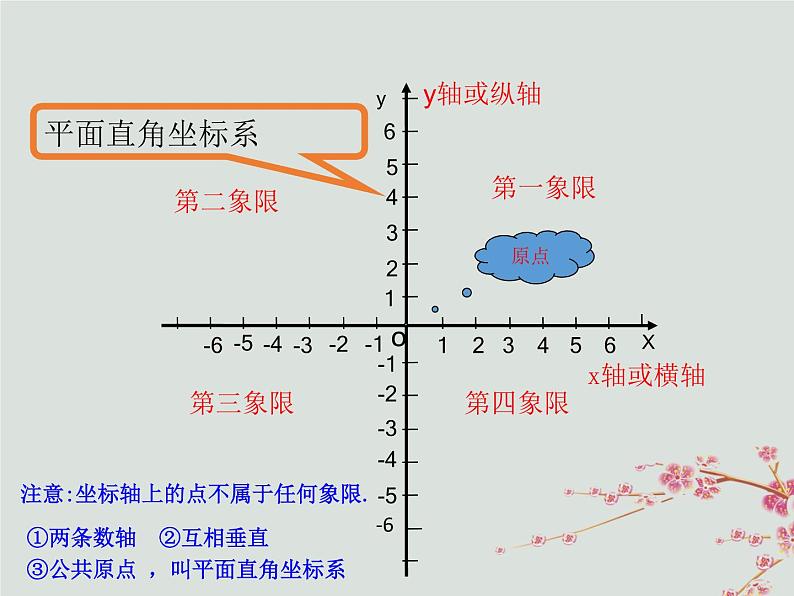
特点：①两条数轴互相垂直 ②公共原点
在平面内，两条互相垂直且有公共原点的数轴组成平面直角坐标系.
-4 -3 -2 -1
①两条数轴　②互相垂直　③公共原点 ，叫平面直角坐标系
注意:坐标轴上的点不属于任何象限.
----------------------
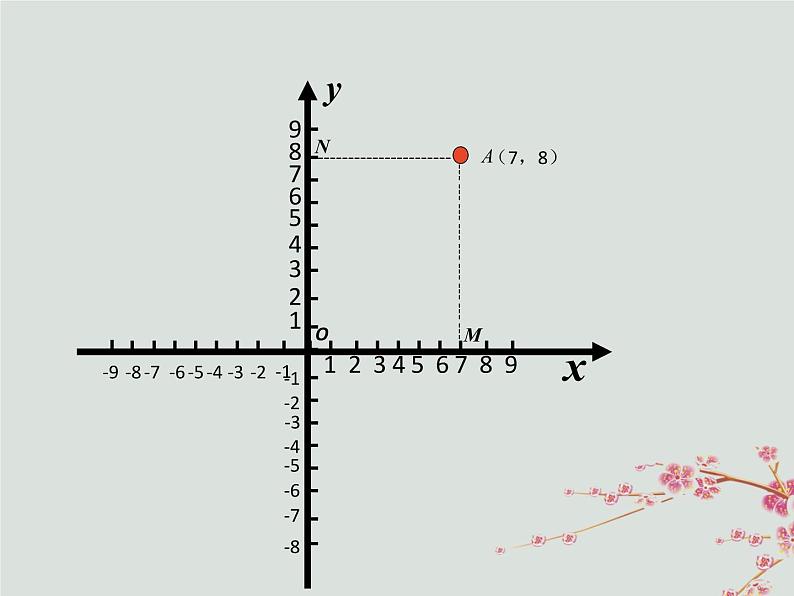
A点的坐标记作A(7，8).
(1).过A点向x轴作垂线，垂足M在x轴上的坐标是7,A点的横坐标为7；
(2).过A点向y轴作垂线,垂足N 在y 轴上的坐标是8,A点的纵坐标为8.
2.如何确定平面直角坐标系中点的坐标？
我们规定：横坐标在前,纵坐标在后
例1 在坐标系中标出下列各点的坐标，并依次连接各点.
1.点B与C的纵坐标相同，线段BC的位置有什么特点？纵坐标相同的点的连线平行于x轴2.线段CE的位置有什么特点？横坐标相同的点的连线平行于y轴3.坐标轴上的点的坐标有什么特点？ x轴上的点的纵坐标为0，表示为（x，0） y轴上的点的横坐标为0，表示为（0，y）
例2 如图, 矩形ABCD的长宽分别是6 , 4 , 建立适当的坐标系,并写出各个顶点的坐标.
解: 如图,以点C为坐标原点, 分别以CD , CB所在的直线为x 轴,y 轴建立直角坐标系. 此时C点坐标为( 0 , 0 ).
由CD长为6, CB长为4, 可得D , B , A的坐标分别为D( 6 , 0 ), B( 0 , 4 ),A( 6 , 4 ) .
　例3　一个直四棱柱的俯视图如图所示.请建立适当的坐标系，在直角坐标系中作出俯视图，并标出各顶点的坐标.
解　建立直角坐标系如图，选择比例为1：10.取点E为直角坐标系的原点，使俯视图中的线段AB在x 轴上，
则可得A，B，C，D各点的坐标分别为（-1，0），（2，0），（2.5，1.5），（0，3.5）.
根据上述坐标在直角坐标系中作点A、B、C、D，并用线段依次连结各点.如图就是所求作的俯视图.
1.点（-1，2）在（ ）
A.第一象限 B.第二象限 C.第三象限 D. 第四象限
2.若点（x，y）在第四象限内，则（ ）
A. x ， y同是正数 B. x ， y同是负数 C. x是正数， y是负数 D. x是负数， y是正数
3.横坐标是正数，纵坐标的绝对值是正数的点在（ ）
A.第一、三象限 B.第二、四象限 C.第二、三象限 D.第一、四象限
4.若点P（a，b）在第二象限，则点Q（-a，b+1）在（ ） A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.点 M（- 8，12）到 x轴的距离是 ， 到 y轴的距离是 .
6.若点P在第三象限且到x轴的距离为4，到y轴的距离为 1.5，则点P的坐标是 .
4.x轴上的点P到y轴的距离为2.5,则点Ｐ的坐标为（ 　） Ａ.（2.5,0) 　 B . (-2.5,0) 　 C .(0,2.5) D . (2.5,0)或(-2.5,0)
7. 如图正三角形ABC的边长为 6 , 建立适当的直角坐标系 ,并写出各个顶点的坐标 .
解: 如图,以边AB所在的直线为x 轴,以边AB的中垂线y 轴建立直角坐标系.