数学必修 第二册第13章 立体几何初步13.1 基本立体图形优秀课后测评

这是一份数学必修 第二册第13章 立体几何初步13.1 基本立体图形优秀课后测评，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

(建议用时：40分钟)





一、选择题


1．下列说法正确的是( )


A．平行于圆锥某一母线的截面是等腰三角形


B．平行于圆台某一母线的截面是等腰梯形


C．过圆锥顶点与底面圆心的截面是等腰三角形


D．过圆台上底面中心的截面是等腰梯形


C [由圆柱、圆锥、圆台的性质知C正确．]


2．正方形绕其一条对角线所在直线旋转一周，所得空间图形是( )


A．圆锥 B．圆台


C．圆柱 D．两个圆锥组合体


D [连接正方形的两条对角线知对角线互相垂直，故绕其一条对角线旋转一周形成两个圆锥的组合体．]


3．一个正方体内接于一个球，过球心作一截面，则截面不可能的图形是( )





A B C D


D [当截面平行于正方体的一个侧面时得C，当截面过正方体的体对角线时得B，当截面不平行于任何侧面也不过对角线时得A，但无论如何都不能截出D．]


4．线段y＝2x(0≤x≤2)绕x轴旋转一周所得的图形是( )


A．圆台B．圆锥


C．圆锥侧面 D．圆台侧面


C [由线段y＝2x(0≤x≤2)绕x轴旋转一周，得到的是圆锥侧面，不含底面．]


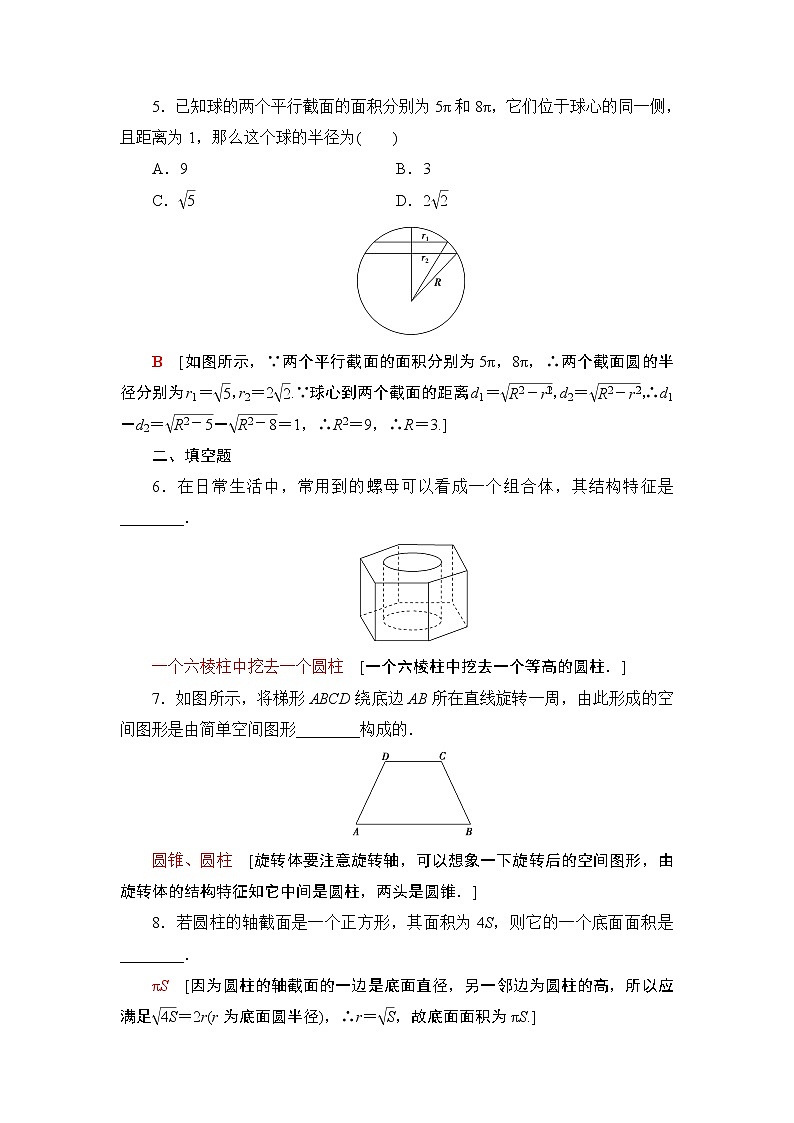
5．已知球的两个平行截面的面积分别为5π和8π，它们位于球心的同一侧，且距离为1，那么这个球的半径为( )


A．9 B．3


C．eq \r(5) D．2eq \r(2)





B [如图所示，∵两个平行截面的面积分别为5π，8π，∴两个截面圆的半径分别为r1＝eq \r(5)，r2＝2eq \r(2).∵球心到两个截面的距离d1＝eq \r(R2－r\\al(2,1))，d2＝eq \r(R2－r\\al(2,2))，∴d1－d2＝eq \r(R2－5)－eq \r(R2－8)＝1，∴R2＝9，∴R＝3.]


二、填空题


6．在日常生活中，常用到的螺母可以看成一个组合体，其结构特征是________．





一个六棱柱中挖去一个圆柱 [一个六棱柱中挖去一个等高的圆柱．]


7．如图所示，将梯形ABCD绕底边AB所在直线旋转一周，由此形成的空间图形是由简单空间图形________构成的．





圆锥、圆柱 [旋转体要注意旋转轴，可以想象一下旋转后的空间图形，由旋转体的结构特征知它中间是圆柱，两头是圆锥．]


8．若圆柱的轴截面是一个正方形，其面积为4S，则它的一个底面面积是________．


πS [因为圆柱的轴截面的一边是底面直径，另一邻边为圆柱的高，所以应满足eq \r(4S)＝2r(r为底面圆半径)，∴r＝eq \r(S)，故底面面积为πS.]


三、解答题


9．轴截面为正方形的圆柱叫作等边圆柱．已知某等边圆柱的轴截面面积为16 cm2，求其底面周长和高．


[解] 如图所示，作出等边圆柱的轴截面ABCD，由题意知，四边形ABCD为正方形，设圆柱的底面半径为r，则AB＝AD＝2r.





其面积S＝AB×AD＝2r×2r＝4r2＝16 cm2，解得r＝2 cm.


所以其底面周长C＝2πr＝2π×2＝4π(cm)，高h＝2r＝4 cm.


10．从一个底面半径和高都是R的圆柱中挖去一个以圆柱上底面为底，下底面中心为顶点的圆锥，得到如图所示的空间图形，如果用一个与圆柱下底面距离等于l并且平行于底面的平面去截它，求所得截面的面积．





[解] 轴截面如图所示，被平行于下底面的平面所截的圆柱的截面圆的半径O1C＝R，设圆锥的截面圆的半径O1D为x.因为OA＝AB＝R，所以△OAB是等腰直角三角形．又CD∥OA，则CD＝BC，所以x＝l，故截面面积S＝πR2－πl2＝π(R2－l2)．








1．(多选题)以下说法不正确的是( )


A．圆台上底面的面积与下底面的面积之比一定小于1


B．矩形绕任意一条直线旋转都可以围成圆柱


C．直角三角形绕其一边所在直线旋转一周都可以围成圆锥


D．圆台的上、下底面不一定平行，但过圆台侧面上每一点的母线都相等


BCD [A正确，圆台是由圆锥截得的，截面是上底面，其面积小于下底面的面积；B错误，矩形绕其对角线所在直线旋转，不能围成圆柱；C错误，绕直角边所在直线旋转可以围成圆锥，但绕斜边所在直线旋转围成的是由两个圆锥组成的组合体；D错误，圆台的上、下底面一定平行．故选BCD．]


2．以钝角三角形的较小边所在的直线为轴，其他两边旋转一周所得到的空间图形是( )





A．圆锥


B．两个圆锥组合体


C．圆台


D．一个大圆锥挖去一个同底的小圆锥


D [如图，以AB为轴旋转所得的空间图形是一个大圆锥挖去一个同底的小圆锥．]


3．我国古代数学名著《数学九章》中有云：“今有木长三丈五尺，围之4尺．葛生其下，缠木三周，上与木齐，问葛长几何？”其意思为：圆木长3丈5尺，圆周为4尺，葛藤从圆木的底部开始向上生长，绕圆木三周，刚好顶部与圆木平齐，问葛藤最少长________尺．(注：1丈等于10尺)


37 [由题意，圆柱的侧面展开图是矩形，如图所示：





一条直角边(即圆木的高)长3×10＋5＝35尺，另一条直角边长3×4＝12尺，


因此葛藤最少长为eq \r(352＋122)＝37尺．]


4．在半径为13的球面上有A，B，C三点，其中AC＝6，BC＝8，AB＝10，则球心到经过这三个点的截面的距离为________．


12 [由线段的长度知△ABC是以AB为斜边的直角三角形，所以其外接圆的半径r＝eq \f(AB,2)＝5，所以d＝eq \r(R2－r2)＝12.]


5．如图所示，已知圆锥SO中，底面半径r＝1，母线长l＝4，M为母线SA上的一个点，且SM＝x，从点M拉一根绳子，围绕圆锥侧面转到点A．求：





(1)绳子的最短长度的平方f(x)；


(2)绳子最短时，顶点到绳子的最短距离；


(3)f(x)的最大值．


[解] 将圆锥的侧面沿SA展开在平面上，如图所示，则该图为扇形，且弧AA′的长度L就是圆O的周长，





∴L＝2πr＝2π.


∴∠ASM＝eq \f(L,2πl)×360°＝eq \f(2π,2π×4)×360°＝90°.


(1)由题意知绳子长度的最小值为展开图中的AM，其值为AM＝eq \r(x2＋16)(0≤x≤4)．


f(x)＝AM2＝x2＋16(0≤x≤4)．


(2)绳子最短时，在展开图中作SR⊥AM，垂足为R，则SR的长度为顶点S到绳子的最短距离，在△SAM中，


∵S△SAM＝eq \f(1,2)SA·SM＝eq \f(1,2)AM·SR，


∴SR＝eq \f(SA·SM,AM)＝eq \f(4x,\r(x2＋16))(0≤x≤4)，


即绳子最短时，顶点到绳子的最短距离为eq \f(4x,\r(x2＋16))(0≤x≤4)．


(3)∵f(x)＝x2＋16(0≤x≤4)是增函数，


∴f(x)的最大值为f(4)＝32.