






直角三角形的性质与判定(Ⅱ)PPT课件免费下载
展开第3课时 勾股定理的逆定理
第3课时 勾股定理的逆定理
一、【学习目标】
1.通过勾股定理的逆向思考、验证、归纳,掌握直角三角形的判定方法.2.在弄清勾股定理及其逆定理的区别与联系的前提下,综合运用两个定理解决数学问题.
二、【课程的主要内容】
目标一 会用勾股定理的逆定理判定直角三角形
例1 教材例3 针对训练 已知△ABC的三边长a,b,c满足下列条件,且∠A,∠B,∠C所对的边分别为a,b,c,试判断△ABC的形状.(1)a=25,b=20,c=15;(2)a=p2-q2,b=p2+q2,c=2pq(p>q>0).
[解析] 分别计算三角形三边的平方,然后判断它们之间的关系, 根据勾股定理的逆定理判断它们是否能构成直角三角形.
解:(1)∵a2=252=625,b2=202=400,c2=152=225,∴b2+c2=a2,∴△ABC是直角三角形,且∠A=90°.(2)∵a2=(p2-q2)2=p4-2p2q2+q4,b2=(p2+q2)2=p4+2p2q2+q4,c2=(2pq)2=4p2q2,∴a2+c2=b2,∴△ABC是直角三角形,且∠B=90°.
【归纳总结】由三边判定直角三角形的步骤(1)找出最长边;(2)看两条较短边的平方和是否等于最长边的平方.若相等,则是直角三角形,否则不是直角三角形.
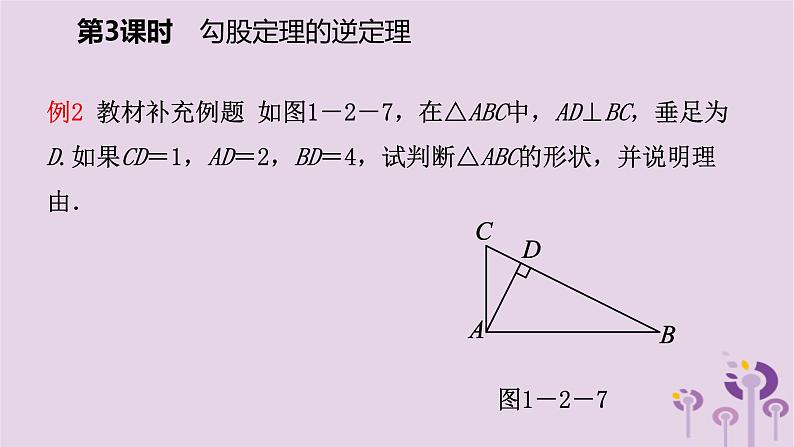
例2 教材补充例题 如图1-2-7,在△ABC中,AD⊥BC,垂足为D.如果CD=1,AD=2,BD=4,试判断△ABC的形状,并说明理由.
三、【拓展学习】
目标二 能综合应用勾股定理及其逆定理解决问题
例3 教材例4针对训练 如图1-2-8,已知在四边形ABCD中,AB=1,BC=2,CD=2,AD=3,且AB⊥BC,求四边形ABCD的面积.
[解析] 要求四边形ABCD的面积,可将它转化为两个三角形的面积之和,因为AB⊥BC,所以连接AC,可得△ABC为直角三角形,同时,根据勾股定理的逆定理可证明△ACD也是直角三角形,故四边形ABCD的面积等于Rt△ABC和Rt△ACD的面积之和.
【归纳总结】勾股定理及其逆定理综合运用的方法(1)先由勾股定理求出一个三角形的某一边长,再由勾股定理的逆定理确定另外一个三角形的形状,进而解决其他问题.(2)求不规则图形的面积常用的方法是割补法——即把不规则图形分割或拼补成规则图形,然后再用相关知识将问题解决.
知识点一 直角三角形的判定定理(勾股定理的逆定理)
定理:如果三角形的三条边长a,b,c满足关系:__________,那么这个三角形是直角三角形,______是斜边长.
满足______________的三个正整数称为勾股数.
数轴PPT课件免费下载: 人教版初中数学七年级上册课文《数轴》,完整版PPT课件免费下载,优秀PPT背景图搭配,精美的免费ppt模板。轻松备课,欢迎免费下载使用。
乘方PPT课件免费下载: 人教版初中数学七年级上册课文《乘方》,完整版PPT课件免费下载,优秀PPT背景图搭配,精美的免费ppt模板。轻松备课,欢迎免费下载使用。
角PPT课件免费下载: 人教版初中数学七年级上册课文《角》,完整版PPT课件免费下载,优秀PPT背景图搭配,精美的免费ppt模板。轻松备课,欢迎免费下载使用。













