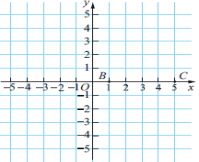苏科版八年级上册第五章 平面直角坐标系5.2 平面直角坐标系优秀教案设计
展开![]() 5.2平面直角坐标系(2)
5.2平面直角坐标系(2)
教学目标
【知识与能力】
在同一直角坐标系中,探索图形位置的变化与点的坐标变化的关系。
【过程与方法】
会用直角坐标系解决问题
【情感态度价值观】
发展形象思维能力和数形结合的意识
教学重难点
【教学重点】
点的坐标的数值变化与点的位置变化的关系的认识[
【教学难点】
探索图形位置的变化与点的坐标变化的关系
课前准备
无
教学过程
教学过程(教师) |
展示:已知点A(-1,0)、B(-5,0)、C(-3,5). (1)在下面的直角坐标系中画出这三点. (2)画出△ABC及BC边上的高AD. (3)△ABC是等腰三角形吗?AD的长是多少?
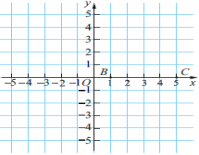
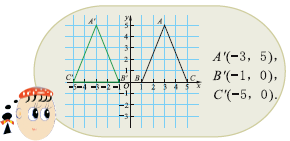
解决问题: 例3 如图,点B、点C在x轴上,试在第一象限内画点A,使△ABC为等腰三角形,BC为底,面积为10,并写出△ABC各顶点的坐标. 讨论:把△ABC沿y轴翻折得到△A′B′C′,你能写出△A′B′C′各顶点的坐标吗?
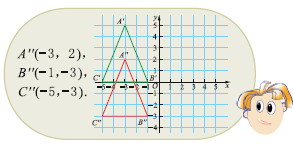
再讨论:再把△A′B′C′向下平移3个单位长度得到△A′′B′′C′′,你能写出 △A′′B′′C′′各顶点的坐标吗?
数学实验室: 探索对称点的坐标关系,强化学生对“点的坐标的数值变化与点的位置变化的关系”的认识. 1.数学实验一. (1)设计趣味性操作活动,让学生能够熟练地按所给坐标准确描出各点; (2)根据所得到的具有对称性的图案,由观察分别得到关于x轴、y轴和关于原点对称的点之间的坐标关系; (3)让学生自主观察几对关于x轴、y轴和关于原点对称的点之间坐标的关系; (4)将由观察得到的结论推广到一般情况,形成关于对称点坐标之间关系的一般认识. |
填空: (1)点(1,-3)关于x轴对称的点的坐标为______,关于y轴对称的点的坐标为_________,关于原点对称的点的坐标为 _________. (2)点(-1,3)关于x轴对称的点的坐标为________,关于y轴对称的点的坐标为______,关于原点对称的点的坐标为____________. (3)点P(a,b),关于x轴对称的点的坐标为 ________,关于y轴对称的点的坐标为_________,关于原点对称的点的坐标为_____.
2.数学实验二. (1)按要求平移线段AB到A′B′,写出平移前、后的线段端点的坐标:A(—4,1),B(—2,3), A′(3,3),B′(5,5); (2)探讨平移前、后线段端点A与A′、B与B′的横坐标之间的关系; (3)探讨平移前、后线段端点A与A′、B与B′的纵坐标之间的关系; (4)写出平移前、后线段中点D与D′的坐标,并分别探讨它们的纵坐标、横坐标之间的关系; (5)写出线段AB上任意一点C(m,n),当AB平移到A′B′后,点C′的坐标,形成关于点的坐标变化与点的位置变化关系的一般认识.
点的横坐标变化,纵坐标不变,点的位置发生了什么变化?点的纵坐标变化,横坐标不变呢? |
课堂练习: 1.填空. (1)平行于x轴的直线上不同的两个点的____坐标相同,_____坐标不同;平行于y轴的直线上不同的两个点的_____坐标相同,_____坐标不同. (2)点P(a,b), 关于x轴对称的点的坐标为( , ), 关于y轴对称的点的坐标为( , ), 关于原点对称的点的坐标为( , ). (3)图形变换后点的坐标特征: 图形左右平移,对应点的_____坐标变化,____坐标不变;图形上下平移,对应点的___ _坐标变化,_____坐标不变. 2.已知点A(a,b),B(a,c),且a≠0,b≠c,那么直线AB与坐标轴有什么位置关系? 3.已知点C(b,d),D(c,d),且d≠0,b≠c,那么直线CD与坐标轴有什么位置关系? 4.课本125页练习. |
总结: 通过这节课你学到了什么? |
数学八年级上册第五章 平面直角坐标系5.2 平面直角坐标系精品教学设计及反思: 这是一份数学八年级上册第五章 平面直角坐标系5.2 平面直角坐标系精品教学设计及反思,共4页。教案主要包含了知识与能力,过程与方法,情感态度价值观,教学重点,教学难点等内容,欢迎下载使用。
数学八年级上册5.2 平面直角坐标系优质课教案: 这是一份数学八年级上册5.2 平面直角坐标系优质课教案,共2页。教案主要包含了知识与能力,过程与方法,情感态度价值观,教学重点,教学难点等内容,欢迎下载使用。
初中数学苏科版八年级上册5.2 平面直角坐标系教案: 这是一份初中数学苏科版八年级上册5.2 平面直角坐标系教案,共2页。教案主要包含了教学目标,教学重点,教学难点,教学方法,教学过程等内容,欢迎下载使用。