数学八年级上册第三章 勾股定理3.3 勾股定理的简单应用公开课ppt课件

这是一份数学八年级上册第三章 勾股定理3.3 勾股定理的简单应用公开课ppt课件，共13页。PPT课件主要包含了问题的提出，做一做，试一试，x24等内容，欢迎下载使用。

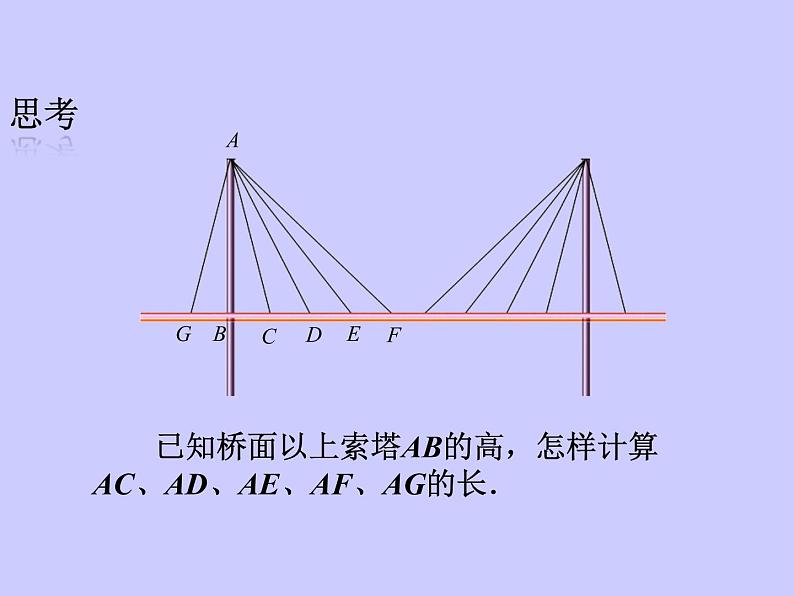
　　从远处看，斜拉桥的索塔、桥面与拉索组成许多直角三角形．
　　已知桥面以上索塔AB的高，怎样计算AC、AD、AE、AF、AG的长．
如图，有一个圆柱体，它的高等于12厘米，底面半径等于3厘米，在圆柱下底面的A点有一只蚂蚁，它想吃到上底面与A点相对的B处的食物，需要爬行的最短路程是多少？（π的值取3）
如图，一只蚂蚁从实心长方体的顶点A出发，沿长方体的表面爬到对角顶点C1处（三条棱长如图所示），问怎样走路线最短？最短路线长为多少？
分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③)，由勾股定理可求得图1中AC1爬行的路线最短.最短路线为5.
实验操作：1、（试验） 利用事先做好的圆柱体，尝试从A点到B点沿圆柱侧面画几条路线，你觉得哪条路线最短呢？
3、（计算） 蚂蚁从A点出发，想吃到B点上的食物，需要爬行的最短路程是多少？
2、（验证） 将圆柱侧面剪开展成一个长方形，从A点到B点的最短路线是什么？你画对了吗？
李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB，但他随身只带了卷尺，（1）你能替他想办法完成任务吗？
（2）李叔叔量得AD长是30厘米，AB长是40厘米，BD长是50厘米，AD边垂直于AB边吗？为什么？
（3）小明随身只有一个长度为20厘米的刻度尺，他能有办法检验AD边是否垂直于AB边吗？BC边与AB边呢？
在我国古代数学著作《九章算术》中记载了一道有趣的问题，这个问题的意思是：有一个水池，水面是一个边长为10尺的正方形，在水池的中央有一根新生的芦苇，它高出水面1尺，如果把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面，请问这个水池的深度和这根芦苇的长度各是多少？
解：设水池的水深AC为x尺，则这根芦苇长AD=AB=（x+1）尺，
在直角三角形ABC中，BC=5尺
由勾股定理得，BC2+AC2=AB2
即 52+ x2= (x+1)2
25+ x2= x2+2 x+1，
∴ x=12， x+1=13
答：水池的水深12尺，这根芦苇长13尺.
某初一（1）班的学生想知道学校旗杆的高度，他们发现旗杆上的绳子垂到地面还多1米，如图（1），当他们把绳子的下端拉开5米后，发现下端刚好接触地面，如图（2），你能帮他们把旗杆的高度和绳子的长度计算出来吗？请你与同伴交流并回答用的是什么方法.
某中学初一学生参加军训活动，某日早晨8:00全体集合整装出发，他们以6千米/时的速度向东行走.李小明由于记错了时间，9:00到校后立即骑车以12千米/时的速度向北追赶队伍，上午11:00同学们到达目的地，李小明才发觉方向错了.问:(1)李小明现在要怎样走才能离同学们最近.请你与同伴交流，并画出示意图，说明理由.(2)若李小明“打的”以60千米/时的速度去追赶同学们，沿着你画的示意图，需要多长时间赶到目的地？