苏科版八年级上册第三章 勾股定理3.3 勾股定理的简单应用完美版课件ppt

这是一份苏科版八年级上册第三章 勾股定理3.3 勾股定理的简单应用完美版课件ppt，共17页。

把勾股定理送到外星球，与外星人进行数学交流 ！ ——华罗庚
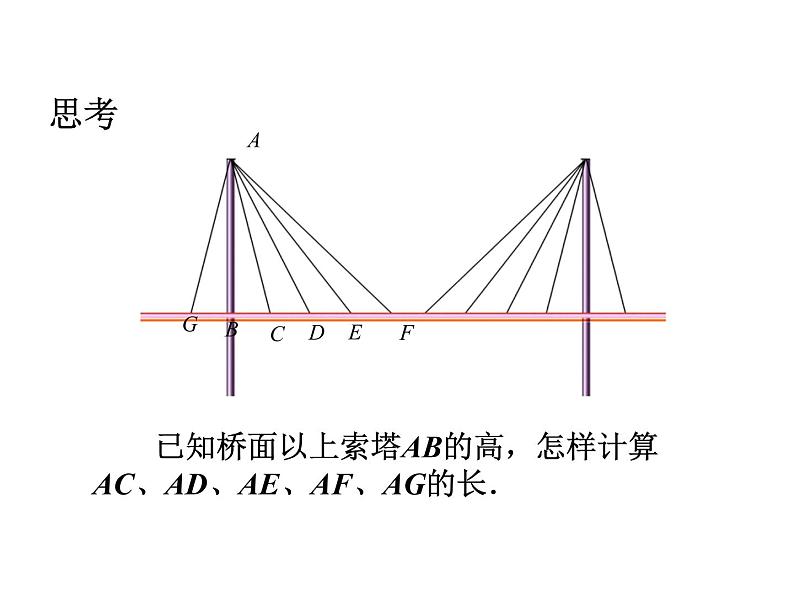
　　从远处看，斜拉桥的索塔、桥面与拉索组成许多直角三角形．
　　已知桥面以上索塔AB的高，怎样计算AC、AD、AE、AF、AG的长．
例1　九章算术中的“折竹”问题：今有竹高一丈，末折抵地，去根三尺，问折者高几何？
解：如图，我们用线段OA和线段AB来表示竹子，其中线段AB表示竹子折断部分，用线段OB来表示竹梢触地处离竹根的距离．设OA＝x，则AB＝10－x．
∵∠AOB＝90°，∴OA2＋OB2＝AB2，∴x2＋32＝（10－x）2．OA=X=91/20
利用勾股定理中哪个知识解题？
例2　如图，在△ABC中， AB＝26，BC＝20，BC边上的 中线AD＝24，求AC.
∴BD＝CD＝ BC＝ ×20＝10．∵AD2＋BD2＝576＋100＝676， AB 2＝262＝676，
勾股定理逆定理判断直角三角形
1.一个三角形的三边长的比为3:4:5，它的周长是60cm.求这个三角形的面积.
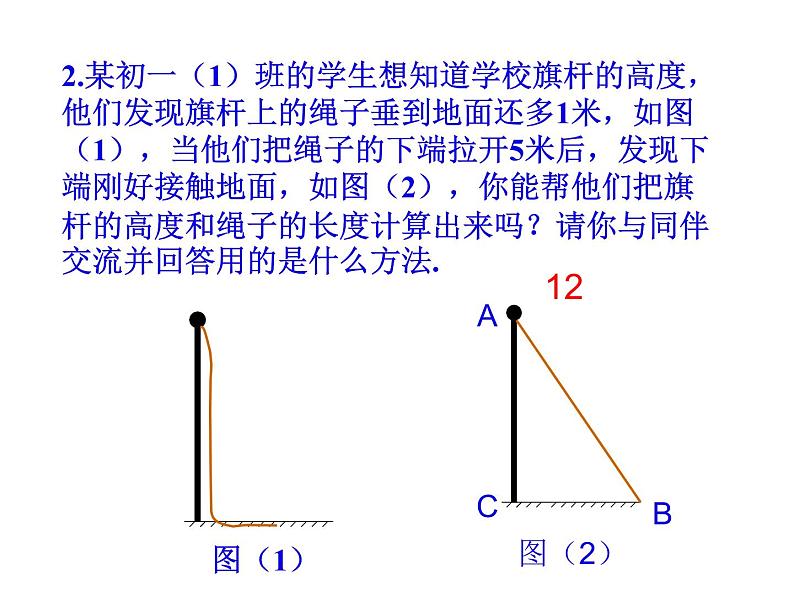
2.某初一（1）班的学生想知道学校旗杆的高度，他们发现旗杆上的绳子垂到地面还多1米，如图（1），当他们把绳子的下端拉开5米后，发现下端刚好接触地面，如图（2），你能帮他们把旗杆的高度和绳子的长度计算出来吗？请你与同伴交流并回答用的是什么方法.
3.李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB，但他随身只带了卷尺，（1）你能替他想办法完成任务吗？
（2）李叔叔量得AD长是30厘米，AB长是40厘米，BD长是50厘米，AD边垂直于AB边吗？为什么？
（3）小明随身只有一个长度为20厘米的刻度尺，他能有办法检验AD边是否垂直于AB边吗？BC边与AB边呢？
如图，一只蚂蚁从实心长方体的顶点A出发，沿长方体的表面爬到对角顶点C1处（三条棱长如图所示），问怎样走路线最短？最短路线长为多少？
1.一个直角三角形的两边长分别为3和4，则第三边长的平方为＿＿＿＿＿＿＿．2．直角三角形一直角边长为6cm，斜边长为10cm，则这个直角三角形的面积为＿＿＿＿，斜边上的高为＿＿＿＿＿，斜边上的中线是 ＿ ． 3．等腰△ABC的腰长为10cm，底边长为16cm，则底边上的高为＿＿，面积为______，腰上的高是 .
4．等腰直角△ABC中，∠C=90°，AC=2cm，那么它的斜边上的高的平方为＿＿＿．5.甲、乙两人同时从同一地点出发，甲往东走了4km，乙往南走了6km，这时甲、乙两人相距的平方__________km2．6.一张长方形纸片宽AB=8cm，长BC=10cm.现将纸片折叠，使顶点D落在BC边上的点F处(折痕为AE)，求EC的长．
解：由折叠可知AF=AD=10,DE=EF,在Rt △ABF中， ∠ B=90 ° ，所以AB2+BF2=AF2,BF=6.CF=4,设EC=X,则EF=DE=8-X,在Rt △EFC中， ∠ C=90 ° ，所以EC2+CF2=EF2,X2+42=(8-X) 2，X=24/9
　　从勾股定理的应用中我们进一步体会到直角三角形与等腰三角形有着密切的联系；把研究等腰三角形转化为研究直角三角形，这是研究问题的一种策略．
　勾股定理主要应用于求线段的长度、图形的周长、面积； 　勾股定理的逆定理用于判断三角形的形状．
1．如图，在△ABC中， AB＝AC＝17，BC＝16，求△ABC的面积．
2．如图，在△ABC中，AD⊥BC，AB＝15，AD＝12，AC＝13，求△ABC的周长和面积．
如图，以△ABC的三边为直径向外作半圆，且S1＋S3＝S2，试判断△ABC的形状？