人教A版 (2019)必修 第一册第三章 函数概念与性质3.2 函数的基本性质精品第二课时一课一练
展开一.选择题
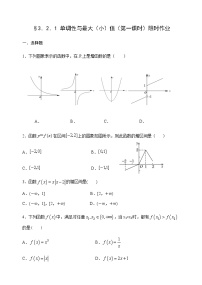
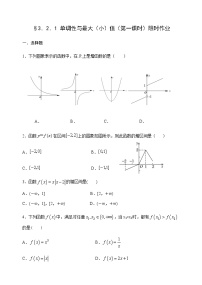
1.下列函数中,既是奇函数又是增函数的为( )
A.B.
C.D.
2.函数的减区间是( )
A.B.
C.,D.
3.函数的单调递增区间是( )
A.B.
C.D.
4.已知函数在上单调递增,则实数的取值范围是( )
A.B.
C.D.
5.函数的递增区间是______.
A.B.
C.D.
6.数学老师给出一个定义在R上的函数f(x),甲、乙、丙、丁四位同学各说出了这个函数的一条性质:
甲:在(-∞,0)上函数单调递减; 乙:在[0,+∞] 上函数单调递增;
丙:函数f(x)的图象关于直线x=1对称; 丁: f(0)不是函数的最小值.
老师说:你们四个同学中恰好有三个人说的正确,则说法错误的同学是( )
A.甲B.乙
C.丙D.丁
7.函数的单调递减区间为( )
A.B.
C.D.
8.若函数区间单调递减,则a的取值范围是( )
A.B.
C.D.
二.填空题
9.若函数的单调递增区间是,则=________.
10.的单调减区间是__________.
三.解答题
11.已知函数
(1)请在给定的坐标系中画出此函数的图象;
(2)写出此函数的定义域及单调区间,并写出值域.
12.若非零函数对任意实数均有,且当时,.
(1)求证:;
(2)求证:为减函数;
(3)当时,解不等式
§3.2.1 单调性与最大(小)值(第二课时)限时作业
【参考答案】
一.选择题
1.下列函数中,既是奇函数又是增函数的为( )
A.B.C.D.
【答案】D
2.函数的减区间是( )
A.B.
C.,D.
【答案】C
3.函数的单调递增区间是( )
A.B.
C.D.
【答案】B
4.已知函数在上单调递增,则实数的取值范围是( )
A.B.
C.D.
【答案】B
5.函数的递增区间是______.
A.B.
C.D.
【答案】A
6.数学老师给出一个定义在R上的函数f(x),甲、乙、丙、丁四位同学各说出了这个函数的一条性质:
甲:在(-∞,0)上函数单调递减; 乙:在[0,+∞] 上函数单调递增;
丙:函数f(x)的图象关于直线x=1对称; 丁: f(0)不是函数的最小值.
老师说:你们四个同学中恰好有三个人说的正确,则说法错误的同学是( )
A.甲B.乙C.丙D.丁
【答案】B
7.函数的单调递减区间为( )
A.B.C.D.
【答案】D
8.若函数区间单调递减,则a的取值范围是( )
A.B.C.D.
【答案】C
二.填空题
9.若函数的单调递增区间是,则=________.
【答案】
10.的单调减区间是__________.
【答案】
三.解答题
11.已知函数
(1)请在给定的坐标系中画出此函数的图象;
(2)写出此函数的定义域及单调区间,并写出值域.
【答案】
(1)图象如图所示:
(2)由函数的图象可知,该函数的定义域为,
增区间为,减区间为、、,值域为.
12.若非零函数对任意实数均有,且当时,.
(1)求证:;
(2)求证:为减函数;
(3)当时,解不等式
【答案】(1)
(2)设则
所以
为减函数.
(3)由
由(1)得
原不等式转化为,
结合(2)得:
即
故不等式的解集为.
高中数学人教A版 (2019)必修 第一册第三章 函数的概念与性质3.2 函数的基本性质当堂达标检测题: 这是一份高中数学人教A版 (2019)必修 第一册第三章 函数的概念与性质3.2 函数的基本性质当堂达标检测题,文件包含321单调性与最大小值原卷版-高中数学人教A版2019必修第一册docx、321单调性与最大小值解析版-高中数学人教A版2019必修第一册docx等2份试卷配套教学资源,其中试卷共17页, 欢迎下载使用。
数学必修 第一册3.2 函数的基本性质第一课时当堂达标检测题: 这是一份数学必修 第一册3.2 函数的基本性质第一课时当堂达标检测题,共15页。
人教A版 (2019)必修 第一册第三章 函数概念与性质3.2 函数的基本性质优秀练习题: 这是一份人教A版 (2019)必修 第一册第三章 函数概念与性质3.2 函数的基本性质优秀练习题,文件包含321单调性与最大小值解析版docx、321单调性与最大小值原卷版docx等2份试卷配套教学资源,其中试卷共91页, 欢迎下载使用。