高中数学3.2 函数的基本性质优质ppt课件

这是一份高中数学3.2 函数的基本性质优质ppt课件，共22页。PPT课件主要包含了新课引入，生活中的对称美，奇函数，偶函数，非奇非偶函数，既奇又偶函数，fx0x∈R，∴fx偶函数，∴fx奇函数，随堂练习等内容，欢迎下载使用。

前面我们用符号语言精确地描述了函数图像在定义域的某个区间上“上升”(或“下降”)的性质，下面我们研究函数的其他性质.
轴对称图形： 如果一个图形上的任意一点关于某一条直线的对称点仍是这个图形上的点，就称图形关于该直线成轴对称图形，这条直线称作轴对称图形的对称轴。
中心对称图形： 如果一个图形上的任意一点关于某 一点的对称点仍是这个图形上的点，就称图形关于该点成中心对称图形，这个点称作中心对称图形的对称中心。
观察下列各个函数的图象,你能说说它们分别反映了相应函数的哪些变化规律？请同学们畅所欲言。
在上面的函数图象中,这两个函数的图像都关于y轴对称.
类比函数单调性，如何用数学符号语言准确描述“函数图象关于y轴对称”的这种特征呢?
列出x,y的对应值表:
-1 1
∀x∈R，都有f(-x)=(-x)2=x2=f(x)
这时我们称f(x)=x2为偶函数.
函数f(x)=x2, x∈[-2,2]的图像关于y轴对称吗？它是偶函数吗？
函数f(x)=x2, x∈[-1,2]呢?
偶函数：一般地，设函数f(x)的定义域为I，如果①∀x∈I，-x∈I，②f(-x)=f(x)那么函数f(x)就叫做偶函数.
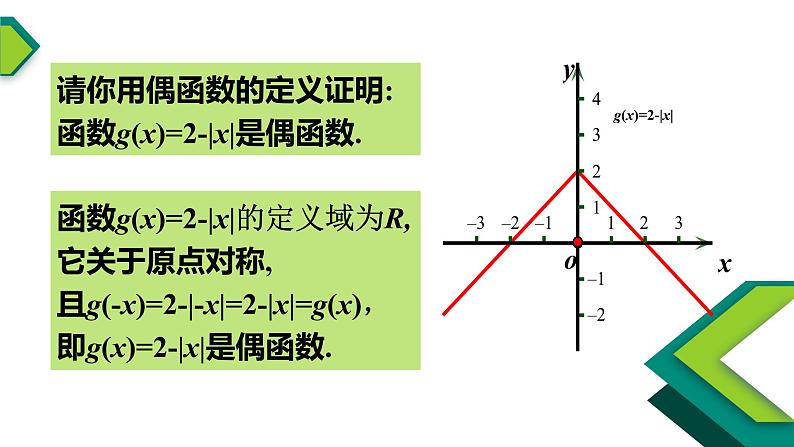
函数g(x)=2-|x|的定义域为R,它关于原点对称,且g(-x)=2-|-x|=2-|x|=g(x)，即g(x)=2-|x|是偶函数.
请你用偶函数的定义证明:函数g(x)=2-|x|是偶函数.
在上面的函数图象中,这两个函数的图像都关于原点对称.
类比函数单调性，如何用数学符号语言准确描述“函数图象关于原点对称”的这种特征呢?
∀x∈R，都有f(-x)=-x=-f(x)
这时我们称f(x)=x为奇函数.
函数f(x)=x, x∈[-2,2]的图像关于y轴对称吗？它是偶函数吗？
函数f(x)=x, x∈[-1,3]呢?
-4 -3 -2 -1 0 1 2 3 4
奇函数：一般地，设函数f(x)的定义域为I，如果①∀x∈I，-x∈I，②f(-x)=-f(x)那么函数f(x)就叫做奇函数.
根据奇偶性, 函数可划分为四类:
观察下列函数图像，并判断它们的奇偶性
P85 1.已知f(x)是偶函数，g(x)是奇函数，试将下图补充完整.
例6、判断下列函数的奇偶性：
(1)解：定义域为R，∵∀x∈R,都有-x∈R，且f(-x)=(-x)4=f(x)
(2)解：定义域为R，它关于原点对称，且 f(-x)=(-x)5=- x5 =-f(x)
(4)解：定义域为{x|x≠0} ，它关于原点对称
判断或证明函数奇偶性的基本步骤
③ f(x)=x5 ________
①f(x)=x4 _______ ④ f(x)= x -1 ________
说出下列函数的奇偶性:
② f(x)=x ________
⑤f(x)=x 2 ________
⑥f(x)=x 3 _____________
函数f(x)=x n 中 ：若n为偶数，则它为偶函数.若n为奇数，则它为奇函数.
奇函数，偶函数作一些简单运算后会出现一些规律： 奇+奇=奇 偶+偶=偶 奇×奇=偶 偶×偶=偶
判断函数的奇偶性的方法有：图像法和定义法
定义法步骤：①首先确定函数的定义域，并判断其定义域是否关于原点对称；②计算f(-x)，确定f(-x)与f(x)的关系；③作出相应结论。