初中数学北师大版八年级上册2 一次函数与正比例函数精品课件ppt

这是一份初中数学北师大版八年级上册2 一次函数与正比例函数精品课件ppt，共26页。PPT课件主要包含了学习目标，情景引入，y2x，y4x，ykx，y3+05x，y60－012x，练一练，方法总结，典例精析等内容，欢迎下载使用。

1.掌握一次函数、正比例函数的概念.（重点）2.能根据条件求出一次函数的关系式．（难点）
如果设蛤蟆的数量为x，y分别表示蛤蟆嘴的数量，眼睛的数量，腿的数量，扑通声，你能列出相应的函数解析式吗？
在现实生活当中有许多问题都可以归结为函数问题,大家能不能举一些例子?
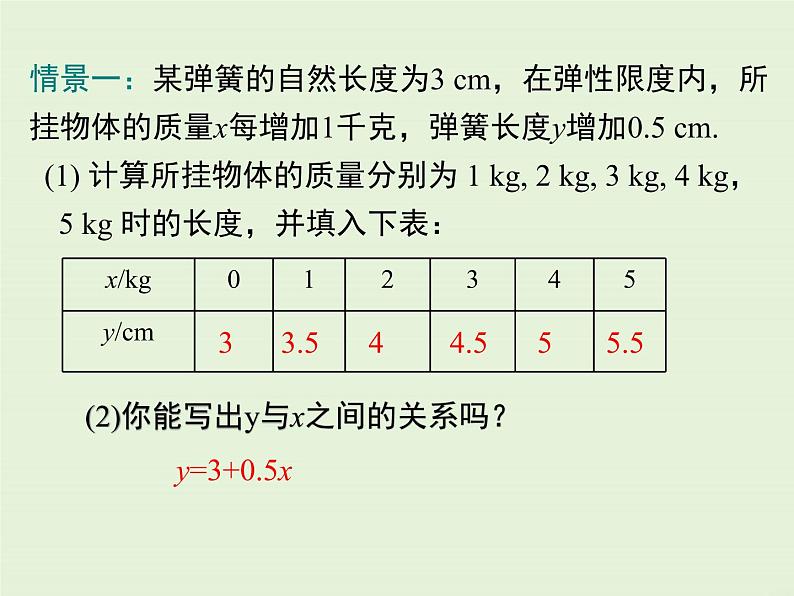
(2)你能写出y与x之间的关系吗？
情景一：某弹簧的自然长度为3 cm，在弹性限度内，所挂物体的质量x每增加1千克，弹簧长度y增加0.5 cm. (1) 计算所挂物体的质量分别为 1 kg, 2 kg, 3 kg, 4 kg， 5 kg 时的长度，并填入下表：
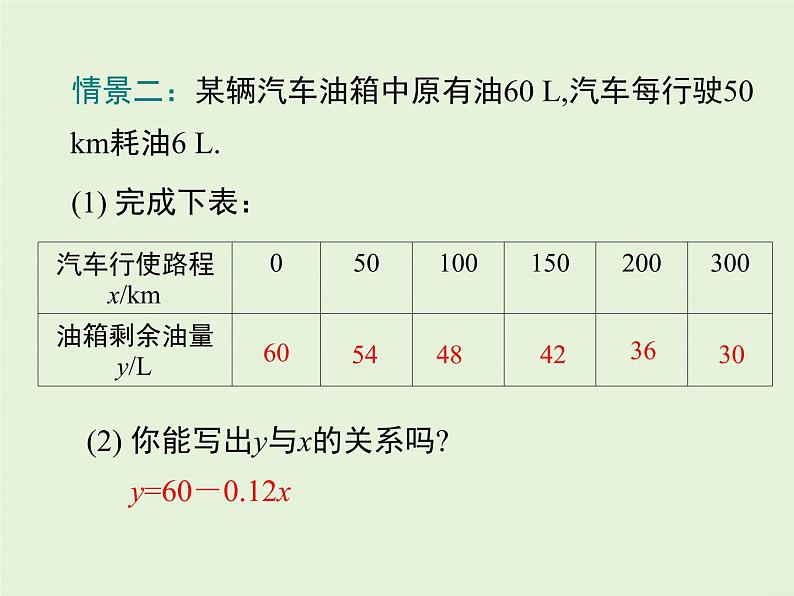
情景二：某辆汽车油箱中原有油60 L,汽车每行驶50 km耗油6 L. (1) 完成下表：
(2) 你能写出y与x的关系吗?
上面的两个函数关系式: (1)y=3+0.5x (2) y=60－0.12x
若两个变量 x、y之间的关系可以表示成y=kx+b(k,b为常数，k不等于0）的形式，则称 y是x的一次函数.（x为自变量，y为因变量.）
当b=0时，称y是x的正比例函数.
大家讨论一下,这两个函数关系式有什么关系?
下列关系式中，哪些是一次函数，哪些是正比例函数？ (1)y＝－x－4; (2)y＝5x2－6； (3)y＝2πx; (6)y＝8x2＋x(1－8x)
解：(1)是一次函数，不是正比例函数；(2)不是一次函数，也不是正比例函数；(3)是一次函数，也是正比例函数；(4)是一次函数，也是正比例函数；(5)不是一次函数，也不是正比例函数；(6)是一次函数，也是正比例函数．
1.判断一个函数是一次函数的条件：自变量是一次整式，一次项系数不为零；2.判断一个函数是正比例函数的条件：自变量是一次整式，一次项系数不为零，常数项为零．
例1：写出下列各题中y与 x之间的关系式，并判断：y是否为x的一次函数？是否为正比例函数？（1）汽车以60km/h的速度匀速行驶,行驶路程为y(km)与行驶时间x(h)之间的关系;
解：由路程=速度×时间，得y=60x ,y是x的 一次函数,也是x的正比例函数.
解：由圆的面积公式，得y=πx2, y不是x的正比例函数，也不是x的一次函数.
（2）圆的面积y (cm2 )与它的半径x (cm)之间的关系.
解：这个水池每时增加5m3水，x h增加5x m3水， 因而 y=15+5x, y是x的一次函数，但不是x的正比例函数.
（3）某水池有水15m3，现打开进水管进水，进水速度为5m3/h，x h后这个水池有水y m3.
例2：已知函数y＝(m－5)xm2－24＋m＋1.(1)若它是一次函数，求m的值；(2)若它是正比例函数，求m的值．
解：(1) 因为y＝(m－5)xm2－24＋m＋1是一次函数， 所以 m2－24＝1且m－5≠0， 所以 m＝±5且m≠5， 所以 m＝－5. 所以，当m＝－5时，函数y＝(m－5)xm2－24 ＋m＋1是一次函数．
(2)若它是正比例函数，求 m 的值．
解：(2)因为 y＝(m－5)xm2－24＋m＋1是一次函数， 所以 m2－24＝1且m－5≠0且m＋1＝0. 所以 m＝±5且m≠5且m＝－1， 则这样的m不存在， 所以函数y＝(m－5)xm2－24＋m＋1不可能为 正比例函数．
【方法总结】函数是一次函数，则k≠0，且自变量的次数为1.当b＝0时，一次函数为正比例函数．
(1)若 是正比例函数，则m= ；
(2)若 是正比例函数，则m= ；
m-2≠0， |m|-1=1，
m-1≠0， m2-1=0，
例3：我国现行个人工资、薪金所得税征收办法规定：月收入低于3500元的部分不收税；月收入超过3500元但低于5000元的部分征收3%的所得税……如某人月收入3860元,他应缴个人工资、薪金所得税为:（3860-3500）×3%=10.8元.
(1)当月收入大于3500元而又小于5000元时,写出应缴所得税y(元)与收入x(元)之间的关系式.
解: y=0.03×(x-3 500) (3500(2)某人月收入为4160元，他应缴所得税多少元？
解:当x=4160时，y=0.03×(4160-3500)=19.8（元）.
解:设此人本月工资是x元，则 19.2=0.03×(x-3500), x=4140. 答:此人本月工资是4140元.
(3)如果某人本月应缴所得税19.2元，那么此人本月工资是多少元？
如图，△ABC是边长为x的等边三角形.（1）求BC边上的高h与x之间的函数解析式.h是x的一次函数吗？如果是，请指出相应的k与b的值.
解: (1)∵BC边上的高AD也是BC边上的中线，∴BD= 在Rt△ABD中，由勾股定理，得
（3）求△ABC的面积S与x的函数解析式.S是x的一次函数吗？
1.判断:(1)y=2.2x，y是x的一次函数，也是x的正比例函数. （ ） (2)y=80x+100 ，y是x的一次函数. （ ）
2.在函数y=(m-2)x+(m2-4)中，当m 时，y是x的一次函数；当m 时，y时x的正比例函数.
3.已知函数y=(m-1)x｜m︱+1是一次函数，求m值；
4.若函数y=(m-3)x+m2-9是正比例函数，求m的值；
解：根据题意，得∣m∣=1,解得m=±1，但m-1≠0,即m≠1,所以m=-1.
解：根据题意，得m2-9=0,解得m=±3，但m-3≠0,即m≠3,所以m=-3.
5.已知y-3与x成正比例，并且x=4时，y=7，求
y与x之间的函数关系式.
解：依题意，设y-3与x之间的函数关系式为y-3=kx，
∵x=4时，y=7，∴7-3=4k，解得k=1.
∴y-3=x，即y=x+3.
6.有一块10公顷的成熟麦田，用一台收割速度为0.5公顷每小时的小麦收割机来收割.（1）求收割的面积y（单位：公顷）与收割时间x（单位：时）之间的函数关系式；（2）求收割完这块麦田需用的时间.
解：（1）y=0.5x；（2）把y=10代入y=0.5x中，得10=0.5x.解得x=20，即收割完这块麦田需要20小时.
　7.一个小球由静止开始沿一个斜坡向下滚动，其速度每秒增加2 m/s． （1）求小球速度v（单位：m/s）关于时间t（单位：s）的函数解析式;
解：小球速度v关于时间t的函数解析式为v=2t.
（2）求第2.5 s 时小球的速度； （3）时间每增加1 s，速度增加多少，速度增加量是否随着时间的变化而变化？
(2)当t=2.5时，v=2×2.5=5(m/s).
(3)时间每增加1 s，速度增加2 m/s，速度增加量不随着时间的变化而变化.