数学第十一章 三角形综合与测试课后练习题

这是一份数学第十一章 三角形综合与测试课后练习题，共9页。试卷主要包含了如图能说明∠1＞∠2的是等内容，欢迎下载使用。
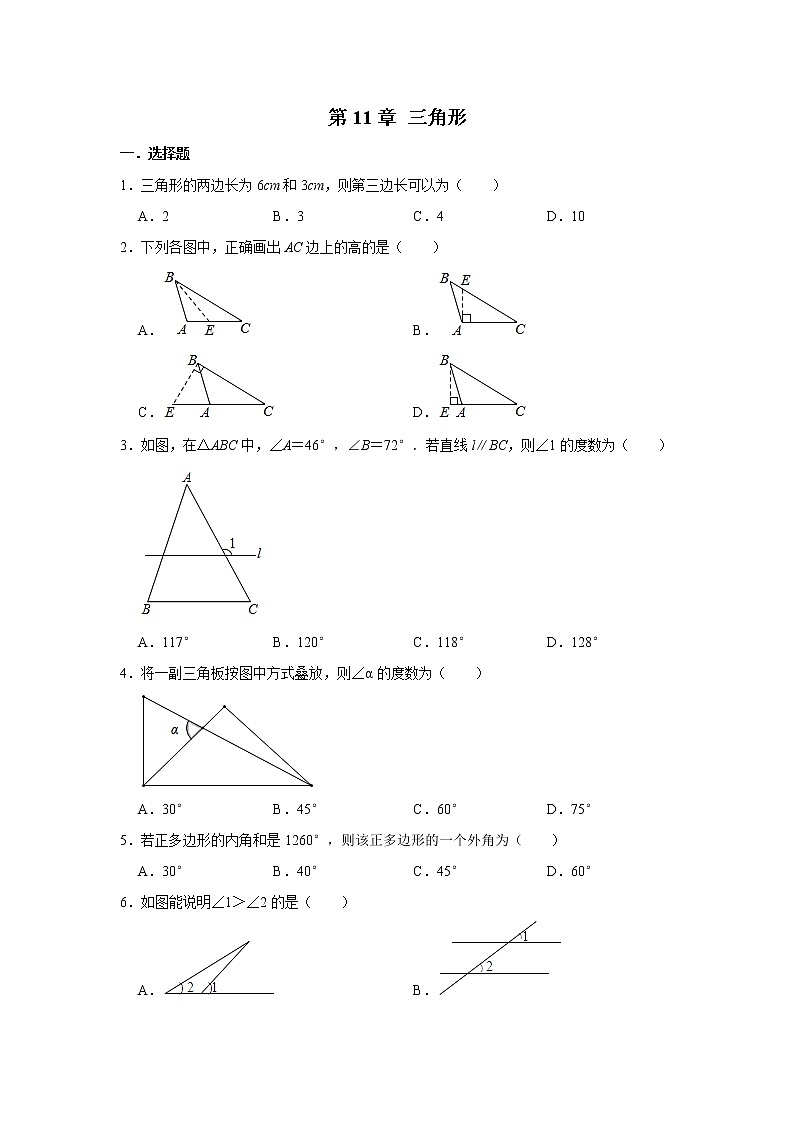
1．三角形的两边长为6cm和3cm，则第三边长可以为（ ）
A．2B．3C．4D．10
2．下列各图中，正确画出AC边上的高的是（ ）
A．B．
C．D．
3．如图，在△ABC中，∠A＝46°，∠B＝72°．若直线l∥BC，则∠1的度数为（ ）
A．117°B．120°C．118°D．128°
4．将一副三角板按图中方式叠放，则∠α的度数为（ ）
A．30°B．45°C．60°D．75°
5．若正多边形的内角和是1260°，则该正多边形的一个外角为（ ）
A．30°B．40°C．45°D．60°
6．如图能说明∠1＞∠2的是（ ）
A．B．
C．D．
7．将一副三角板如图放置，使点A落在DE上，AB与CE交于点F，若BC∥DE，则∠BFE的度数为（ ）
A．55°B．65°C．75°D．85°
8．如图，CD是直角△ABC斜边AB上的高，CB＞CA，图中相等的角共有（ ）
A．2对B．3对C．4对D．5对
9．如图所示，已知△ABC中，∠A＝80°，若沿图中虚线剪去∠A，则∠1+∠2等于（ ）
A．90°B．135°C．260°D．315°
10．下列多边形中，对角线是5条的多边形是（ ）
A．四边形B．五边形C．六边形D．七边形
二．填空题
11．如图，在线段AD，AE，AF中，△ABC的高是线段 ．
12．已知三角形的一个内角是（180﹣x）度，且最大角与最小角之差是24°，则x的最大可能值与最小可能值之和为 ．
13．如图，将一副直角三角板，按如图所示叠放在一起，则图中∠COB＝ ．
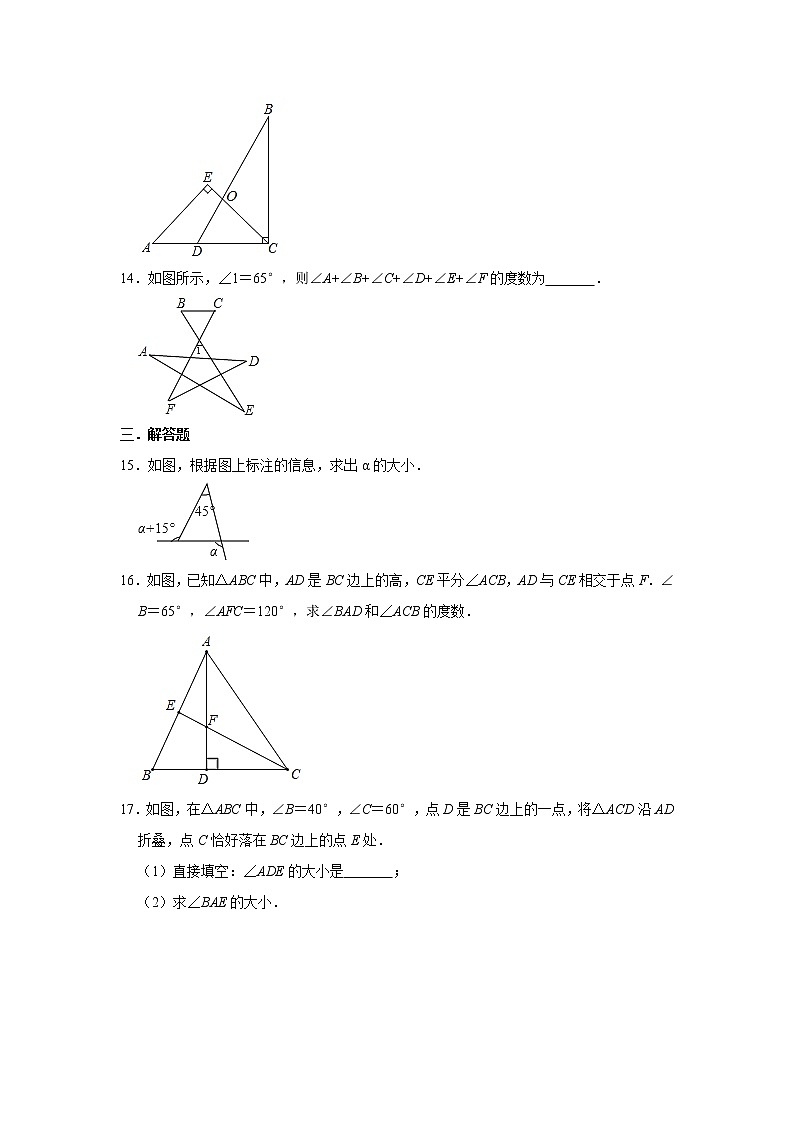
14．如图所示，∠1＝65°，则∠A+∠B+∠C+∠D+∠E+∠F的度数为 ．
三．解答题
15．如图，根据图上标注的信息，求出α的大小．
16．如图，已知△ABC中，AD是BC边上的高，CE平分∠ACB，AD与CE相交于点F．∠B＝65°，∠AFC＝120°，求∠BAD和∠ACB的度数．
17．如图，在△ABC中，∠B＝40°，∠C＝60°，点D是BC边上的一点，将△ACD沿AD折叠，点C恰好落在BC边上的点E处．
（1）直接填空：∠ADE的大小是 ；
（2）求∠BAE的大小．
18．阅读下面的材料，并解决问题．
（1）已知在△ABC中，∠A＝60°，图1﹣3的△ABC的内角平分线或外角平分线交于点O，请直接求出下列角度的度数．
如图1，∠O＝ ；如图2，∠O＝ ；如图3，∠O＝ ；
如图4，∠ABC，∠ACB的三等分线交于点O1，O2，连接O1O2，则∠BO2O1＝ ．
（2）如图5，点O是△ABC两条内角平分线的交点，求证：∠O＝90°+∠A．
（3）如图6，△ABC中，∠ABC的三等分线分别与∠ACB的平分线交于点O1，O2，若∠1＝115°，∠2＝135°，求∠A的度数．
19．如图，有两根竹竿AB、DB靠在墙角上，并与墙角FCE形成一定的角度，测得∠CAB，∠CDB的度数分别为α，β．用含有α，β的代数式表示∠DBF和∠ABD的度数．
参考答案
一．选择题
1． C．
2． D．
3． C．
4． D．
5． B．
6． A．
7． C．
8． D．
9．C．
10． B．
二．填空题
11． AF．
12． 240．
13． 105°．
14． 230°．
三．解答题
15．解：∵α+15＝45°+180°﹣α
∴α＝105°．
16．解：∵AD是BC边上的高，
∴∠ADB＝∠ADC＝90．
在△ABD中，∠BAD＝180°﹣∠ADB﹣∠B＝180°﹣90°﹣65°＝25°．
∵∠AFC是△CDF的外角，
∴∠AFC＝∠FDC+∠FCD，
∴∠FCD＝∠AFC﹣∠FDC＝120°﹣90°＝30°．
∵CE平分∠ACB，
∴∠ACB＝2∠FCD＝2×30°＝60°．
答：∠BAD的度数是25°，∠ACB的度数是60°．
17．解：（1）∵将△ACD沿AD折叠，点C恰好落在BC边上的点E处，
∴∠ADE＝∠ADC＝180°＝90°，
故答案为：90°；
（2）由图形折叠的性质可得：∠AED＝∠C＝60°，
∵∠AED＝∠B+∠BAE，
∴∠BAE＝∠AED﹣∠B＝60°﹣40°＝20°．
18．解；（1）如图1，
∵BO平分∠ABC，CO平分∠ACB
∴∠OBC＝∠ABC，∠OCB＝∠ACB
∴∠OBC+∠OCB
＝（∠ABC+∠ACB）
＝（180°﹣∠BAC）
＝（180°﹣60°）
＝60°
∴∠O＝180°﹣（∠OBC+∠OCB）＝120°；
如图2，
∵BO平分∠ABC，CO平分∠ACD
∴∠OBC＝∠ABC，∠OCD＝∠ACD
∵∠ACD＝∠ABC+∠A
∴∠OCD＝（∠ABC+∠A）
∵∠OCD＝∠OBC+∠O
∴∠O＝∠OCD﹣∠OBC
＝∠ABC+∠A﹣∠ABC
＝∠A
＝30°
如图3，
∵BO平分∠EBC，CO平分∠BCD
∴∠OBC＝∠EBC，∠OCB＝∠BCD
∴∠OBC+∠OCB
＝（∠EBC+∠BCD）
＝（∠A+∠ACB+∠BCD）
＝（∠A+180°）
＝（60°+180°）
＝120°
∴∠O＝180°﹣（∠OBC+∠OCB）＝60°
如图4，
∵∠ABC，∠ACB的三等分线交于点O1，O2
∴∠O2BC＝∠ABC，∠O2CB＝∠ACB，O1B平分∠O2BC，O1C平分∠O2CB，O2O1平分BO2C
∴∠O2BC+∠O2CB
＝（∠ABC+∠ACB）
＝（180°﹣∠BAC）
＝（180°﹣60°）
＝80°
∴∠BO2C＝180°﹣（∠O2BC+∠O2CB）＝100°
∴∠BO2O1＝∠BO2C＝50°
故答案为：120°，30°，60°，50°；
（2）证明：∵OB平分∠ABC，OC平分∠ACB，
∴∠OBC＝∠ABC，∠OCB＝∠ACB，
∠O＝180°﹣（∠OBC+∠OCB）
＝180°﹣（∠ABC+∠ACB）
＝180°﹣（180°﹣∠A）
＝90°+∠A．
（3）∵∠O2BO1＝∠2﹣∠1＝20°
∴∠ABC＝3∠O2BO1＝60°，∠O1BC＝∠O2BO1＝20°
∴∠BCO2＝180°﹣20°﹣135°＝25°
∴∠ACB＝2∠BCO2＝50°
∴∠A＝180°﹣∠ABC﹣∠ACB＝70°
或由题意，设∠ABO2＝∠O2BO1＝∠O1BC＝α，∠ACO2＝∠BCO2＝β，
∴2α+β＝180°﹣115°＝65°，α+β＝180°﹣135°＝45°
∴α＝20°，β＝25°
∴∠ABC+∠ACB＝3α+2β＝60°+50°＝110°，
∴∠A＝70°．
19．解：∠DBF＝90°+β；
∠ABF＝90°+α，
所以∠ABD＝∠ABF﹣∠DBF＝α﹣β．