人教A版 (2019)选择性必修 第一册第一章 空间向量与立体几何1.2 空间向量基本定理精练

这是一份人教A版 (2019)选择性必修 第一册第一章 空间向量与立体几何1.2 空间向量基本定理精练，文件包含12空间向量基本定理原卷版docx、12空间向量基本定理解析版docx等2份试卷配套教学资源，其中试卷共26页， 欢迎下载使用。

思维导图





新课标要求


了解空间向量基本定理及其意义，掌握空间向量的正交分解。





知识梳理


定理：如果三个向量a，b，c不共面，那么对空间任一向量p，存在有序实数组{x，y，z}，使得p＝xa＋yb＋zc，其中{a，b，c}叫做空间的一个基底，a，b，c都叫做基向量．





名师导学


知识点1 基底与基向量


【例1-1】有以下命题：如果向量与任何向量不能构成空间向量的一组基底，那么的关系是不共线；为空间四点，且向量不构成空间的一个基底，则点一定共面；已知向量是空间的一个基底，则向量也是空间的一个基底其中正确的命题是


A. B. C. D.


【变式训练1-1】已知向量是空间的一个基底，下列能构成空间的另一个基底的是


A. B.


C. D.








知识点2 空间向量基本定理及其应用


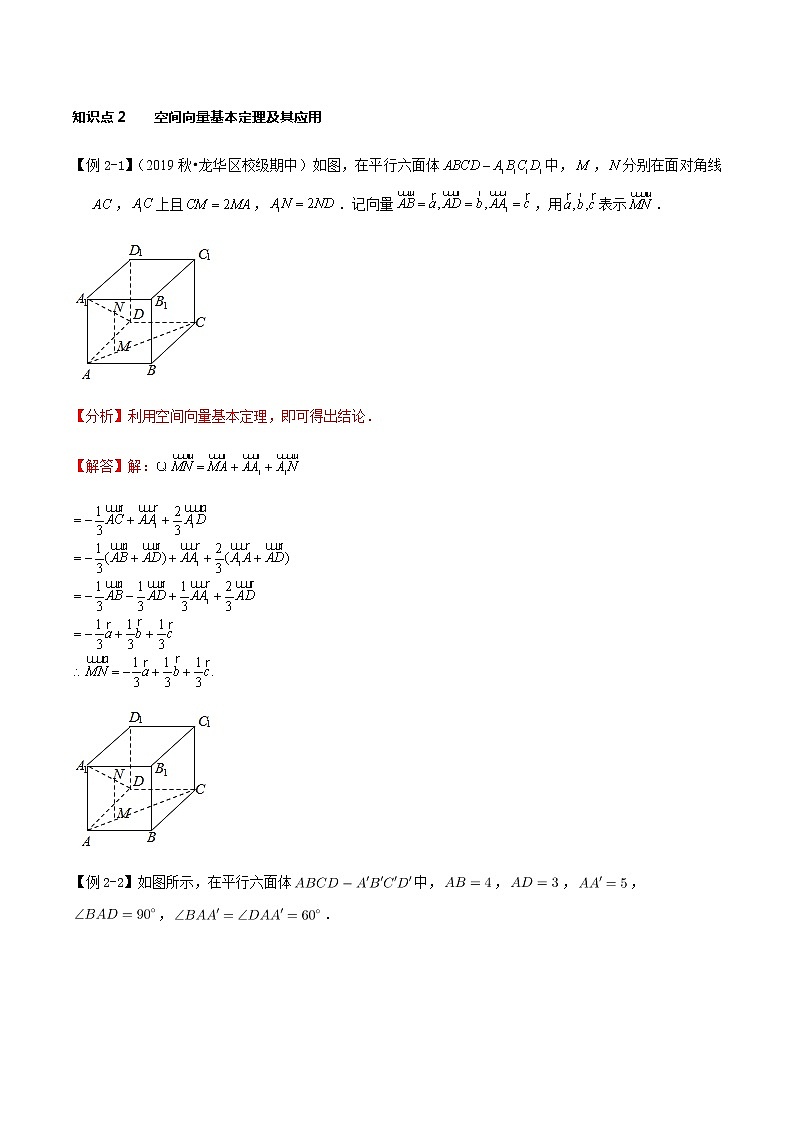
【例2-1】（2019秋•龙华区校级期中）如图，在平行六面体中，，分别在面对角线，上且，．记向量，用表示．




















【例2-2】如图所示，在平行六面体中，，，，，．





求的长；


求与的夹角的余弦值．

















【变式训练2-1】如图，四棱锥P－OABC的底面为一矩形，PO⊥平面OABC，设eq \(OA,\s\up6(→))＝a，eq \(OC,\s\up6(→))＝b，eq \(OP,\s\up6(→))＝c，E，F分别为PC和PB的中点，试用a，b，c表示eq \(BF,\s\up6(→))，eq \(BE,\s\up6(→))，eq \(AE,\s\up6(→))，eq \(EF,\s\up6(→)).




















【变式训练2-2】如图所示，已知空间四边形ABCD的每条边和对角线长都等于1，点E，F，G分别是AB，AD，CD的中点．





求


求EG的长．
































名师导练


A组-[应知应会]


1.若向量，，是空间的一个基底，向量，，那么可以与，构成空间的另一个基底的向量是


A. B. C. D.


2.（2019秋•东城区期末）在四面体中，点在上，且，为中点，则等于





A．B．


C．D．


3．（2019秋•菏泽期末）如图，已知正方体中，点为上底面的中心，若则





A．B．1C．D．2


4．（2019秋•济宁期末）如图所示，在平行六面体中，为与的交点，若，则





A．B．C．D．


5．（2019秋•阳泉期末）如图，在四面体中，是的中点，是的中点，则等于





A．B．


C．D．


6．（2019秋•烟台期末）三棱柱中，底面边长和侧棱长都相等，，则异面直线与所成角的余弦值为


A. B. C. D.


7．（多选）（2019秋•南通期末）设，，是空间一个基底


A．若，，则


B．则，，两两共面，但，，不可能共面


C．对空间任一向量，总存在有序实数组，，，使


D．则，，一定能构成空间的一个基底


8．（2019秋•邯郸期末）如图，在四棱柱中，底面是平行四边形，点为的中点，若，则 ．





9.已知四棱柱的底面ABCD是矩形，底面边长和侧棱长均为2，，则对角线的长为_____________．


10.已知为空间的一个基底，且，，，能否以作为空间的一个基底______ 填“能”或“不能”．


11．（2019秋•兴庆区校级期中）如图所示，已知空间四边形的每条边和对角线都等于1，点，，分别是，，的中点，设


，，，为空间向量的一组基底，


计算：


（1）；


（2）．























12．（2019秋•三门县校级期中）如图，在平行六面体中，，，，，，设，，．


（1）用，，表示；


（2）求的长．

















13.如图，在空间四边形OABC中，已知E是线段BC的中点，G在AE上，且．





试用向量，，表示向量；


若，，，，，求异面直线OG与AB所成角的余弦值．


B组-[素养提升]


1.已知平行六面体的底面ABCD是菱形，且，如图所示，则当的值为多少时，平面并给予证明．