

初中数学人教版八年级上册14.1 整式的乘法综合与测试优秀教学设计
展开第10讲
讲
整式乘法
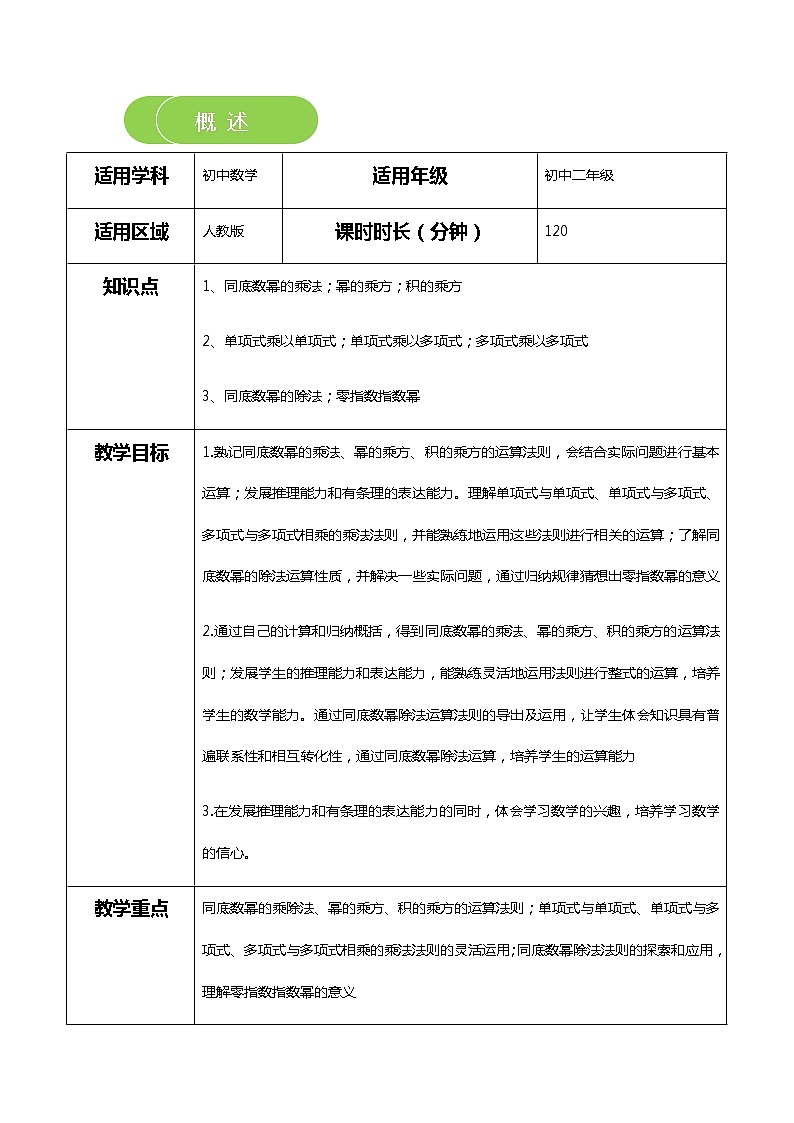
概 述
【知识导图】
教学过程
一、导入
复习预习
1.求n个相同因数的积的运算,叫做乘方,乘方的结果叫做幂。例如an这个表达式中,a是底数,n是指数,an又读作a的n次幂
2.乘方的性质:负数的偶次幂是正数,负数的奇次幂是负数,正数的任何次幂都是正数,0的任何正整数次幂都是零,例如(-1)2=1,(-1)-1=-1等
二、知识讲解
考点1
同底数幂的乘法法则:一般地,对于任何底数a与任何正整数m、n,
=因此我们有am﹒an=am+n(m,n都是正整数)
即同底数幂相乘,底数不变,指数相加。
注意:(1)三个或三个以上同底数幂相乘,法则也适用。即am×an×﹒﹒﹒×ap=am+n+﹒﹒﹒+p
(m,n,...,p都是正整数)
(2)不要忽略指数为1的因数
(3)底数不一定只是一个数字或一个字母
注意法则的逆用,即am+n=am﹒an(m,n都是正整数)
考点2
幂的乘方的的意义:幂的乘方是指几个相同的幂相乘。
幂的乘方法则:一般的,对于任意底数a与任意正整数m,n,因此,我们有(am)n=amn(m,n都是正整数)
即幂的乘方,底数不变,指数相乘。
注意:(1)法则可推广为[(am)n]p=amnp(m,n,p都是正整数)
(2)此法则可以逆用amn=(am)n=(an)m(m,n都是正整数)
考点3
积的乘方法则:一般的,对于任意底数a,b与任意正整数n,
因此,可得出(ab)n=anbn(n是正整数)
即积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘。
注意:(1)三个或三个以上因式的积的乘方,也具有这一性质.例如(abc)n=anbncn
(2)此法则可逆用:anbn=(ab)n
考点4
发现、总结
1.问题:光的速度约为3×105千米/秒,太阳光照射到地球上需要的时间大约是5×102秒,你知道地球与太阳的距离约是多少千米吗?
解答:(3×105 )×(5×102 )=(3×5)×(105 ×102 )=15×107
如果将上式中的数字改为字母,即ac5·bc2,我们可以得到
ac5·bc2 =(a·c5)·(b·c2) =(a·b)·(c5·c2) =abc5+2=abc7根据上式总结出单项式与单项式相乘的方法
2.问题:三家连锁店以相同的价格m(单位:元/瓶)销售某种商品,它们在一个月内的销售量(单位:瓶),分别是a,b,c。请用不同方法计算它们在这个月内销售这种商品的总收入
一种方法是先求三家连锁店的总销售量,再求总收入,即总收入为m(a+b+c),另一种方法是先分别求三家连锁店的收入,再求它们的和,即总收入为ma+mb+mc,所以:
m(a+b+c)= ma+mb+mc ,根据上式总结出单项式与多项式相乘的方法
3.问题:为了扩大绿地面积,要把街心花园的一块长a米,宽m米的长方形绿地增长b米,加宽n米,求扩地以后的面积是多少?用两种方法表示扩大后绿地的面积。
方法一:这块花园现在长(a+b)米,宽(m+n)米,因而面积为(a+b)(m+n)米2.
方法二:这块花园现在是由四小块组成,它们的面积分别为:am米2、an米2、bm米2、bn米2,故这块绿地的面积为(am+an+bm+bn)米2. (a+b)(m+n)和(am+an+bm+bn)表示同一块绿地的面积,(a+b)(m+n)=am+an+bm+bn,根据上式总结出多项式与多项式相乘的方法
考点5
结合以上情形,我们可以得到单项式与单项式、单项式与多项式、多项式与多项式相乘的乘法法则,即
1.单项式与单项式相乘的乘法法则:单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
2.单项式与多项式相乘的乘法法则:单项式与多项式相乘,就是先用单项式去乘多项式的每一项,再把所得的积相加。用式子表示为m(a+b+c)= ma+mb+mc(m,a,b,c都是单项式)
3.多项式与多项式相乘的乘法法则: 多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。用式子表示为(a+b)(m+n)=am+an+bm+bn
考点6
同底数幂的除法法则:一般地,我们有am÷an=am-n(a≠0,m,n都是正整数,并且m>n)
即同底数幂相除,底数不变,指数相减。
注意:
(1)底数a可以是单项式,也可以是多项式,但底数a不能为0,则除数为零,除法就没有意义了
(2)当三个或三个以上同底数幂相除时,也具有这一性质,例如am÷an÷ap=am-n-p(a≠0,m,n,p是正整数,并且m>n+p)
(3)应用这一法则时,必须明确底数是什么,指数是什么,然后按照同底数幂除法法则进行计算
(4)同底数幂的除法和同底数幂的乘法是互为逆运算
考点7
零指数幂的性质:同底数幂相除,如果被除式的指数等于除式的指数,例如am÷am,根据除法的意义可知所得的商为1,另一方面,如果按照同底数幂的除法来计算,又有am÷am=am-m
=a0
于是规定:a0=1(a≠0)
即任何不等于0的数的0次幂都等于1
注意:任何一个常数都可以看作与字母0次方的积,因此常数项可以看作是0次单项式
三 、例题精析
类型一 同底数幂相乘
例题1
计算(1)104×102 (2)(-b)3×(-b)2(3)xm+2﹒xm+1﹒xm﹒x
【答案】(1)104×102=104+2=106
(2)(-b)3×(-b)2=(-b)3+2=(-b)5
(3)xm+2﹒xm+1﹒xm﹒x=xm+2+m+1+m+1=x3m+4
【解析】三个题中,每个题中幂的底数都相同,根据同底数幂的运算法则同底数幂相乘,底
数不变,指数相加计算即可。
例题2
计算(1)(a+3)﹒(a+3)2﹒(a+3)5(2)(-x)﹒x2﹒(-x)3(3)(2a-3b)3﹒(3b-2a)4
【答案】(1)(a+3)﹒(a+3)2﹒(a+3)5=(a+3)1+2+5=(a+3)8
(2)(-x)﹒x2﹒(-x)3=-y﹒y2﹒(-y3)=y1+2+3=y6
(3)(2a-3b)3﹒(3b-2a)4=(2a-3b)3﹒(2a-3b)4=(2a-3b)3+4=(2a-3b)7
【解析】题(1)中把a+3看成一个整体,同样适用于同底数幂的乘法法则;题(2)中第二个
幂的底数与其它两个互为相反数,通过幂的运算转化为同底数后后进行计算;题(3)同题(2)一样底数互为相反数,通过幂的乘方符号法则转化运算转化成同底数幂后运用同底数
幂的运算法则进行计算。
注意:(1)同底数幂相乘时,底数可以是单项式,也可以是多项式
(2)幂的运算中经常用到的变形
,
例题3
(1)若am=2,an=5,则am+n=________.(2)已知3y=4,则3y+2=_______.
【答案】(1)am=2,an=5,am+n=am﹒an=2×5=10
(2)3y=4,则3y+2=3y﹒32=4×9=36
【解析】此例题运用了同底数幂的乘法法则,将所求转化为同底数幂的乘法然后整体代入求
值,体现了整体思想的应用。
类型二 幂的乘方
例题4
计算(1)(a2)3 (2)(xm-1)3 (3)[(-y)4]5
【答案】(1)(a2)3=a2×3=a6
(2)(xm-1)3 =x3(m-1)=x3m-3
(3)[(-y)4]5 =(-x)4×5=(-x)20=x20
【解析】根据幂的乘方法则,幂的乘方,底数不变,指数相乘计算即可
例题5
已知am=2,求a2m-a4m的值。
【答案】a2m-a3m==22-23=4-8=-4
【解析】此题逆用幂的乘方法则,将a2m-a3m转化为(am)2-(am)3后,把am=2整体代入求值即
可解答。
例题6
计算(1)(-2a2b)2 (2)-(-3xy2)4 (3)(-a3b2)3
【答案】(1)(-2a2b)2 =(-2)2﹒(a2)2﹒b2=4a4b2
(2)-(-3xy2)4 =-(-3)4﹒x4﹒(y2)4=-81x4y8
(3)(-a3b2)3=(-1)3﹒(a3)3﹒(b2)3=-a9b6
【解析】按照积的乘方的运算法则,把积中的每一个因式分别乘方即可。
类型三 积的乘方
例题7
计算(1)46×(0.25)6 (2)
【答案】(1)46×(0.5)6 =(4×0.25)6=16=1
(2)==(-1)1013=-1
【解析】此题若先算乘方,运算量太大,注意到4×0.25=1,,即
两底数的积容易求出.而指数又是相同的,故可逆用积的乘方的法则简便计算。
类型四 单项式乘单项式
例题8
计算(1)3x2﹒4x (2)2xy2﹒6x2y
【答案】(1)3x2﹒4x=3×4﹒x2+1=12x3
(2)2xy2﹒6x2y=2×6﹒x1+2y2+1=12x3y3
例题9
【解析】直接运用单项式与单项式相乘的乘法法则计算即可。
计算(1)(-xy2z3)2﹒(-x2y)3 (2)(2x3y)2﹒x3y+(-4x6)(-xy)3
【答案】(1)(-xy2z3)2﹒(-x2y)3 =x2y4z6﹒(-1)x6y3=-x8y7z6
(2)(2x3y)2﹒x3y+(-4x6)(-xy)3=4x6y2﹒x3y+(-4)﹒x6﹒(-1)﹒x3y3=4x9y3+4x9y3=8x9y3
【解析】先根据积的乘方法则进行计算,再直接运用单项式与单项式相乘的乘法法则计算,题(2)最后还要合并同类项
类型五 单项式乘多项式
例题10
计算(1)3x(x-1) (2)2x(3a+4b) (3)(x2y-2xy+y2)﹒(4xy)
【答案】(1)3x(x-1)=3x2-3x
(2)2x(3a+4b)=6xa+8xb
(3)(x2y-2xy+y2)﹒(4xy)=4x3y2-8x2y2+4xy3
【解析】直接运用单项式与多项式相乘的乘法法则计算即可
类型六 多项式乘多项式
例题11
计算(1)(3a+1)(a-3) (2)(2a+b)(a-2b) (3)(x-y)(x2+xy+y2)
【答案】(1)(3a+1)(a-3)=3a2-9a+a-3= 3a2-8a-3
(2)(2a+b)(a-2b)=2a2-4ab+ab-2b2=2a2-3ab-2b2
(3)(x-y)(x2+xy+y2)=x3+x2y+xy2-x2y-xy2-y3=x3-y3
【解析】首先运用多项式与多项式相乘的乘法法则计算,最后一定注意合并同类项
例题12
计算:
①; ②;
③; ④.
【答案】①;②;③;④.
【解析】根据同底数幂的除法法则即同底数幂相除,底数不变,指数相减计算即可。
例题13
计算(1)(x-2y)5÷(2y-x)2 (2)(-a)5÷a2 (3)(-ab)4÷(-a2b2)
【答案】(1)(x-2y)5÷(2y-x)2=)(x-2y)5÷(x-2y)2=(x-2y)5-2=(x-2y)3
(2)(-a)5÷a2=-a5÷a2=-a3
(3)(-ab)4÷(-a2b2)=(ab)4÷[-(ab)2]=-(ab)4-2=-(ab)2=-a2b2
例题14
【解析】底数不同,通过幂的乘方符号法则转化为同底数幂,再根据同底数幂的除法法则进行计算
若式子(x-2)0有意义,求x的取值范围
【答案】x-2≠0,x≠2
【解析】由零指数幂的意义可知,只要底数不等于零即可
例题15
已知ax=6,ay=2,求ax-y,a2x-y.
【答案】ax-y=ax÷ay=6÷2=3 a2x-y=a2x÷ay=(ax)2÷ay=62÷2=36÷2=18
【解析】根据同底数幂的除法的逆用及幂的乘方法则即可计算出结果
例题16
若,求的值.
【答案】∵32﹒(32)2a+1÷(33)a+1=32﹒34a+2÷33a+3=32+4a+2-3a-3=3a+1=81=34∴a+1=4∴a=3
【解析】等式左边底数都不相同,首先转化成同底数幂的形式,再根据同底数幂的乘法和除法法则进行计算,等式右边转化成与左边同底数的形式列出等量关系解答出结果。
四 、课堂运用
基础
1、计算:(1);(2);(3)
2、计算:(1);(2);(3) ;(4)
3、计算:(1);(2);(3)
答案与解析
【答案】1解:(1)
(2)
(3)
2 解:(1)
(2)
(3)
(4)
3解:(1)
(2)
(3)
提升
1、计算:(1);(2)
2、计算(1);(2)
3、计算:
答案与解析
【答案】 1解:(1)
2)
(2)
3
拔高
1、计算:(1);(2);
(3);(4)
2、计算:(1);(2);(3)(用简便运算)
3、计算:(1);(2)
答案与解析
【答案】1、解:(1)
(2)
(3)
(4)
2、解:(1)
(2)
(3)
3、解:(1)
(2)
五、课堂小结
1.同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,即am﹒an=am+n(m,n都是正整数)
2.幂的乘法法则:即幂的乘方,底数不变,指数相乘,即(am)n=amn(m,n都是正整数),
3.积的乘方法则:积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘,即(ab)n=anbn(n是正整数)
六、课后作业
基础
1.下列计算正确的是( )
A.x+x=2x2B.x3•x2=x5C.(x2)3=x5D.(2x)2=2x2
2.先化简,再求值:(x-1)(x+1)-x(x-3),其中x=3.
3.(1);(2)
答案与解析
【答案】1、解:A、x+x=2x≠2x2,故本选项错误;B、x3•x2=x5,故本选项正确;C、(x2)3=x6≠x5,故本选项错误;
D、(2x)2=4x2≠2x2,故本选项错误.故选:B.
2、解:原式=x2-1-x2+3x=3x-1,当x=3时,原式=9-1=8.
3、解
巩固
已知x-y=2,y-z=2,x+z=14,求x2-z2的值
3.
答案与解析
【答案】
1、解:因为x-y=2,y-z=2,将两式相加得x-z=4,所以x2-z2=(x+z)(x-z)=14×4=56.
2、
3、
拔高
1.为了交通方便,在一块长为am,宽为bm的长方形稻田内修两条道路,横向道路为矩形,纵向道路为平行四边形,道路的宽均为1m(如图),则余下可耕种土地的面积是_______________m2.
2.请看杨辉三角(1),并观察下列等式(2):
根据前面各式的规律,则(a+b)6=.
答案与解析
【答案】1、解答:.
2、解答:a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6.
七 、教学反思
适用学科
初中数学
适用年级
初中二年级
适用区域
人教版
课时时长(分钟)
120
知识点
1、同底数幂的乘法;幂的乘方;积的乘方
2、单项式乘以单项式;单项式乘以多项式;多项式乘以多项式
3、同底数幂的除法;零指数指数幂
教学目标
1.熟记同底数幂的乘法、幂的乘方、积的乘方的运算法则,会结合实际问题进行基本运算;发展推理能力和有条理的表达能力。理解单项式与单项式、单项式与多项式、多项式与多项式相乘的乘法法则,并能熟练地运用这些法则进行相关的运算;了解同底数幂的除法运算性质,并解决一些实际问题,通过归纳规律猜想出零指数幂的意义
2.通过自己的计算和归纳概括,得到同底数幂的乘法、幂的乘方、积的乘方的运算法则;发展学生的推理能力和表达能力,能熟练灵活地运用法则进行整式的运算,培养学生的数学能力。通过同底数幂除法运算法则的导出及运用,让学生体会知识具有普遍联系性和相互转化性,通过同底数幂除法运算,培养学生的运算能力
3.在发展推理能力和有条理的表达能力的同时,体会学习数学的兴趣,培养学习数学的信心。
教学重点
同底数幂的乘除法、幂的乘方、积的乘方的运算法则;单项式与单项式、单项式与多项式、多项式与多项式相乘的乘法法则的灵活运用;同底数幂除法法则的探索和应用,理解零指数指数幂的意义
教学难点
同底数幂的乘除法、幂的乘方、积的乘方的综合应用;多项式与多项式相乘的乘法法则的运用;理解零指数指数幂的意义
初中数学人教版八年级上册15.3 分式方程精品教学设计: 这是一份初中数学人教版八年级上册15.3 分式方程精品教学设计,共21页。教案主要包含了教学建议,知识导图,总结与反思等内容,欢迎下载使用。
数学八年级上册15.2 分式的运算综合与测试优质教案: 这是一份数学八年级上册15.2 分式的运算综合与测试优质教案,共20页。教案主要包含了教学建议,知识导图,总结与反思等内容,欢迎下载使用。
数学八年级上册15.1 分式综合与测试获奖教案: 这是一份数学八年级上册15.1 分式综合与测试获奖教案,共21页。教案主要包含了教学建议,知识导图,总结与反思等内容,欢迎下载使用。













