





数学24.1.2 垂直于弦的直径评课课件ppt
展开1.理解圆的轴对称性及垂径定理的推证过程;能初步应用垂径定理进行计算和证明;2.进一步培养学生观察问题、分析问题和解决问题的能力;3.通过圆的对称性,培养学生对数学的审美观,并激发学生对数学的热爱.
问题:你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥,是我国古代人民勤劳与智慧的结晶,它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4 m,拱高(弧的中点到弦的距离)为7.2 m,你能求出赵州桥主桥拱的半径吗?
想一想:将一个圆沿着任一条直径对折,两侧半圆会有什么关系?【解析】圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,所以两侧半圆折叠后重叠.
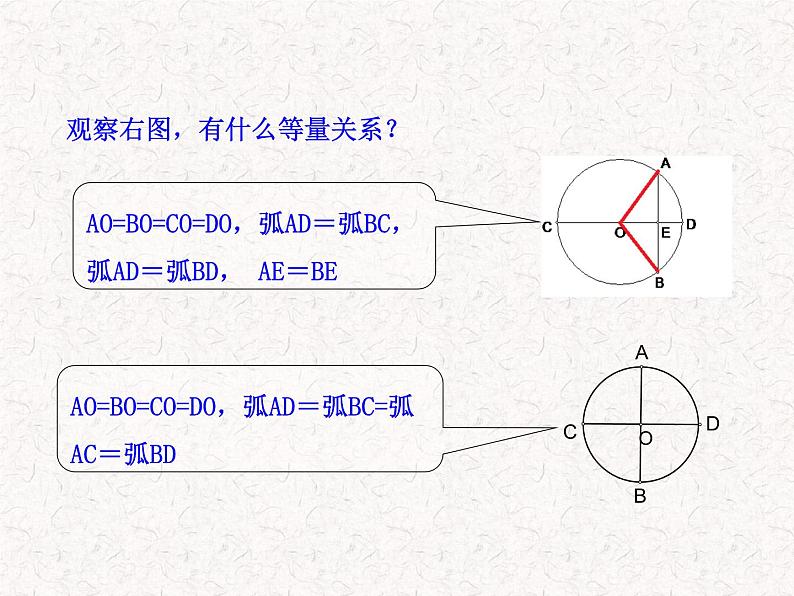
观察右图,有什么等量关系?
AO=BO=CO=DO,弧AD=弧BC,弧AD=弧BD, AE=BE
AO=BO=CO=DO,弧AD=弧BC=弧AC=弧BD
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E.求证:AE=BE,弧AC=弧BC,弧AD=弧BD.
垂径定理 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
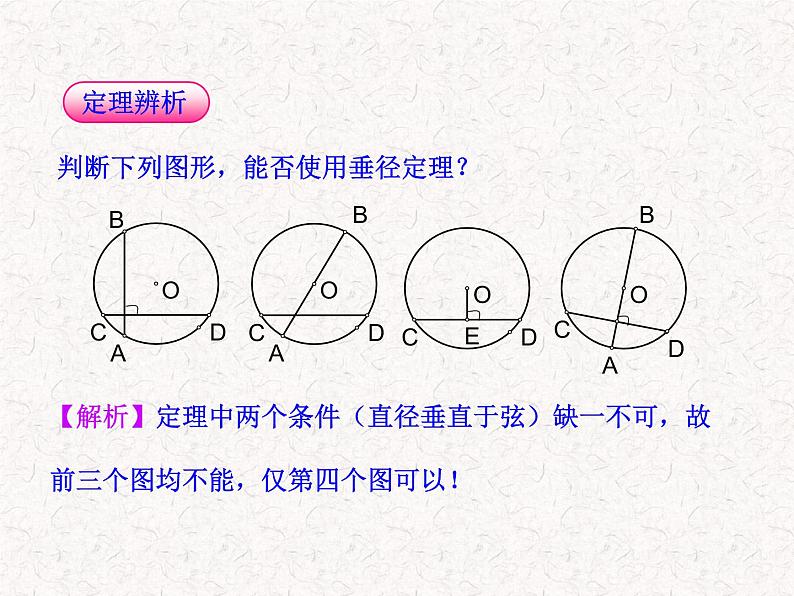
判断下列图形,能否使用垂径定理?
【解析】定理中两个条件(直径垂直于弦)缺一不可,故前三个图均不能,仅第四个图可以!
例1:如图,已知在圆O中,弦AB的长为8㎝,圆心O到AB的距离为3 ㎝,求圆O的半径。
【解析】根据题意得,AE=4cm OE⊥AB OE=3cm在Rt△OEA中,根据勾股定理得:AO2=OE2+AE2=32+42=25AO=5cm
如图,P为⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径.
关于弦的问题,常常需要过圆心作弦的垂线段,这是一条非常重要的辅助线.
【解析】提示作OM 垂直于PB ,连接OA.
画图叙述垂径定理,并说出定理的题设和结论.
想一想:如果将题设和结论中的5个条件适当互换,情况会怎样?
(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径,垂直平分弦并且平分弦所对的另一条弧.
如图,CD为⊙O的直径,AB⊥CD,EF⊥CD,你能得到什么结论?
圆的两条平行弦所夹的弧相等.
2.(湖州·中考)如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( )
A.AE=OE B.CE=DE
1.(绍兴·中考)已知⊙O的半径为5,弦AB的弦心距为3,则AB的长是( )A.3 B.4 C.6 D.8
3.(安徽·中考)如图,⊙O过点B 、C。圆心O在等腰直角△ABC的内部,∠BAC=900,OA=1,BC=6,则⊙O的半径为( )A. B. C. D. 【解析】选D.延长AO交BC于点D,连接OB,根据对称性知AO⊥BC,则BD=DC=3. 又△ABC为等腰直角三角形,∠BAC=90°,则AD= =3,∴OD=3-1=2,∴OB=
4.(毕节·中考)如图,AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,交⊙O于点C,且CD=l,则弦AB的长是 .
5、已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点.求证:AC=BD.证明:过O作OE⊥AB,垂足为E,则AE=BE,CE=DE.AE-CE=BE-DE.所以,AC=BD
初中数学人教版九年级上册24.1.2 垂直于弦的直径完整版课件ppt: 这是一份初中数学人教版九年级上册24.1.2 垂直于弦的直径完整版课件ppt,文件包含2412《垂直于弦的直径》课件--人教版数学九上pptx、2412《垂直于弦的直径》教案--人教版数学九上docx等2份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.2 垂直于弦的直径课堂教学ppt课件: 这是一份人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.2 垂直于弦的直径课堂教学ppt课件,共14页。PPT课件主要包含了学习目标,重点难点,预习导学,自学指导,自学检测,合作探究,小组合作,跟踪练习,课堂小结等内容,欢迎下载使用。
初中数学人教版九年级上册24.1.2 垂直于弦的直径多媒体教学ppt课件: 这是一份初中数学人教版九年级上册24.1.2 垂直于弦的直径多媒体教学ppt课件,共16页。PPT课件主要包含了垂径定理,垂径定理的推论,2垂直弦,4平分优弧,5平分劣弧,知二得三,火眼金睛,判断是非,在Rt△AOE中,又∵ACAB等内容,欢迎下载使用。













