初中数学人教版九年级上册23.1 图形的旋转课堂检测

这是一份初中数学人教版九年级上册23.1 图形的旋转课堂检测，共11页。试卷主要包含了1 图形的旋转等内容，欢迎下载使用。

23.1 图形的旋转


一．选择题


1．下列图片中，哪些是由图片（1）分别经过平移和旋转得到的（ ）





A．（3）和（4）B．（2）和（3）C．（2）和（4）D．（4）和（3）


2．下列事件中，属于旋转运动的是（ ）


A．小明向北走了4米B．时针转动


C．电梯从1楼到12楼D．一物体从高空坠下


3．下列图形中，绕某个点旋转72度后能与自身重合的是（ ）


A．B．C．D．


4．摩天轮上以等间隔的方式设置36个车厢，车厢依顺时针方向分别编号为1号到36号，且摩天轮运行时以逆时针方向等速旋转，旋转一圈花费30分钟．若图2表示21号车厢运行到最高点的情形，则此时经过多少分钟后，3号车厢才会运行到最高点？（ ）





A．14分钟B．20分钟C．15 分钟D．分钟


5．一个图形旋转后，下面结论中：①对应线段长度不变，②对应角相等，③位置不变，④各点旋转的角度相等．其中正确的个数是（ ）


A．1个B．2个C．3个D．4个


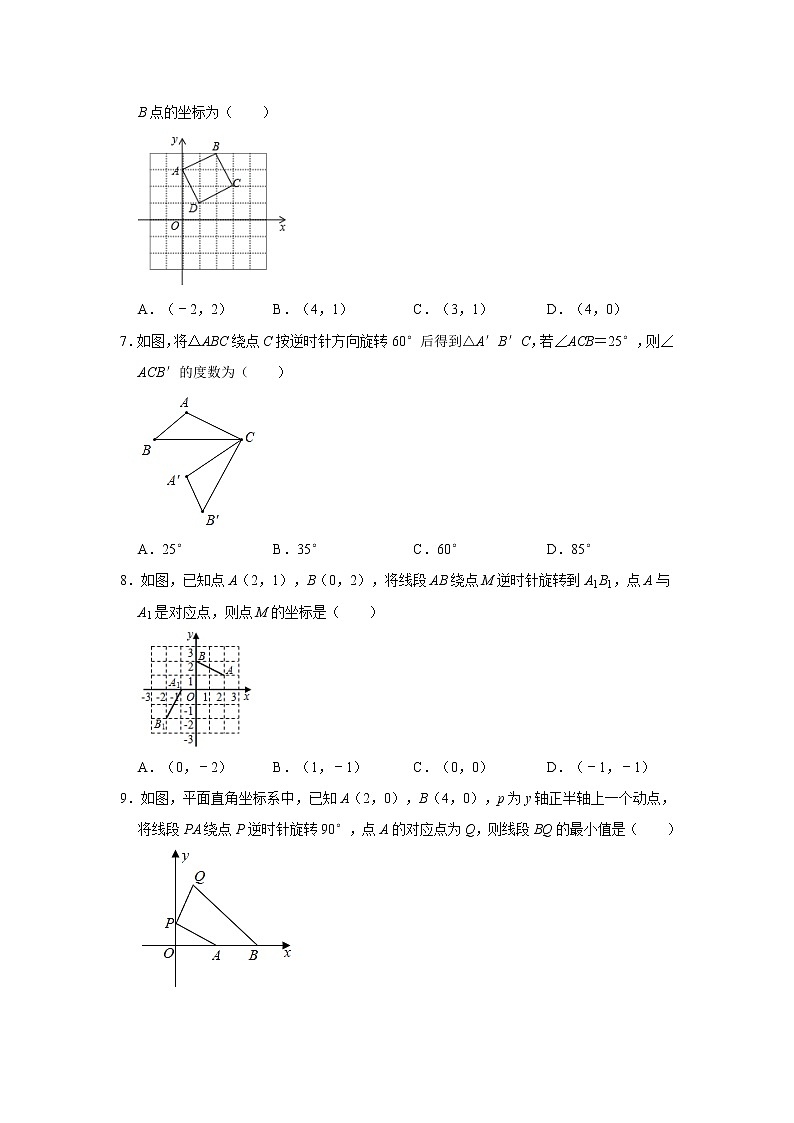
6．正方形ABCD在坐标系中的位置如图所示，将正方形ABCD绕D点顺时针旋转90°后，B点的坐标为（ ）





A．（﹣2，2）B．（4，1）C．（3，1）D．（4，0）


7．如图，将△ABC绕点C按逆时针方向旋转60°后得到△A′B′C，若∠ACB＝25°，则∠ACB′的度数为（ ）





A．25°B．35°C．60°D．85°


8．如图，已知点A（2，1），B（0，2），将线段AB绕点M逆时针旋转到A1B1，点A与A1是对应点，则点M的坐标是（ ）





A．（0，﹣2）B．（1，﹣1）C．（0，0）D．（﹣1，﹣1）


9．如图，平面直角坐标系中，已知A（2，0），B（4，0），p为y轴正半轴上一个动点，将线段PA绕点P逆时针旋转90°，点A的对应点为Q，则线段BQ的最小值是（ ）





A．3B．5C．D．2


二．填空题


10．如图，五角星也可以看作是一个三角形绕中心O旋转 次得到的，每次旋转角度是 ．





11．如图，风车图案围绕着旋转中心至少旋转 度，会和原图案重合．





12．如图，将△AOB绕点O按逆时针方向旋转50°后得到△COD，如果∠AOB＝15°，那么∠AOD的度数为 ．





13．如图，△A′BC′是△ABC绕点B顺时针旋转后得到的，则图中AB的对应线段是 ，∠A′BC′＝ ．





14．在平面直角坐标系中，已知点A的坐标为（2，3），点B的坐标为（1，0），点C是点A关于点B的对称点，则点C的坐标为 ．


15．如图，△ABO中BO＝AB＝6，AO＝5．在平面直角坐标系中将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处且点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…，则点C2000的坐标为 ．





三．解答题


16．如图，△AEC绕A点顺时针旋转60°得△APB，∠BAE＝20°，求∠PAC．








17．如图所示，把△ABC绕点A旋转至△ADE位置，延长BC交AD于F，交DE于G，若∠CAD＝10°，∠D＝25°，∠EAB＝120°，求∠DFB的度数．








18．如图在平面直角坐标系xOy中，A（6，0），B（6，6），将Rt△OAB绕点O逆时针旋转120°后得到Rt△OA1B1


（1）填空：∠A1OB＝ ；


（2）求A1的坐标；


（3）求B1的坐标．








19．如图，点E为正方形ABCD的边AB上一点，AB＝12，AE＝5，DE＝13，将△DAE旋转后能与△DCF重合．


（1）旋转中心是哪一点？


（2）旋转的最小角是多少度？


（3）求四边形DEBF的周长和面积．











20．如图，已知△ABC和△AEF中，∠B＝∠E，AB＝AE，BC＝EF，∠EAB＝25°，∠F＝57°；


（1）请说明∠EAB＝∠FAC的理由；


（2）△ABC可以经过图形的变换得到△AEF，请你描述这个变换；


（3）求∠AMB的度数．








参考答案


一．选择题


1．解：图（1）沿一直线平移可得到（3），顺时针旋转可得到（4）．


故选：A．


2．解：A．小明向北走了4米是平移，不合题意；


B．时针转动是旋转运动，符合题意；


C．电梯从1楼到12楼是平移，不合题意；


D．一物体从高空坠下是平移，不合题意；


故选：B．


3．解：A．旋转90°后能与自身重合，不合题意；


B．旋转72°后能与自身重合，符合题意；


C．旋转60°后能与自身重合，不合题意；


D．旋转45°后能与自身重合，不合题意；


故选：B．


4．解：（分钟）．


所以经过15分钟后，3号车厢才会运行到最高点．


故选：C．


5．解：①对应线段长度不变，说法正确；


②对应角相等，说法正确；


③位置不变，说法错误；


④各点旋转的角度相等，说法正确；


故选：C．


6．解：如图，正方形ABCD绕D点顺时针旋转90°得到正方形CB′C′D，即旋转后B点的坐标为（4，0）．





故选：D．


7．解：根据旋转的定义可知旋转角∠ACA′＝60°，


∵∠ACB＝25°，


∴∠A′CB′＝25°，


∴∠ACB′＝∠ACA′+∠A′CB′＝60°+25°＝85°．


故选：D．


8．解：如图，点M的坐标是（1，﹣1），


故选：B．





9．解：∵A（2，0），


∴OA＝2，


设P（0，m），则OP＝m，


作QM⊥y轴于M，


∵∠APQ＝90°，


∴∠OAP+∠APO＝∠APO+∠QPM，


∴∠OAP＝∠QPM，


∵∠AOP＝∠PMQ＝90°，PA＝PQ，


∴△AOP≌△PMQ（AAS），


∴MQ＝OP＝m，PM＝OA＝2，


∴Q（m，m+2），


∵B（4，0），


∴BQ＝＝，


∴当m＝1时，BQ有最小值3，


故选：A．





二．填空题


10．解：由于有五个星，所以要由一个三角形绕中心点旋转四次，


每次旋转的角度分别为等360°÷5＝72°，72°×2＝144°，72°×3＝216°，72°×4＝288°．


故答案为：四，72°，144°，216°，288°．


11．解：∵360°÷6＝60°，


∴该图形绕中心至少旋转60度后能和原来的图案互相重合．


故答案为：60．


12．解：由题意及旋转变换的性质得：


∠AOC＝∠BOD＝50°，


∵∠AOB＝15°，


∴∠AOD＝50°+15°＝65°，


故答案为：65°．


13．解：△A′BC′是△ABC绕点B顺时针旋转后得到的，则图中AB的对应线段是：A′B，


对应角∠A′BC′＝∠ABC．


故答案为：A′B，∠ABC．


14．解：设点C的坐标为（x，y），


∵点C是点A（2，3）关于点B（1，0）的对称点，


∴＝1，＝0，


解得x＝0，y＝﹣3，


∴点C的坐标为（0，﹣3）．


故答案为：（0，﹣3）．


15．解：由题意C2（17，0），C4（34，0），C6（51，0），…，C2n（17n，0），


∴C2000（17000，0），


故答案为（17000，0）．


三．解答题


16．解：根据旋转的性质可得△ABP≌△ACE，AC与AB是对应边，∠BAC＝∠BAE+∠EAC＝60°，


∵∠BAE＝20°，


∴∠EAC＝∠BAP＝40°，


∴∠PAC＝∠BAC+∠PAB＝100°．


17．解：由旋转可知：△ABC≌△ADE，


∵∠D＝25°，


∴∠B＝∠D＝25°，∠EAD＝∠CAB，


∵∠EAB＝∠EAD+∠CAD+∠CAB＝120°，∠CAD＝10°，


∴∠CAB＝（120°﹣10°）÷2＝55°，


∴∠FAB＝∠CAB+∠CAD＝55°+10°＝65°，


∵∠DFB是△ABF的外角，


∴∠DFB＝∠B+∠FAB，


∴∠DFB＝25°+65°＝90°．


18．解：（1）∵A（6，0），B（6，6），


∴△AOB是等腰直角三角形，


∴∠AOB＝45°，


∵∠AOA1＝120°，


∴∠A1OB＝75°，


故答案为75°．





（2）作A1H⊥y轴于H．


∵OA1＝6，∠A1OH＝30°，


∴A1H＝OA1＝3，OH＝A1H＝3，


∴A1（﹣3，3）．





（3）作B1K⊥OH于K，在B1K上取一点J，使得OJ＝JB1，连接OJ．


由题意OB1＝OB＝6，设OK＝m，则OJ＝JB＝2m，JK＝m，


∵OK2+B1K2＝B1O2，


∴m2+（2m+m）2＝72，


解得m＝3﹣3（负根已经舍弃），


∴KB1＝3+3，


∴B1（﹣3﹣3，3﹣3）．





19．解：（1）因为△DAE旋转后能与△DCF重合，所以旋转中心是点D；


（2）根据旋转的性质可知，△DAE≌△DCF，


∴∠EDF＝90°，


所以△DAE顺时针旋转270°后能与△DCF重合，△DAE逆时针旋转90°后能与△DCF重合，


即旋转的最小角是90°；


（3）∵∠EDF＝90°，DE＝DF，


∴△DEF是等腰直角三角形；


∵△DAE≌△DCF，


∴CF＝AE＝5，


∴BE+BF＝BE+BC+CF＝AB+BC＝12+12＝24，


∴四边形DEBF的周长＝BE+BF+DE+DF＝13+13+24＝50，


四边形DEBF的面积＝正方形ABCD的面积＝AD2＝144．


20．解：（1）∵∠B＝∠E，AB＝AE，BC＝EF，


∴△ABC≌△AEF，


∴∠C＝∠F，∠BAC＝∠EAF，


∴∠BAC﹣∠PAF＝∠EAF﹣∠PAF，


∴∠BAE＝∠CAF＝25°；





（2）通过观察可知△ABC绕点A顺时针旋转25°，可以得到△AEF；





（3）由（1）知∠C＝∠F＝57°，∠BAE＝∠CAF＝25°，


∴∠AMB＝∠C+∠CAF＝57°+25°＝82°．