人教版九年级上册第二十三章 旋转23.1 图形的旋转课时练习

这是一份人教版九年级上册第二十三章 旋转23.1 图形的旋转课时练习，共12页。试卷主要包含了1 图形的旋转同步练习卷，5°等内容，欢迎下载使用。

一．选择题


1．下列运动属于旋转的是（ ）


A．火箭升空的运动B．足球在草地上滚动


C．大风车运动的过程D．传输带运输的东西的运动


2．时间经过25分钟，钟表的分针旋转了（ ）


A．150°B．120°C．25°D．12.5°


3．下列现象中：①地下水位逐年下降；②传送带的移动；③方向盘的转动；④水龙头开关的转动；⑤钟摆的运动；⑥荡秋千运动．属于旋转的有（ ）


A．2个B．3个C．4个D．5个


4．一辆模型赛车，先前进1m，然后沿原地逆时针方向旋转，旋转角为α（0＜α＜90°），被称为一次操作，若五次操作后，发现赛车回到出发点，则旋转角α为（ ）


A．108°B．120°C．72°D．36°


5．如图，该图案绕它的中心至少旋转m度能与自身完全重合，则m的值是（ ）





A．45°B．90°C．135°D．180°


6．如图，在△ABC中，∠CAB＝∠ACB＝25°，将△ABC绕点A顺时针进行旋转，得到△AED．点C恰好在DE的延长线上，则∠EAC的度数为（ ）





A．75°B．90°C．105°D．120°


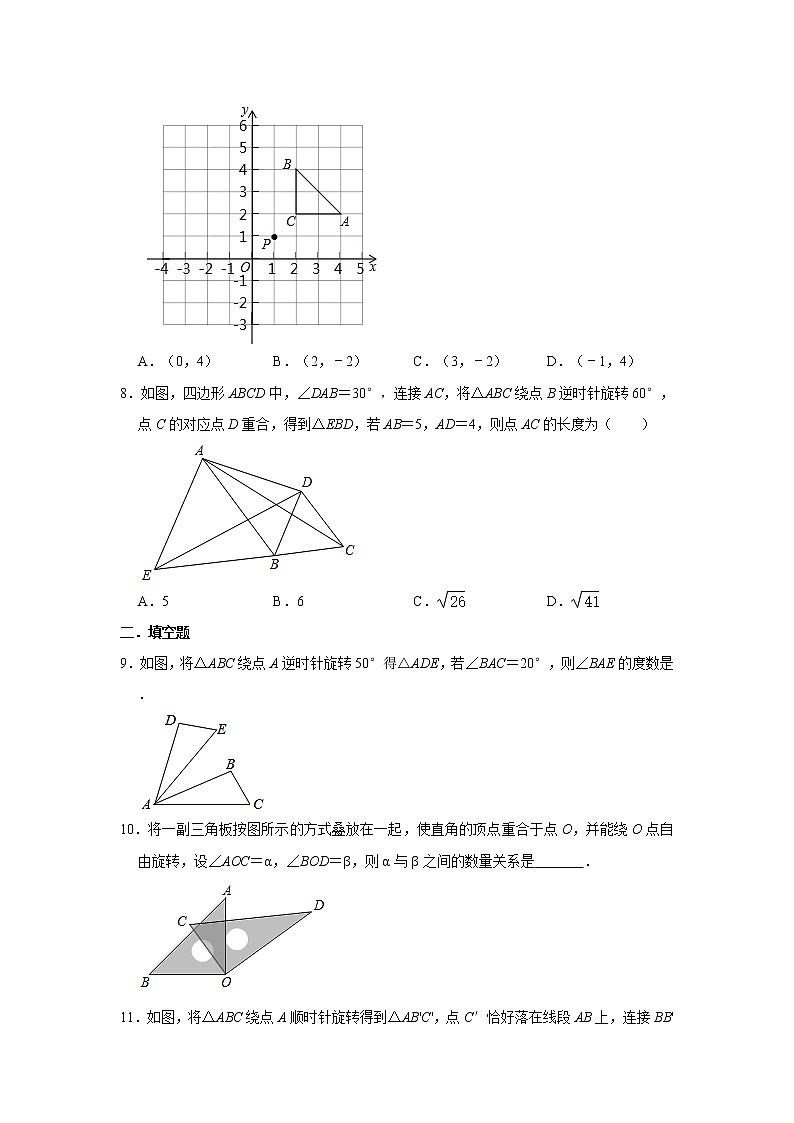
7．如图，将△ABC先向上平移1个单位，再绕点P按逆时针方向旋转90°，得到△A′B′C′，则点A的对应点A′的坐标是（ ）





A．（0，4）B．（2，﹣2）C．（3，﹣2）D．（﹣1，4）


8．如图，四边形ABCD中，∠DAB＝30°，连接AC，将△ABC绕点B逆时针旋转60°，点C的对应点D重合，得到△EBD，若AB＝5，AD＝4，则点AC的长度为（ ）





A．5B．6C．D．


二．填空题


9．如图，将△ABC绕点A逆时针旋转50°得△ADE，若∠BAC＝20°，则∠BAE的度数是 ．





10．将一副三角板按图所示的方式叠放在一起，使直角的顶点重合于点O，并能绕O点自由旋转，设∠AOC＝α，∠BOD＝β，则α与β之间的数量关系是 ．





11．如图，将△ABC绕点A顺时针旋转得到△AB'C'，点C′恰好落在线段AB上，连接BB'．若AC＝1，AB＝3，则BC′＝ ．





12．如图，在平面直角坐标系中，将点P（4，6）绕坐标原点O顺时针旋转90°得到点Q，则点Q的坐标为 ．





13．如图，△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕点B旋转得到△A'BC'，且点C的对应点C'刚好落在AB上，连接AA'．则∠AA'C'＝ ．





14．如图，在平面直角坐标系中，Rt△ABO直角点O在原点，AO在y轴上，BO在x轴上，且AO＝4，BO＝3，△ABO绕着各顶点向x轴正方向连续翻滚（始终保持一条边在x轴上）得到多个三角形，请问第2020个三角形的直角顶点坐标为 ．





三．解答题（共6小题）


15．如图，将△ABC绕点C顺时针旋转90°得到△EDC．若点A、D、E在同一条直线上，且∠ACB＝20°，求∠CAE及∠B的度数．





16．在△AMB中，∠AMB＝90°，AM＝8，BM＝6，将△AMB以B为旋转中心顺时针旋转90°得到△CNB．连接AC，求AC的长．





17．在正方形ABCD中，∠EDF＝45°，求证：EF＝AE+CF．





18．如图，△ABC是等边三角形，△ABP旋转后能与△CBP′重合．


（1）旋转中心是哪一点？


（2）旋转角度是多少度？


（3）连结PP′后，△BPP′是什么三角形？简单说明理由．





19．如图，△ABC逆时针旋转一定角度后与△ADE重合，且点C在AD上．


（1）指出旋转中心；


（2）若∠B＝21°，∠ACB＝26°，求出旋转的度数；


（3）若AB＝5，CD＝3，则AE的长是多少？为什么？





20．将两个全等的△ABC和△DBE按图1方式摆放，其中∠ACB＝∠DEB＝90°，∠A＝∠D＝30°，点E落在AB上，DE所在直线交AC所在直线于F．


（1）求证：AF+EF＝DE；


（2）若将图1中的△DBE绕点B顺时针旋转角a，且60°＜α＜180°，其他条件不变，如图2，请直接写出此时线段AF、EF与DE之间的数量关系．












































参考答案


一．选择题


1．解：A、火箭升空的运动，是平移，故此选项错误；


B、足球在草地上滚动，不是绕着某一个固定的点转动，不是旋转，故此选项错误；


C、大风车运动的过程，是旋转，故此选项正确；


D、传输带运输的东西的运动，是平移，故此选项错误；


故选：C．


2．解：如图所示：





因为分针每分钟转6°，所以25分钟旋转了6°×25＝150度．


故选：A．


3．解：①地下水位逐年下降，是平移现象；


②传送带的移动，是平移现象；


③方向盘的转动，是旋转现象；


④水龙头开关的转动，是旋转现象；


⑤钟摆的运动，是旋转现象；


⑥荡秋千运动，是旋转现象．


属于旋转的有③④⑤⑥共4个．


故选：C．


4．解：由题意，得赛车所走路线为正五边形，正五边形外角之和为360°，


所以五次旋转角之和为360°，


所以α＝360°÷5＝72°．


故选：C．


5．解：由题意这个图形是中心旋转图形，m＝＝45°，


故选：A．


6．解：∵将△ABC绕点A顺时针进行旋转，得到△AED，


∴△ABC≌△AED，


∴AD＝AC，∠BAC＝∠EAD＝25°，∠ADE＝∠ACB＝25°，


∴∠ADE＝∠ACD＝25°，


∴∠DAC＝180°﹣25°﹣25°＝130°，


∴∠EAC＝∠DAC﹣∠DAE＝130°﹣25°＝105°，


故选：C．


7．解：如图，





△A′B′C′即为所求，


则点A的对应点A′的坐标是（﹣1，4）．


故选：D．


8．解：∵△EBD是由△ABC旋转得到，


∴BA＝BE，∠ABE＝60°，AC＝DE，


∴△ABE是等边三角形，


∴∠EAB＝60°，


∵∠BAD＝30°，


∴∠EAD＝90°，


∵AE＝AB＝5，AD＝4，


∴DE＝＝＝，


故选：D．


二．填空题


9．解：由题意可得，


∠CAE＝50°，


∵∠BAC＝20°，


∴∠BAE＝∠CAE﹣∠BAC＝50°﹣20°＝30°，


故答案为：30°．


10．解：∵使直角的顶点重合于点O，并能绕O点自由旋转，


∴∠BOC＝∠AOD，


∵∠BOC+∠AOC＝90°，


∴∠AOD+∠AOC＝90°，


∵α+β＝∠AOC+∠BOD＝∠AOC+∠BOC+∠AOC+∠AOD＝180°，


∴α+β＝180°，


故答案为：α+β＝180°．


11．解：∵△ABC绕点A顺时针旋转得到△AB'C'，点C′恰好落在线段AB上，


∴AC′＝AC＝1，


∴BC′＝AB﹣AC′＝3﹣1＝2．


故答案为2．


12．解：作图如下，





∵∠MPO+∠POM＝90°，∠QON+∠POM＝90°，


∴∠MPO＝∠QON，


在△PMO和△ONQ中，


，


∴△PMO≌△ONQ（AAS），


∴PM＝ON，OM＝QN，


∵P点坐标为（4，6），


∴Q点坐标为（6，﹣4），


故答案为（6，﹣4）．


13．解：根据旋转可知：


∠A′BC＝∠ABC＝30°，A′B＝AB，


∴∠BA′A＝∠BAA′＝（180°﹣30°）＝75°，


∵∠BA′C＝∠BAC＝60°，


∴∠AA'C'＝∠BA′A﹣∠BA′C＝75°﹣60°＝15°．


故答案为：15°．


14．解：∵点A（0，4），B（3，0）


∴OA＝4，OB＝3


∴AB＝＝5，


∴三角形（3）的直角顶点坐标为：（12，0），


∵每3个三角形为一个循环组依次循环，


∵2020÷3＝673…1，


∴第2020个三角形是第674组的第一个直角三角形，其直角顶点与第673组的最后一个直角三角形顶点重合，


∵673×12＝8076，


∴第2020个三角形的直角顶点的坐标是（8076，0）．


故答案为（8076，0）．


三．解答题


15．解：根据旋转的性质可知CA＝CE，且∠ACE＝90°，


所以△ACE是等腰直角三角形．


所以∠CAE＝45°；


根据旋转的性质可得∠BDC＝90°，


∵∠ACB＝20°．


∴∠ACD＝90°﹣20°＝70°．


∴∠EDC＝45°+70°＝115°．


所以∠B＝∠EDC＝115°．


16．解：在Rt△AMB中，根据勾股定理可得


AB＝．


根据旋转的性质可知AB＝BC，∠ABC＝90°，


∴AC＝．


17．证明：∵四边形ABCD为正方形，


∴DA＝DC，∠A＝∠ADC＝90°，


把Rt△DAE绕点D逆时针旋转90°得到Rt△DCG，如图，


∴AE＝CG，DE＝DG，∠EDG＝90°，∠DCG＝∠A＝90°，


而∠DCF＝90°，


∴点G在BC的延长线上，


∴FG＝FC+CG，


∵∠EDF＝45°，


∴∠FDG＝∠EDG﹣∠EDF＝45°，


在△DFE和△DFG中，


，


∴△DFE≌△DFG（SAS），


∴EF＝FG，


∴EF＝FC+CG＝FC+AE．





18．解：（1）∵△ABP旋转后能与△P'BC重合，点B是对应点，没有改变，


∴点B是旋转中心；


（2）AB与BC是旋转前后对应边，


旋转角＝∠ABC，


∵△ABC是等边三角形，


∴∠ABC＝60°，


∴旋转角是60°；


（3）连结PP′后，△BPP′是等边三角形，


理由：∵旋转角是60°，


∴∠PBP′＝60°，


又∵BP＝BP′，


∴△BPP′是等边三角形．





19．解：（1）旋转中心为点A；





（2）∵∠B＝21°，∠ACB＝26°，


∴∠BAC＝180°﹣21°﹣26°＝133°，


∴旋转的度数为133°；





（3）由旋转性质知：AE＝AC，AD＝AB，


∴AE＝AB﹣CD＝2．


20．证明：（1）连接BF，





∵△ABC≌△DBE


∴BC＝BE，DE＝AC，AB＝BD，


∵BE＝BC，BF＝BF


∴Rt△BCF≌Rt△BEF（HL）


∴EF＝CF


∴DE＝AC＝AF+CF＝AF+EF


（2）连接BF，





∵△ABC≌△DBE


∴BC＝BE，DE＝AC，AB＝BD，


∵BE＝BC，BF＝BF


∴Rt△BCF≌Rt△BEF（HL）


∴EF＝CF


∴AF＝AC+CF＝DE+EF