数学人教版第十一章 三角形综合与测试同步测试题

这是一份数学人教版第十一章 三角形综合与测试同步测试题，共13页。试卷主要包含了有下列长度，如图所示，图中共有几个三角形，一个多边形切去一个角等内容，欢迎下载使用。




一．选择题


1．有下列长度（cm）的三条小木棒，如果首尾顺次连结，能钉成三角形的是（ ）


A．10、12、24B．12、16、32C．16、6、4D．8、10、12


2．如图所示，图中共有几个三角形（ ）





A．4B．6C．8D．10


3．如图，四边形ABCD中AD∥BC，∠A＝120°，DC⊥BC，BD平分∠ABC，则∠BDC＝（ ）





A．40°B．60°C．75°D．80°


4．下列各图中，CD属于△ABC的高的图形是（ ）


A．B．


C．D．


5．如图，利用所学的知识进行逻辑推理，工人盖房时常用木条EF固定矩形门框ABCD，使其不变形这种做法的根据是（ ）





A．两点之间线段最短B．矩形的对称性


C．矩形的四个角都是直角D．三角形的稳定性


6．如图，△ABC中，∠ABC＝∠ACB，∠A＝50°，P是△ABC内一点，且∠1＝∠2，则∠BPC等于（ ）





A．115°B．125°C．130°D．140°


7．如图，大五边形由若干个白色和灰色的多边形拼接而成，这些多边形（不包括大五边形）的所有内角和等于（ ）





A．4500°B．5000°C．5500°D．6000°


8．一个多边形切去一个角（即切去一个只含原多边形一个顶点的三角形）后，得到的新多边形的内角和与原多边形内角和相比（ ）


A．多180°B．少180°C．多360°D．相等


9．我们知道三角形的内角和为180°，而四边形可以分成两个三角形，故它的内角和为2×180°＝360°，五边形则可以分成3个三角形，它的内角和为3×180°＝540°（如图），依此类推，则八边形的内角和为（ ）





A．900°B．1080°C．1260°D．1440°


10．如图，△ABC，∠ABC、∠ACB的三等分线交于点E、D，若∠BFC＝132°，∠BGC＝118°，则∠A的度数为（ ）





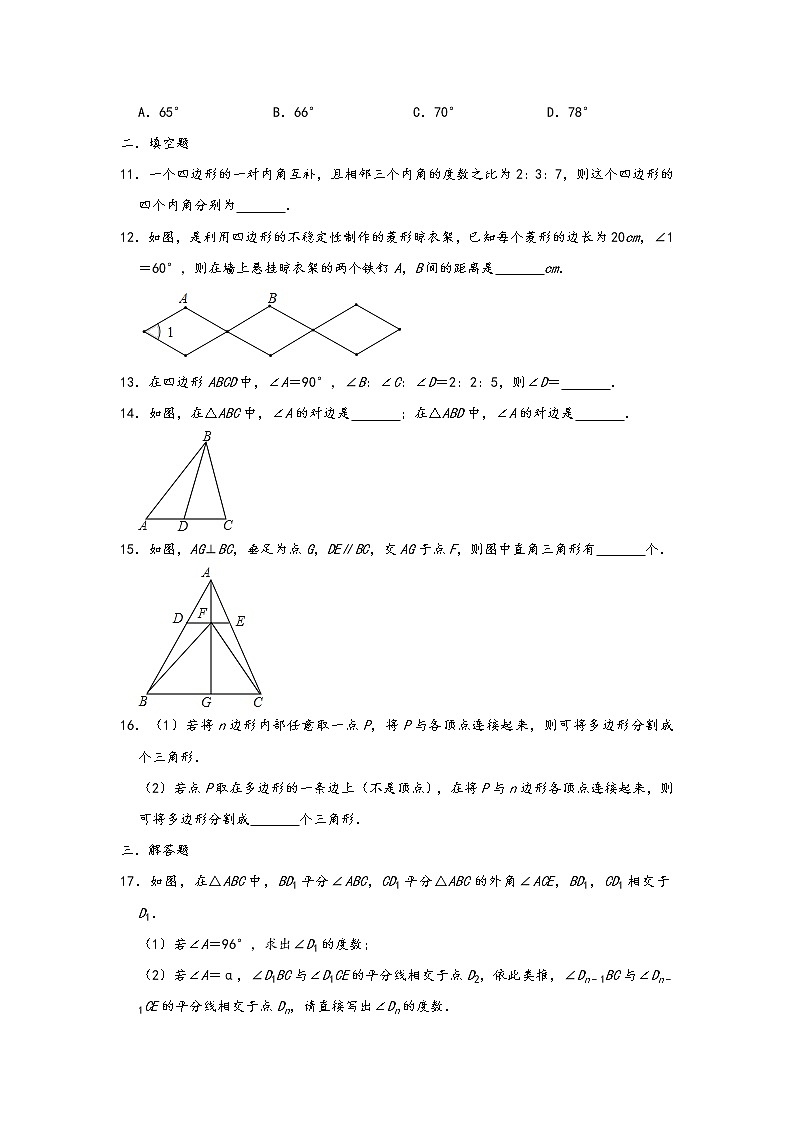
A．65°B．66°C．70°D．78°


二．填空题


11．一个四边形的一对内角互补，且相邻三个内角的度数之比为2：3：7，则这个四边形的四个内角分别为 ．


12．如图，是利用四边形的不稳定性制作的菱形晾衣架，已知每个菱形的边长为20cm，∠1＝60°，则在墙上悬挂晾衣架的两个铁钉A，B间的距离是 cm．





13．在四边形ABCD中，∠A＝90°，∠B：∠C：∠D＝2：2：5，则∠D＝ ．


14．如图，在△ABC中，∠A的对边是 ；在△ABD中，∠A的对边是 ．





15．如图，AG⊥BC，垂足为点G，DE∥BC，交AG于点F，则图中直角三角形有 个．





16．（1）若将n边形内部任意取一点P，将P与各顶点连接起来，则可将多边形分割成 个三角形．


（2）若点P取在多边形的一条边上（不是顶点），在将P与n边形各顶点连接起来，则可将多边形分割成 个三角形．


三．解答题


17．如图，在△ABC中，BD1平分∠ABC，CD1平分△ABC的外角∠ACE，BD1，CD1相交于D1．


（1）若∠A＝96°，求出∠D1的度数；


（2）若∠A＝α，∠D1BC与∠D1CE的平分线相交于点D2，依此类推，∠Dn﹣1BC与∠Dn﹣1CE的平分线相交于点Dn，请直接写出∠Dn的度数．





18．用几何画板工具可以很方便地画出正五角星（如图1所示）．


（1）图1中∠CAD+∠B+∠C+∠D+∠E＝ ；


（2）拖动点A到图2和图3的位置时，∠CAD+∠B+∠C+∠D+∠E的值是否发生变化？说明你的理由．


19．先看下面的问题：图（1）中，BE∥AC，则∠1＝∠C，∠2＝∠A，因为∠ABC+∠1+∠2＝180°．（平角定义），所以得∠ABC+∠C+∠A＝180°．





（1）你能结合图（2）得到类似的结论吗？请你写出来（其中CD∥AB且过点C）；


（2）你能写出一个与三角形有关的具有一般性的结论吗？联系上面的问题试试看！


20．（探索题）如图△ABC中，∠ABC，∠ACB的平分线相交于点O．


（1）若∠ABC＝40°，∠ACB＝80°，求∠BOC；


（2）你能找出∠A与∠BOC之间的数量关系吗？





21．如图1、图2、图3中，点E、D分别是正△ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点的一边延长线和另一边反向延长线上的点，且△ABE与△BCD能互相重合，BD延长线交AE于点F．


（1）求图1中，∠AFB的度数；


（2）图2中，∠AFB的度数为 ，图3中，∠AFB的度数为 ．





22．（1）如图所示，在△ABC中，AD丄BC于D，AE平分∠BAC，且∠C大于∠B，求证：∠EAD＝（∠C﹣∠B）．


（2）若把问题（1）中的“AD丄BC”改为“点F为EA上一点且FD丄BC于D”，画出新的图形，并试说明∠EFD＝（∠C﹣∠B）．


（3）若把问题（2）中的“F为EA上一点”改为“F为AE延长线上的一点”，则问题（2）中的结论成立吗？请说明你的理由．





23．如图1，已知线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”．如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试解答下列问题：


（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系： ；


（2）仔细观察，在图2中“8字形”的个数： 个；


（3）在图2中，若∠D＝40°，∠P＝30°，试求∠B的度数；


（4）如果图2中∠D和∠B为任意角时，其他条件不变，试写出∠B与∠P、∠D之间数量关系．并说明理由．








参考答案


一．选择题


1．解：A、10+12＜24，不满足三角形三边关系定理，故错误；


B、12+16＝28．不满足三角形三边关系定理，故错误；


C、6+4＜16．不满足三边关系定理，故错误；


D、8+10＞12．满足三边关系定理，故正确．


故选：D．


2．解：4+4＝8（个）．


故选：C．


3．解：∵AD∥BC，


∴∠A+∠ABC＝180°，


∵∠A＝120°，


∴∠ABC＝180°﹣120°＝60°，


∵BD平分∠ABC，


∴∠DBC＝30°．


∵DC⊥BC，


∴∠C＝90°，


∴∠BDC＝180°﹣∠DBC﹣∠C＝60°．


故选：B．


4．解：AB边上的高就是过C作垂线垂直AB交AB于某点，因此只有A符合条件，


故选：A．


5．解：工人盖房时常用木条EF固定矩形门框ABCD，使其不变形这种做法的根据是三角形的稳定性，


故选：D．


6．解：∵∠A＝50°，


∴∠ACB+∠ABC＝180°﹣50°＝130°，


又∵∠ABC＝∠ACB，∠1＝∠2，


∴∠PBA＝∠PCB，


∴∠1+∠ABP＝∠PCB+∠2＝130°×＝65°，


∴∠BPC＝180°﹣65°＝115°．


故选：A．


7．解：结合图形，得


这些多边形（不包括大五边形）的所有内角和等于5×180°+10×360°＝4500°．


故选：A．


8．解：得到的新多边形的内角和与原多边形内角和相比多180度．


故选：A．


9．解：6×180°＝1080度．故选B．


10．解：


∵∠ABC、∠ACB的三等分线交于点E、D，


∴∠FBC＝2∠DBC，∠GCB＝2∠DCB，


∵∠BFC＝132°，∠BGC＝118°，


∴∠FBC+∠DCB＝180°﹣∠BFC＝180°﹣132°＝48°，


∠DBC+∠GCB＝180°﹣∠BGC＝180°﹣118°＝62°，


即，


由①+②可得：3（∠DBC+∠DCB）＝110°，


∴∠ABC+∠ACB＝3（∠DBC+∠DCB）＝110°，


∴∠A＝180°﹣（∠ABC+∠ACB）＝180°﹣110°＝70°，


故选：C．


二．填空题（共6小题）


11．解：∵四边形的一对内角互补，且相邻三个内角的度数之比为2：3：7，


∴这个四边形的四个内角的度数之比为2：3：7：6或2：3：7：8，


∴这个四边形的四个内角分别为，，，或，，，．


故答案为：40°，60°，140°，120°或36°，54°，126°，144°．


12．解：如图：





∵在一个菱形中，∠1＝60°，


∴△ACD是等边三角形，∠APD＝90°，∠ADP＝30°，


∴AC＝AD＝20cm，＝10（cm），


∴DE＝2DP＝＝＝（cm），


∵AB＝DE，


∴两个铁钉A、B之间的距离是20cm．


故答案为：．


13．解：∵四边形ABCD的内角和为（4﹣2）×180°＝360°，


∴∠B+∠C+∠D＝360°﹣∠A＝270°，


又∵∠B：∠C：∠D＝2：2：5


∴∠D＝＝150°．


故答案为：150°．


14．解：在△ABC中，∠A的对边是BC；


在△ABD中，∠A的对边是BD；


故答案为：BC；BD．


15．解：∵AG⊥BG，∴∠AGB＝∠AGC＝90°，


∴△ABG，△ACG，△BFG，△CFG是直角三角形，


∵DE∥BC，


∴∠AFD＝∠AGB＝90°，∠AFE＝∠AGC＝90°，


∴△AFD，△AFE是直角三角形，


所以直角三角形有：△ABG，△ACG，△BFG，△CFG，△AFD，△AFE共6个．


故应填6．


16．解：（1）若将n边形内部任意取一点P，将P与各顶点连接起来，则可将多边形分割成n个三角形；





（2）若点P取在多边形的一条边上（不是顶点），在将P与n边形各顶点连接起来，则可将多边形分割成（n﹣1）个三角形．


故答案为：n，（n﹣1）．


三．解答题（共7小题）


17．解：（1）∵BD平分∠ABC，CD1平分∠ACE，


∴∠ABC＝2∠D1BC，∠ACE＝2∠D1CE，


∵∠ACE＝2∠D1CE＝∠A+∠ABC，∠D1CE＝∠D1+∠D1BC，


∴2∠D1CE＝2∠D1+2∠D1BC，


∴∠ACE＝2∠D1+∠ABC，


∴2∠D1+∠ABC＝∠A+∠ABC，


∴∠A＝2∠D1，


∵∠A＝96°，


∴∠D1＝∠A＝48°；





（2）由（1）的结论可知，∠D1＝∠A，


同理可得，∠D2＝∠A，


故∠Dn＝∠A．


18．解：（1）设BD，CE交于M；AD，CE交于N，


则∠A+∠C＝∠ANE＝∠MND，


∠B+∠E＝∠CMB＝∠DMN，


而∠MND+∠DMN+∠D＝180，


所以∠A+∠B+∠C+∠D+∠E＝180°；





（2）∠CAD+∠B+∠C+∠D+∠E值没有变化．


证明：设BD，CE交于M；AD，CE交于N，


则∠A+∠C＝∠ANE＝∠MND，


∠B+∠E＝∠CMB＝∠DMN，


而∠MND+∠DMN+∠D＝180，


所以∠A+∠B+∠C+∠D+∠E＝180°．





19．解：（1）∵CD∥AB，


∴∠A+∠ACD＝180°，（两直线平行，同旁内角互补）


∠2＝∠B，（两直线平行，内错角相等）


又∵∠ACD＝∠ACB+∠2，


∴∠ACD＝∠ACB+∠B，


∴∠A+∠B+∠ACB＝180°．





（2）三角形的三个内角的和等于180°．


20．解：（1）∠BOC＝180°﹣∠OBC﹣∠OCB


＝180°﹣（∠OBC+∠OCB）


＝180°﹣（40°+80°）


＝180°﹣×120°


＝120°；





（2）∠BOC＝180°﹣（∠ABC+∠ACB）


＝180°﹣（180°﹣∠A）


＝90°+∠A．


21．解：（1）∵△ABE与△BCD能互相重合，


∴∠D＝∠E，


∵∠DBC＝∠EBF，


∴∠BFE＝180°﹣∠E﹣∠EBF＝180°﹣∠D﹣∠B＝∠BCD．


∵∠BCD+∠ACB＝180°，∠ACB＝60°，∠AFB+∠BFE＝180°，


∴∠AFB＝∠ACB＝60°．


（2）同理可得出：∠AFB＝∠BCM，


∵四边形ABCD为正方形，五边形ABCMN为正五边形，


∴图2中∠BCM＝90°，图3中∠BCM＝108°．


故答案为：90°；108°．


22．（1）证明：在Rt△ADE中，


∵∠AED+∠DAE＝90°，


∴∠DAE＝90°﹣∠AED，


∵∠AED＝∠AEC＝180°﹣∠C﹣∠CAE，且AE平分∠BAC，


∴∠CAE＝∠BAC＝（180°﹣∠C﹣∠B），


∴∠DAE＝90°﹣[180°﹣∠C﹣（180°﹣∠C﹣∠B）]＝（∠C﹣∠B）．





（2）由三角形的外角性质知：∠FED＝∠AEC＝∠B+∠BAC，


故∠B+∠BAC+∠EFD＝90°；①


在△ABC中，由三角形内角和定理得：∠B+∠BAC+∠C＝180°，


即：∠C+∠B+∠BAC═90°，②


②﹣①，得：∠EFD＝（∠C﹣∠B）．





（3）由三角形的外角性质知：∠FED＝∠AEC＝∠B+∠BAC，


故∠B+∠BAC+∠EFD＝90°；①


在△ABC中，由三角形内角和定理得：∠B+∠BAC+∠C＝180°，


即：∠C+∠B+∠BAC═90°，②


②﹣①，得：∠EFD＝（∠C﹣∠B）．





23．解：（1）∵∠A+∠D+∠AOD＝180°，∠C+∠D+∠BOC＝180°，


而∠AOD＝∠BOC，


∴∠A+∠D＝∠B+∠C；


故答案为∠A+∠D＝∠B+∠C；


（2）以M为交点的“8字形”有1个，以N为交点的“8字形”有1个，以O为交点的“8字形”有4个，共6个；


故答案为6；





（3）∵∠DAB和∠BCD的平分线AP和CP相交于点P，


∴∠1＝∠2，∠3＝∠4，


∵∠1+∠D＝∠3+∠P，∠2+∠P＝∠4+∠B，


∴∠D﹣∠P＝∠P﹣∠B，


即∠P＝（∠D+∠B），


∵∠D＝40°，∠P＝30°


∴∠B＝60﹣40＝20°


（4）由（3）可知：∠P＝（∠B+∠D）．