初中数学人教版九年级下册第二十七章 相似综合与测试课文内容ppt课件

这是一份初中数学人教版九年级下册第二十七章 相似综合与测试课文内容ppt课件，共21页。

一、“A”字型【例1】如图，△ABC是边长为3的等边三角形，点E，F分别在AC，BC边上，连接AF，BE相交于点P，∠APE＝60°.
(1)求证：△APE∽△ACF；(2)若AE＝1，求AP·AF的值．分析：(1)由△ABC是等边三角形得到∠C＝60°，从而可由两角相等判定三角形相似；
[对应训练]1．如图，在△ABC中，BE平分∠ABC交AC于点E，过点E作ED∥BC交AB于点D.(1)求证：AE·BC＝BD·AC；(2)如果S△ADE＝3，S△BDE＝2，DE＝6，求BC的长．
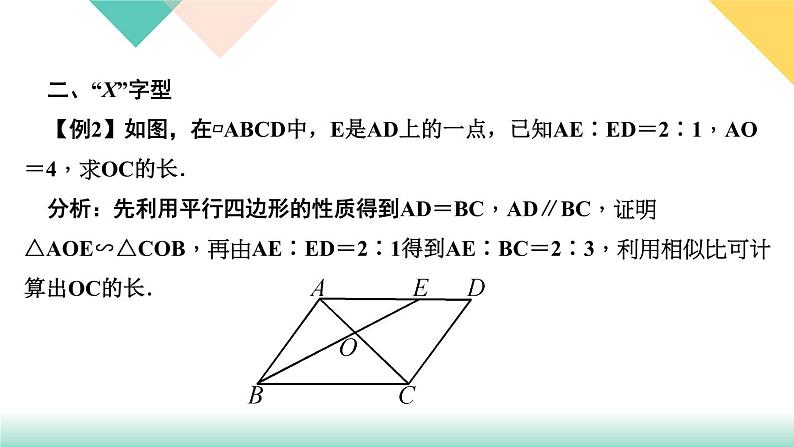
二、“X”字型【例2】如图，在▱ABCD中，E是AD上的一点，已知AE∶ED＝2∶1，AO＝4，求OC的长．分析：先利用平行四边形的性质得到AD＝BC，AD∥BC，证明△AOE∽△COB，再由AE∶ED＝2∶1得到AE∶BC＝2∶3，利用相似比可计算出OC的长．
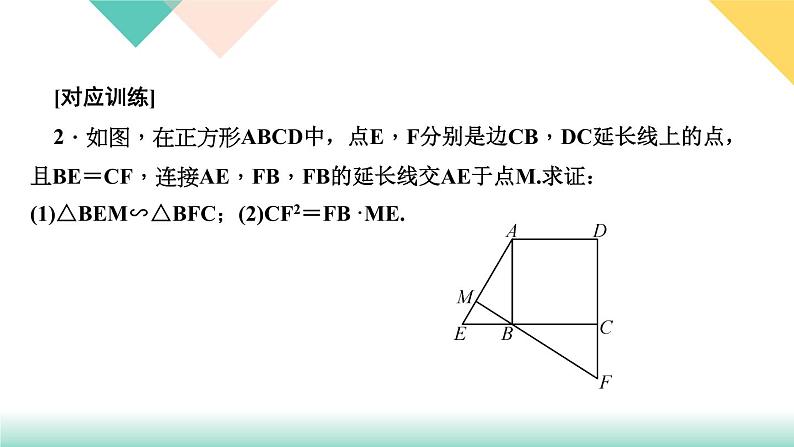
[对应训练]2．如图，在正方形ABCD中，点E，F分别是边CB，DC延长线上的点，且BE＝CF，连接AE，FB，FB的延长线交AE于点M.求证：(1)△BEM∽△BFC；(2)CF2＝FB·ME.
三、旋转型【例3】如图，＝＝，B，D，F，E在同一条直线上，请找出图中的相似三角形，并说明理由．分析：根据三边成比例的两个三角形相似，即可证得△ABC∽△ADE，可得∠BAD＝∠CAE，又由两边成比例且夹角相等的两个三角形相似，即可证得△BAD∽△CAE，可得∠ABD＝∠ACE.由∠ACB＝∠AED，∠AFE＝∠BFC，可证得△AFE∽△BFC.由∠AFB＝∠EFC，∠ABF＝∠ECF，可证得△ABF∽△ECF.
[对应训练]3．如图，在△ABC和△AED中，AB·AD＝AC·AE，∠CAE＝∠BAD，S△ADE＝4S△ABC.求证：DE＝2BC.
[对应训练]4．如图，在矩形ABCD中，AB＝6，AD＝12，点E在边AD上，且AE＝8，EF⊥BE交CD于点F.(1)求证：△ABE∽△DEF；(2)求EF的长．