人教版数学九年级下册 27.4.2第13讲《相似三角形的性质与判定》专项复习 课件+教案+分层练习+预习案

人教版数学九年级下册

27.4.2第13讲 相似三角形的性质与判定 分层练习

【基础篇】

测试题1  如图，平行四边形ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF:FC等于（    ）

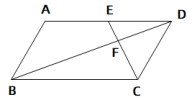
A. 3：2       B. 3：1        C. 1：1        D. 1：2

答案：D

因为是平行四边形中边的中点，所以，所以，故选D.故选：A．

测试题2  如图，在△ABC中，点D、E分别是边AB、AC的中点，BE与CD相交于点G，则DG：GC的值为（    ）

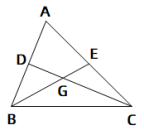
A. 3 ：4      B. 2 ：3        C. 1 ：2         D. 1 ：3

答案：C

测试题3  如图，在△ABC中，若∠AED＝∠B，DE＝6，AB＝10，AE＝8，则BC的长为（ 　）

A.         B.7           C.           D.

答案：C

解析过程：∵∠AED＝∠B，∠A＝∠A

∴△ADE∽△ACB

∴

∵DE＝6，AB＝10，AE＝8

∴，解得

故选C.

测试题4  如图，在△ABC中，∠ACB=90°，CD⊥AB于点D，下列说法中正确的个数是（　　）

①AC·BC=AB·CD

②AC2=AD·DB

③BC2=BD·BA

④CD2=AD·DB．

A. 1个       B. 2个         C. 3个         D. 4个

答案：C

解析过程：∵在△ABC中，∠ACB=90°，CD⊥AB，

∴∠BDC=∠BCA=∠CDA=90°，

∵∠A=∠A，∠B=∠B，

∴△ACD∽△ABC，△BDC∽△BCA，

∴AC·AB=BC·CD，故①正确；

BC2=BD·BA，故③正确；

∴△ACD∽△CBD，

∴AC2=AD·AB，CD2=AD·DB，

故②错误，

④正确．

下列说法中正确的个数是3个．

故选C．

【能力篇】

测试题5  如图，在△ABC中，D是AB上一点，且∠ACD=∠B，已知AD=8cm，BD=4cm，求AC的长．

解析过程：∵在△ACD和△ABC中，

，

∴△ACD∽△ABC，

∴=，

∵AD=8cm，BD=4cm，

∴AB=12cm，

∴=，

∴AC=cm．

【拔高篇】

6．从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．

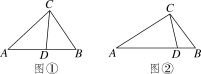
(1)如图①，在△ABC中，CD为角平分线，∠A＝40°，∠B＝60°，求证：CD为△ABC的完美分割线；

(2)在△ABC中，∠A＝48°，CD是△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数；

(3)如图②，△ABC中，AC＝2，BC＝，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长．

6．解：(1)如图①中，∵∠A＝40°，∠B＝60°，∴∠ACB＝80°，

∴△ABC不是等腰三角形．

∵CD平分∠ACB，∴∠ACD＝∠BCD＝∠ACB＝40°，

∴∠ACD＝∠A＝40°，∴△ACD为等腰三角形．

∵∠DCB＝∠A＝40°，∠CBD＝∠ABC，∴△BCD∽△BAC，

∴CD是△ABC的完美分割线；

(2)①当AD＝CD时，如图②，∠ACD＝∠A＝48°，∵△BDC∽△BCA，∴∠BCD＝∠A＝48°，∴∠ACB＝∠ACD＋∠BCD＝96°；

②当AD＝AC时，如图③，∠ACD＝∠ADC＝＝66°.∵△BDC∽△BCA，∴∠BCD＝∠A＝48°，∴∠ACB＝∠ACD＋∠BCD＝114°；

③当AC＝CD时，如图④中，∠ADC＝∠A＝48°，∵△BDC∽△BCA，∴∠BCD＝∠A＝48°.∵∠ADC>∠BCD，矛盾，舍弃．∴∠ACB＝96°或114°；

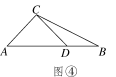
(3)由已知AC＝AD＝2，

∵△BCD∽△BAC，∴＝，设BD＝x，

∴()2＝x(x＋2)．

∵x>0，∴x＝－1.

∵△BCD∽△BAC，∴＝＝，

∴CD＝×2＝－.