人教版数学九年级下册 第二十七章 《相似》（章末小结）课件+章末测试（含答案解析）

这是一份人教版数学九年级下册 第二十七章 《相似》（章末小结）课件+章末测试（含答案解析），共53页。

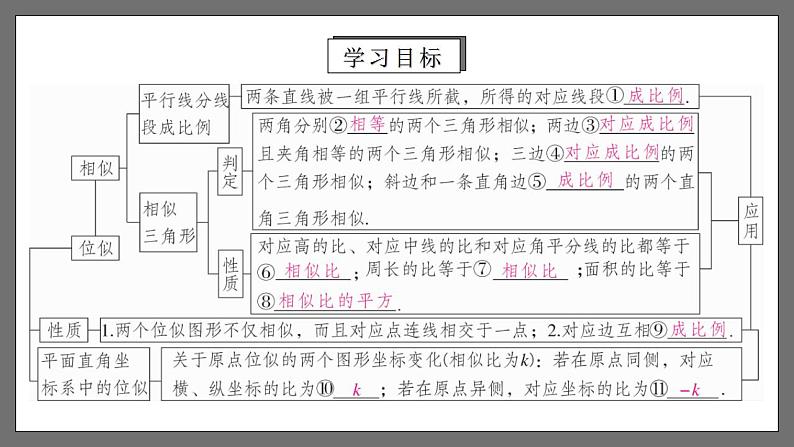
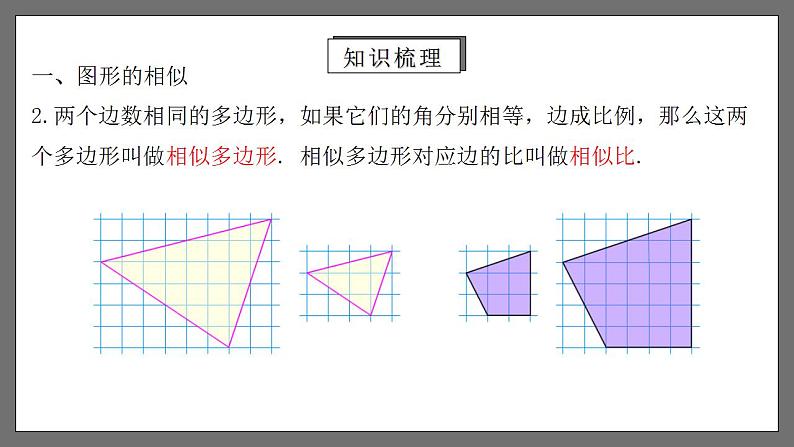
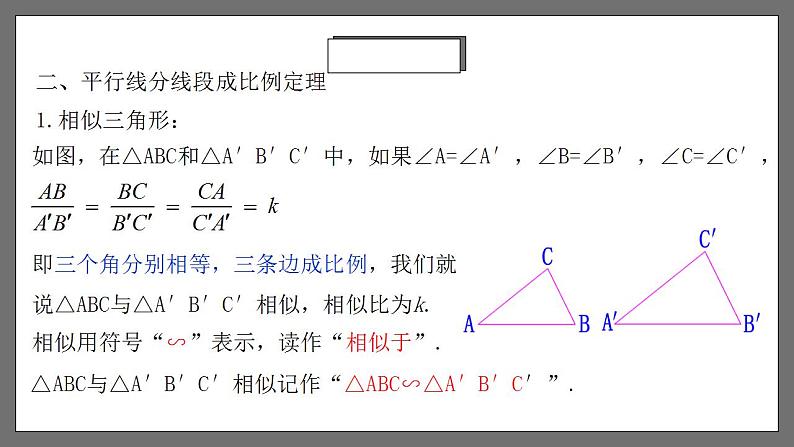
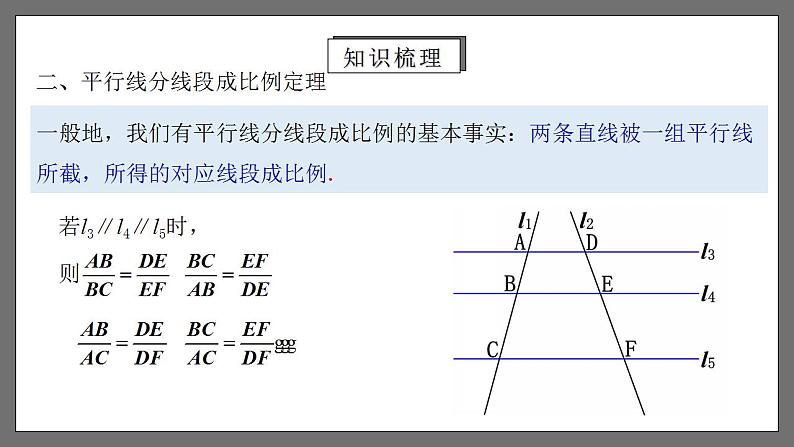
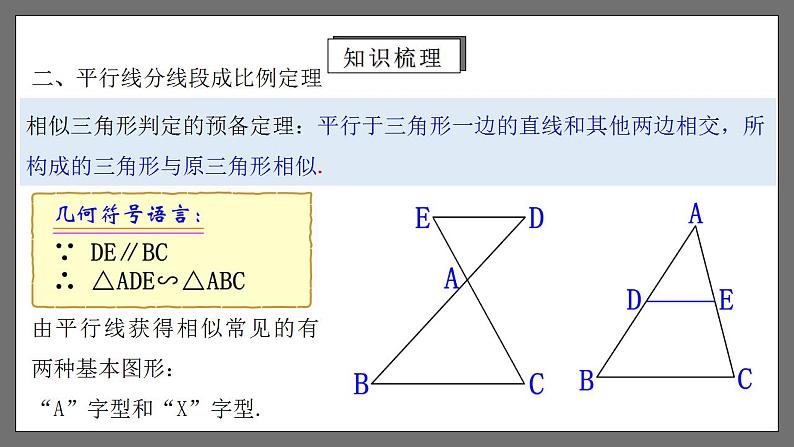
相似 章末小结1.疏通本章知识,弄清知识脉络.2.进一步熟悉相似三角形的判定及其性质，并能运用这些判定和性质解决一些相应的问题.(重点、 难点)3.知道什么是位似，能利用位似将一个图形放大或缩小，知道位似变换的点的坐标变化规律.学习目标学习目标一、图形的相似1.我们把__________的图形叫做__________.相似图形形状相同两个图形相似，其中一个图形可以看作由另一个图形放大或缩小得到.(1)相似图形的本质特征是形状相同，与大小，位置等因素无关.(2)全等图形可以看成是一种特殊的相似，即不仅形状相同，而且大小也相同.知识梳理一、图形的相似2.两个边数相同的多边形，如果它们的角分别相等，边成比例，那么这两个多边形叫做相似多边形. 相似多边形对应边的比叫做相似比.知识梳理二、平行线分线段成比例定理如图，在△ABC和△A′B′C′中，如果∠A=∠A′，∠B=∠B′，∠C=∠C′，即三个角分别相等，三条边成比例，我们就说△ABC与△A′B′C′相似，相似比为k.相似用符号“∽”表示，读作“相似于”. △ABC与△A′B′C′相似记作“△ABC∽△A′B′C′”.1.相似三角形：二、平行线分线段成比例定理一般地，我们有平行线分线段成比例的基本事实：两条直线被一组平行线所截，所得的对应线段成比例.知识梳理相似三角形判定的预备定理：平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似.由平行线获得相似常见的有两种基本图形：“A”字型和“X”字型.二、平行线分线段成比例定理知识梳理利用三边判定两个三角形相似的定理1：三边成比例的两个三角形相似.三、相似三角形的判定知识梳理利用两边和夹角判定两个三角形相似的定理2：两边成比例且夹角相等的两个三角形相似.三、相似三角形的判定知识梳理三、相似三角形的判定利用两组角判定两个三角形相似的定理3：两角分别相等的两个三角形相似.知识梳理三、相似三角形的判定判定直角三角形相似的方法：斜边和一直角边成比例的两个直角三角形相似.知识梳理四、相似三角形的性质1.相似三角形对应线段之比相似三角形对应高的比，对应中线的比与对应角平分线的比都等于相似比.2.相似三角形的周长之比相似三角形周长的比等于相似比.类似地，相似多边形周长的比等于相似比.3.相似三角形的面积之比相似三角形面积的比等于相似比的平方.类似地，相似多边形面积的比等于相似比的平方.知识梳理五、相似三角形的应用表达式：物1高 ：物2高 = 影1长 ：影2长测量不能到达顶部的物体的高度，可以用“在同一时刻物高与影长成正比例”的原理解决.1.利用相似三角形测量高度知识梳理测量如河宽等不易直接测量的物体的宽度，常构造相似三角形求解. 2.利用相似三角形测量河宽五、相似三角形的应用知识梳理1.图中，每幅图的两个多边形不仅相似，而且对应顶点的连线相交于一点，像这样的两个图形叫做位似图形，这点叫做位似中心.这时我们说这两个图形关于这点位似.这时的相似比又称位似比.六、位似知识梳理2.利用位似，可以将一个图形放大或缩小，主要方法有两种：  方法一：在图形外取一点作为位似中心，按要求将图形放大或缩小；  方法二：在图形内取一点作为位似中心，按要求将图形放大或缩小.  六、位似知识梳理3.利用位似作图形的基本过程：(1)确定位似中心；(2)连接图形各顶点与位似中心；(3)在连接图形各顶点与位似中心的线段或其延长线(或反向延长线)上按位似比进行取点；(4)顺次连接各点，所得图形就是所要求的图形.六、位似知识梳理一般地，在平面直角坐标系中，如果以原点为位似中心，画出一个与原图形位似的图形，使它与原图形的相似比为k，那么与原图形上的点(x，y)对应的位似图形上的点的坐标为(___，___)或(____，____).kxky-kx-ky六、位似知识梳理考点梳理例1.已知有三条长度分别为2cm、4cm、8cm的线段，请再添一条线段．使这四条线段成比例，求所添线段的长度． 考点解析  考点解析 BAB迁移应用  C考点解析  考点解析  C考点解析【2-1】如图，直线l1//l2//l3， 直线AC分别与直线l1, l2, l3交于A、B、C三点，直线DF分别与直线l1，l2,l3交于D、E、F三点，AC与DF交于点O.若BC=2AO=2OB， OD=1， 则OF的长是( )A.1 B.2 C.3 D.4C迁移应用【2-2】如图，在平行四边形ABCD中,E是边BC上的一点，且BE:EC=3:2,连接AE、BD交于点F，则BF:FD=_______.3：5迁移应用  迁移应用  迁移应用   考点解析  考点解析  考点解析【3-1】如图，已知矩形ABCD的顶点A、D分别落在x轴、y轴上,OD=2OA=6， AD:AB=3:1， 则点C的坐标为_________.(2，7)迁移应用【3-2】如图，已知△ABC，P是边AB上的一点，连接CP，以下条件中不能判定△ACP∽△ABC的是( )A.∠ACP=∠B B.∠APC=∠ACB C. AC2=AP·AB D.AC·BC=AB·CPD迁移应用【3-3】如图，在边长为4的正方形ABCD中，P是BC上的点，且BP＝3PC，Q是CD的中点，求证：△ADQ∽△QCP． 迁移应用例7.△ABC中，DE∥BC，EF∥AB，已知△ADE 和△EFC的面积分别为4和9，求△ABC的面积.解：∵ DE∥BC，EF∥AB∴△ADE∽△ABC,∠AED=∠C，∠A=∠CEF∴△ADE∽△EFC又∵S△ADE:S△EFC =4:9∴AE:EC=2:3则AE:AC=2:5∴ S△ADE:S△ABC =4:25∴ S△ABC =25考点解析 A C迁移应用 B迁移应用例8.如图，某一时刻一根2m长的竹竿EF的影长GE为1.2m，此时，小红测得一棵被风吹斜的柏树与地面成30°角，树顶端B在地面上的影子点D与B到垂直地面的落点C的距离是3.6m，求树AB的长．解：如图，CD＝3.6m，∵△BDC∽△FGE，∴ BC＝6m.在Rt△ABC中，∵ ∠A＝30°，∴ AB＝2BC＝12m，即树长AB是12m.考点解析例9.教学楼旁边有一棵树，课外数学兴趣小组在阳光下，测得一根长为1m的竹竿的影长为0.9m,但他们马上测树的影长时，发现树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上，如图所示.经过一番争论，该小组的同学认为继续测量也可以求出树高，他们测得落在地面.上的影长为2.7m，落在墙璧上影长为1.2m，请你和他们一起计算一下， 树高为多少?考点解析解:根据题意，画出示意图，延长AD、BE相交于C,则CE是无墙壁遮挡时树影长的一部分.∴ ,即∴CE=1.08(m)∴BC=BE+CE=2.7+1.08=3.78(m)又∵△PQR∽△ABC∴ ,即∴AB=4.2(m),即树高为4.2m.考点解析【5-1】如图，小明在打网球时，要使球恰好能打过网，而且落在离网5米的位置上，则拍击球的高度应h为( )A.2.7米 B.1.8米 C.0.9米 D.0.6米 A迁移应用【5-2】如图，小明同学跳起来把一个排球打在离地2m远的地上，然后反弹碰到墙上，如果她跳起击球时的高度是1.8m，排球落地点离墙的距离是6m，假设球一直沿直线运动，球能碰到墙面离地多高的地方？解：∵∠ABO=∠CDO=90°，∠AOB=∠COD，∴△AOB∽△COD.解得 CD=5.4m.故球能碰到墙面离地5.4m高的地方．迁移应用【5-3】九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,如图，已知标杆高度CD=3m，标杆与旗杆的水平距离BD=15m,人的眼睛到地面的高度EF=1.6m，人与标杆CD的水平距离DF=2m，求旗杆AB的高度.迁移应用例10.如图，在△ABC中，AB=80，高CD=60,矩形EFGH中E、F在AB边上，G在BC边上，H在三角形内，且EF:GF=2:1.(1)在△ABC内画出矩形GFEH的位似图形，使其顶点在△ABC的边上(保留作图痕迹);(2)求所作的矩形的面积.解: (1)如图，矩形IJLK即为所作;考点解析例10.如图，在△ABC中，AB=80，高CD=60,矩形EFGH中E、F在AB边上，G在BC边上，H在三角形内，且EF:GF=2:1.(2)求所作的矩形的面积. 考点解析例11.如图，在平面直角坐标系中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为1:3，点A，B，E在x轴上.(1)若点F的坐标为(4.5, 3),直接写出点A和点C的坐标;(2)若正方形BEFG的边长为6，求点C的坐标. 考点解析例11.如图，在平面直角坐标系中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为1:3，点A，B，E在x轴上.(1)若点F的坐标为(4.5, 3),直接写出点A和点C的坐标;(2)若正方形BEFG的边长为6，求点C的坐标.解:(2)∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，相似比是1:3，正方形BEFG的边长为6∴正方形ABCD的边长为2，OB:0E=1:3∴0B:(0B+6)=1:3,解得0B=3∴点C的坐标为(3，2)考点解析 B迁移应用【6-2】在平面直角坐标系中，△ABC和△A1B1C1的相似比等于0.5，并且它们是关于原点O的位似图形，若点A的坐标为(2，4)，则其对应点A1的坐标是________________.【6-3】如图，是△AOB和把它放大后得到的△COD，则△AOB与△COD的相似比为______.(4，8)或(-4，-8) 迁移应用 D迁移应用