人教版数学九年级下册 27.2.5 《相似三角形的应用列举》课件（含动画演示）+分层练习（含答案解析）

这是一份人教版数学九年级下册 27.2.5 《相似三角形的应用列举》课件（含动画演示）+分层练习（含答案解析），文件包含2725相似三角形的应用列举课件pptx、例3mp4等2份课件配套教学资源，其中PPT共24页， 欢迎下载使用。

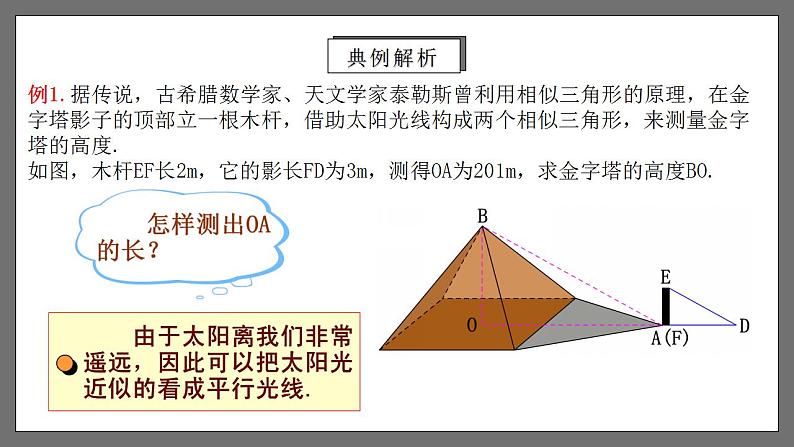
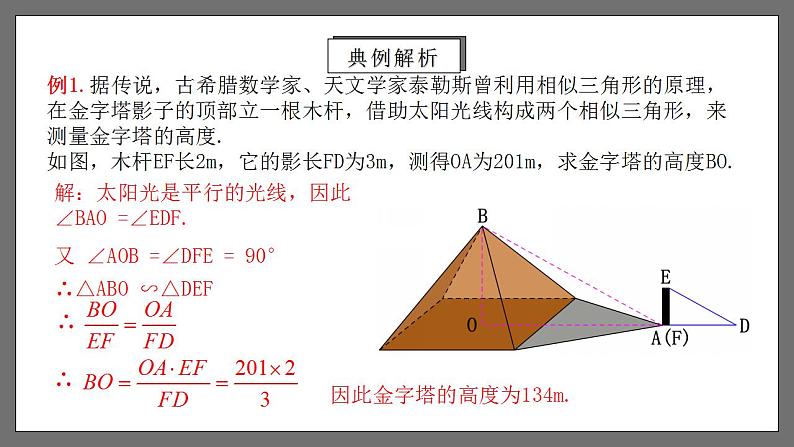
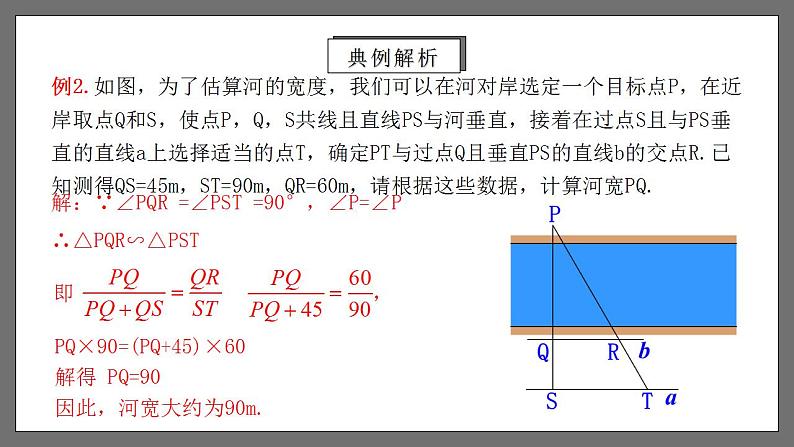
相似三角形的应用列举1.能够利用相似三角形的知识，求出不能直接测量的物体的高度和宽度. (重点)2. 进一步了解数学建模思想，能够将实际问题转化为相似三角形的数学模型，提高分析问题、解决问题的能力. (难点)学习目标1.相似三角形的判定：2.相似三角形的性质：(1) 通过平行线；(2) 三边成比例；(3) 两边成比例且夹角相等；(4) 两角分别相等.(1) 对应边成比例，对应角相等；(2) 相似三角形对应高的比，对应中线的比与对应角平分线的比都等于相似比；(3) 相似三角形周长的比等于相似比；(4) 相似三角形面积的比等于相似比的平方.复习回顾例1.据传说，古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理，在金字塔影子的顶部立一根木杆，借助太阳光线构成两个相似三角形，来测量金字塔的高度.如图，木杆EF长2m，它的影长FD为3m，测得OA为201m，求金字塔的高度BO.典例解析例1.据传说，古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理，在金字塔影子的顶部立一根木杆，借助太阳光线构成两个相似三角形，来测量金字塔的高度.如图，木杆EF长2m，它的影长FD为3m，测得OA为201m，求金字塔的高度BO.解：太阳光是平行的光线，因此 ∠BAO =∠EDF.又 ∠AOB =∠DFE = 90°∴△ABO ∽△DEF因此金字塔的高度为134m.典例解析表达式：物1高 ：物2高 = 影1长 ：影2长测量不能到达顶部的物体的高度，可以用“在同一时刻物高与影长成正比例”的原理解决.利用相似三角形测量高度总结提升在某一时刻，测得一根高为1.8m的竹竿的影长为3m，同时测得一栋楼的影长为90m，这栋楼的高度是多少？针对练习例2.如图，为了估算河的宽度，我们可以在河对岸选定一个目标点P，在近岸取点Q和S，使点P，Q，S共线且直线PS与河垂直，接着在过点S且与PS垂直的直线a上选择适当的点T，确定PT与过点Q且垂直PS的直线b的交点R.已知测得QS=45m，ST=90m，QR=60m，请根据这些数据，计算河宽PQ.PQ×90=(PQ+45)×60解得 PQ=90因此，河宽大约为90m.解：∵∠PQR =∠PST =90°，∠P=∠P∴△PQR∽△PST典例解析如图，测得BD=120m，DC=60m，EC=50m，求河宽AB.解：∵ AB⊥BC，CE⊥BC ∴ ∠B=∠C=90° 又 ∠ADB=∠EDC ∴ △ABD∽△ECD∴ 即 解得，AB=100 因此，河宽AB为100m.针对练习测量如河宽等不易直接测量的物体的宽度，常构造相似三角形求解. 利用相似三角形测量河宽总结提升例3.如图，左、右并排的两棵大树的高分别是 AB = 8 m 和 CD = 12 m，两树底部的距离 BD = 5 m，一个人估计自己眼睛距离地面 1.6 m，她沿着正对这两棵树的一条水平直路 l 从左向右前进，当她与左边较低的树的距离小于多少时，就看不到右边较高的树的顶端C 了? 分析：如图，设观察者眼睛的位置为点F，画出观察者的水平视线FG，分别交AB、CD于点H、K.视线FA与FG的夹角∠AFH是观察点A时的仰角.类似地，∠CFK是观察点C时的仰角.由于树的遮挡，区域Ⅰ和Ⅱ，观察者都看不到.典例解析解：如图，假设观察者从左向右走到点E时，她的眼睛的位置点E与两树的顶端A、C恰在一条直线上. ∵ AB⊥l，CD⊥l，∴ AB∥CD ∴ △AEH∽△CEK∴ 即 ，解得 EH=8(m)由此可知，如果观察者继续前进，当她与左边的树的距离小于8m时，由于这棵树的遮挡，她看不到右边树的顶端C.典例解析1.某校数学兴趣小组为测量学校旗杆AC的高度，在点F处竖立一根长为1.5米的标杆DF，如图所示，量出DF的影子EF的长度为1米，再量出旗杆AC的影子BC的长度为6米，那么旗杆AC的高度为( )A.6米 B.7米 C.8.5米 D.9米 D达标检测2.如图，小明在打网球时，要使球恰好能打过网，而且落在离网5米的位置上，则拍击球的高度应h为( )A.2.7米 B.1.8米 C.0.9米 D.0.6米 A达标检测3.如图，铁道口的栏杆短臂长1m，长臂长16m，当短臂端点下降0.5m时，长臂端点升高______m.8达标检测4.如图是小玲设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜，光线从点A出发经平面镜反射后，刚好射到古城墙CD的顶端C处.已知AB⊥BD，CD⊥BD.且测得AB=1.4m，BP=2.1m，PD=12m.那么该古城墙CD的高度是_____m.8达标检测5.如图，路灯距离地面8m，身高1.6m的小明站在距离灯的底部(点O)20m的A处，则小明的影子AM长_____m5达标检测6.如图，一高1m的油桶内有一定量的油，为了测出桶内油的深度，用一根长1.2m的木棒从桶盖小口斜插入桶内，一端到桶底，另一端正好到小口，抽出木棒，量得棒上浸油部分长0.45m，则桶内油的深度为________m.0.375达标检测7.九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,如图，已知标杆高度CD=3m，标杆与旗杆的水平距离BD=15m,人的眼睛到地面的高度EF=1.6m，人与标杆CD的水平距离DF=2m，求旗杆AB的高度.达标检测8.教学楼旁边有一棵树，课外数学兴趣小组在阳光下，测得一根长为1m的竹竿的影长为0.9m,但他们马上测树的影长时，发现树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上，如图所示.经过一番争论，该小组的同学认为继续测量也可以求出树高，他们测得落在地面.上的影长为2.7m，落在墙璧上影长为1.2m，请你和他们一起计算一下， 树高为多少?达标检测解:根据题意，画出示意图，延长AD、BE相交于C,则CE是无墙壁遮挡时树影长的一部分.∴ ,即∴CE=1.08(m)∴BC=BE+CE=2.7+1.08=3.78(m)又∵△PQR∽△ABC∴ ,即∴AB=4.2(m),即树高为4.2m.达标检测9.李师傅用镜子测量一棵古树的高，但树旁有一条小河,不便测量镜子与树之间的距离，于是他两次利用镜子.第一次把镜子放在C点(如图所示)，人在F点正好在镜中看到树尖A;第二次他把镜子放在C′处，人在F′处正好看到树尖A.已知李师傅眼睛距地面的高度为1.7m,量得CC′为12m， CF为1.8m， C′ F′为3.84m,，求树高.达标检测达标检测