八年级下册第十八章 平行四边形18.2 特殊的平行四边形18.2.3 正方形一等奖ppt课件

这是一份八年级下册第十八章 平行四边形18.2 特殊的平行四边形18.2.3 正方形一等奖ppt课件，共18页。

1．正方形具有而菱形不一定具有的性质是( )A．对角线互相平分 B．对角线相等C．对角线互相垂直 D．对角线平分一组对角2．(例5变式)如图，在正方形ABCD中，对角线AC，BD相交于点O，则图中的等腰直角三角形有( )A．4个 B．6个 C．8个 D．10个
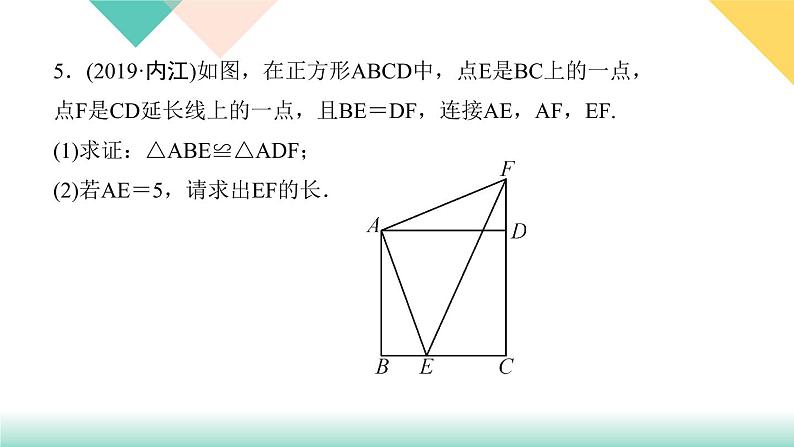
5．(2019·内江)如图，在正方形ABCD中，点E是BC上的一点，点F是CD延长线上的一点，且BE＝DF，连接AE，AF，EF.(1)求证：△ABE≌△ADF；(2)若AE＝5，请求出EF的长．
6．(内江中考)下列命题中，真命题是( )A．对角线相等的四边形是矩形B．对角线互相垂直的四边形是菱形C．对角线互相平分的四边形是平行四边形D．对角线互相垂直平分的四边形是正方形7．已知四边形ABCD是平行四边形，下列条件：①AB＝BC；②∠ABC＝90°；③AC＝BD；④AC⊥BD.选两个作为补充条件，使得四边形ABCD是正方形，其中错误的选法是( )A．①② B．②③ C．①③ D．③④
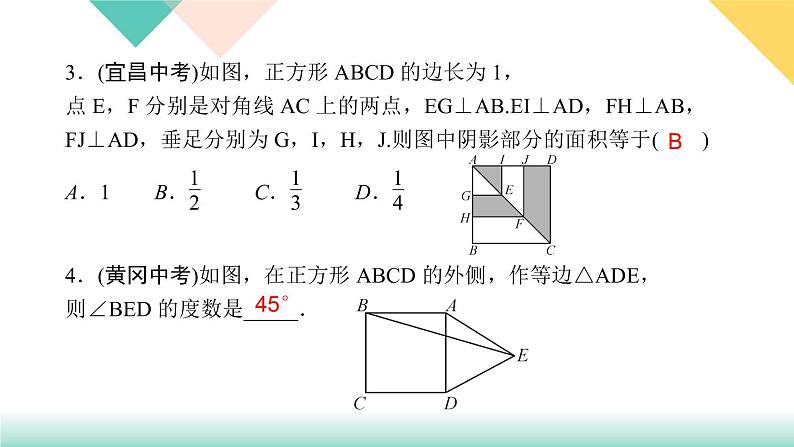
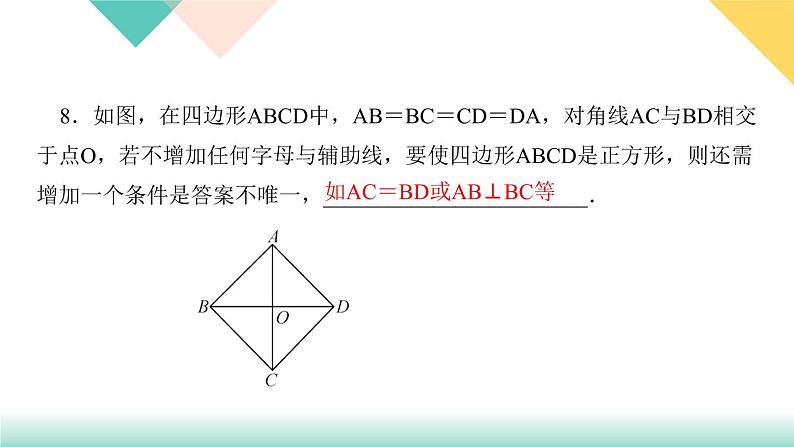
8．如图，在四边形ABCD中，AB＝BC＝CD＝DA，对角线AC与BD相交于点O，若不增加任何字母与辅助线，要使四边形ABCD是正方形，则还需增加一个条件是答案不唯一，________________________．
如AC＝BD或AB⊥BC等
9．如图，在△ABC中，AB＝AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F.(1)求证：△BED≌△CFD；(2)若∠A＝90°，求证：四边形DFAE是正方形．解：(1)∵AB＝AC，∴∠B＝∠C，∵DE⊥AB，DF⊥AC，∴∠BED＝∠CFD＝90°，∵D为BC中点，∴BD＝CD，∴△BED≌△CFD(AAS)(2)∵∠A＝∠DEA＝∠DFA＝90°，∴四边形DFAE是矩形，由(1)知△BED≌△CFD，∴DE＝DF，∴四边形DFAE是正方形
12．(2019·菏泽)如图，E，F是正方形ABCD的对角线AC上的两点，AC＝8，AE＝CF＝2，则四边形BEDF的周长是____．
13．如图，点O是线段AB上的一点，OA＝OC，OD平分∠AOC交AC于点D，OF平分∠COB，CF⊥OF于点F.(1)求证：四边形CDOF是矩形；(2)当∠AOC为多少度时，四边形CDOF是正方形？并说明理由．解：(1)证四边形CDOF的三个角都为直角　(2)∠AOC＝90°时，四边形CDOF是正方形，理由：易得AD＝DC，∵∠AOC＝90°，∴OD＝DC，由(1)知四边形CDOF是矩形，∴四边形CDOF是正方形
14．(2019·甘肃)如图，在正方形ABCD中，点E是BC的中点，连接DE，过点A作AG⊥ED交DE于点F，交CD于点G.(1)证明：△ADG≌△DCE；(2)连接BF，证明：AB＝FB.
15．如图，在Rt△ABC中，∠ACB＝90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于点E，垂足为F，连接CD，BE.(1)求证：CE＝AD；(2)当D在AB中点时，四边形BECD是什么特殊四边形？说明你的理由；(3)若D为AB中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？请说明你的理由．