浙教版数学九年级上册第一章《二次函数 章末复习----确定二次函数的表达式》 课件

这是一份浙教版数学九年级上册第一章《二次函数 章末复习----确定二次函数的表达式》 课件，共18页。
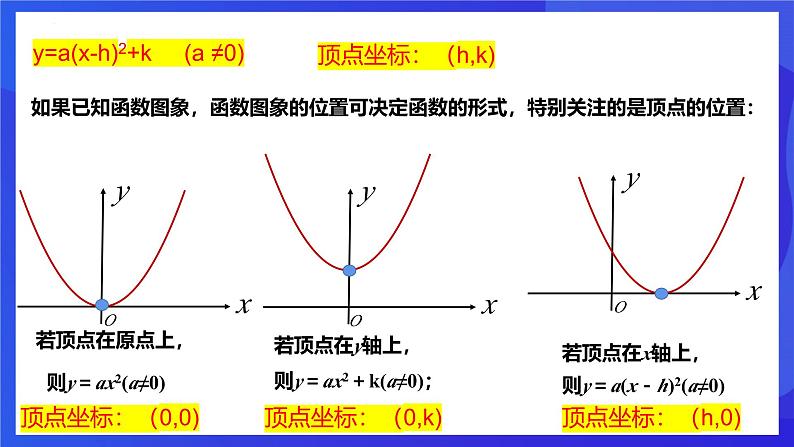
第一章 二次函数章末复习 确定二次函数的表达式 1.一元二次方程的一般形式：ax2＋bx＋c＝0(a≠0)；2.一元二次方程根的判别式：3.一元二次方程的求根公式：4.一元二次方程的根的情况： 方程有两个不相等的实数根方程有两个相等的实数根方程没有实数根齐声朗读x1+x2=  一元二次方程的根与系数的关系 如果 ax2+bx+c=0(a≠0)的两个根为x1， x2，那么【特别强调】满足上述关系的前提条件：b2-4ac≥0. 韦达（1540——1603）是法国数学家,最早发现代数方程的根与系数之间有这种关系，因此，人们把这个关系称为韦达定理。y＝ax2＋bx＋c你想到了什么？二次函数的第三种表达交点式：当二次函数y＝ax2＋bx＋c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2＋bx＋c=0的根.1.二次函数表达式的一般形式： 二次函数表达式的顶点式： 3.若二次函数y=ax²+bx+c(a≠0)与x轴两交点为(x1,0),(x2,0) 则其函数表达式可以表示成：y=ax²+bx+c (a,b,c为常数,a ≠0)y=a(x-h)2+k (a ≠0)y=a(x-x1)(x-x2) (a ≠0)顶点坐标：（h,k)交点式（两根式）知识小结 用待定系数法确定二次函数关系式的一般步骤和运用的思想方法. 如果已知函数图象，函数图象的位置可决定函数的形式，特别关注的是顶点的位置：若顶点在原点上， 若顶点在y轴上，若顶点在x轴上， 则y＝ax2(a≠0)则y＝ax2＋k(a≠0)；则y＝a(x－h)2(a≠0)y=a(x-h)2+k (a ≠0)顶点坐标：（h,k)顶点坐标：（0,0)顶点坐标：（0,k)顶点坐标：（h,0)二次函数的表达式中有几个待定的字母，就需要有几个条件去求解；反过来，要根据题目中给定的条 件数目去设相应的函数表达式并求解，这种方法叫待定系数法． 用待定系数法确定二次函数关系式的一般步骤和运用的思想方法. 1. 如图，已知 抛物线的顶点在坐标原点，矩形ABCD的顶点A，D在抛物线上，且AD平行于 x轴，交y轴于点F，AB的中点E在x轴上，B点的坐标为(2，1)，求此抛物线对应的函数表达式  2、已知二次函数的图象经过（1,0）、（2,0）、（0,2）三点， 求该函数的解析式法1：一般式:y=ax2+bx+c   y=x2-3x+2法2：交点式（两根式）:y=a(x-x1)(x-x2)y=a(x-1)(x-2)2=a(0-1)(0-2)a=1y=(x-1)(x-2)y=x2-3x+2法3：顶点式:y=a（x-h）2+k  3、如图，是一条抛物线的图象，求其解析式A（-1,0）、B（3,0）、 C（0,-3） 法1：一般式:y=ax2+bx+c   y=x2-2x-3法2：交点式（两根式）:y=a(x-x1)(x-x2)y=a(x+1)(x-3)-3=a(0+1)(0-3)a=1y=(x+1)(x-3)y=x2-2x-3法3：顶点式:y=a（x-h）2+ky=a（x- 1）2+k  y=（x- 1 ）2 - 44、如图，是一条抛物线的图象，求其解析式A（0,2）、 B（2,0）、 对称轴：直线x=0.5 法1：一般式:y=ax2+bx+c   y=-x2+x+2法2：交点式（两根式）:y=a(x-x1)(x-x2)y=a(x+1)(x-2)C（-1,0） 2=a(0+1)(0-2)a=-1y=-(x+1)(x-2)y=-x2+x+2法3：顶点式:y=a（x-h）2+ky=a（x- 0.5）2+k  y= -（x- 0.5）2 +2.255.若二次函数图象过A(2,-4),B(0,2), C(-1,2)三点 ,求此函数的解析式。 6.篮球运动员投篮时，球运动的路线为抛物线的一部分（如图）， 抛物线的对称轴为x=2.5. 求：⑴ 球运动路线的函数解析式和自变量的取值范围；⑵ 球在运动中离地面的最大高度。解: ⑴设函数解析式为:y=a(x－2.5)2+k, 根据题意，得：则：a=－0.2,k=3.5∴解析式为:y=－0.2x2+x+2.25,自变量x的取值范围为：0≤x≤4.⑵球在运动中离地面的最大高度为3.5米。 7.已知一个二次函数的图象经过点(4,-3)，并且当x=3时有最大值4，试确定这个二次函数的解析式。解法2：（利用顶点式）∵  当x=3时，有最大值4∴  顶点坐标为(3,4) 设二次函数解析式为：   y=a(x-3)2+4∵  函数图象过点（4，- 3）∴  a(4 - 3)2 +4 = - 3∴  a= -7∴ 二次函数的解析式为： y= -7(x-3)2+41．用待定系数法求二次函数的表达式：(1)若给出抛物线上任意三点，通常可设一般式y＝ax2＋bx＋c(a≠0)．(2)若给出抛物线的顶点坐标或对称轴或最值，通常可 设顶点式y＝a(x－h)2＋k(a≠0)．(3)若给出抛物线与x轴的交点或与x轴的交点距离，通常可设交点式y＝a(x－x1)(x-x2)(a≠0)．要点精析：(1)求二次函数表达式的几种方法之间是相互联系的，而不是孤立的，不同的设法是根据不同的已知条件来确定的．归纳小结课程结束