浙教版初中数学九年级上册第一单元《二次函数》单元测试卷（标准难度）（含答案解析）

浙教版初中数学九年级上册第一单元《二次函数》单元测试卷

考试范围：第一章  考试时间 ：120分钟  总分 ：120分

第I卷（选择题）

一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）

1.  若是二次函数，则的值是(    )

A.  B.  C.  D. 或

2.  对于关于的函数，下列说法错误的是(    )

A. 当时，该函数为正比例函数
B. 当时，该函数为一次函数
C. 当该函数为二次函数时或
D. 当该函数为二次函数时，

3.  已知是关于的二次函数，那么的值为(    )

A.  B.  C.  D.

4.  如图，抛物线过点和点，且顶点在第四象限，设，则的取值范围是(    )

 

A.  B.  C.  D.

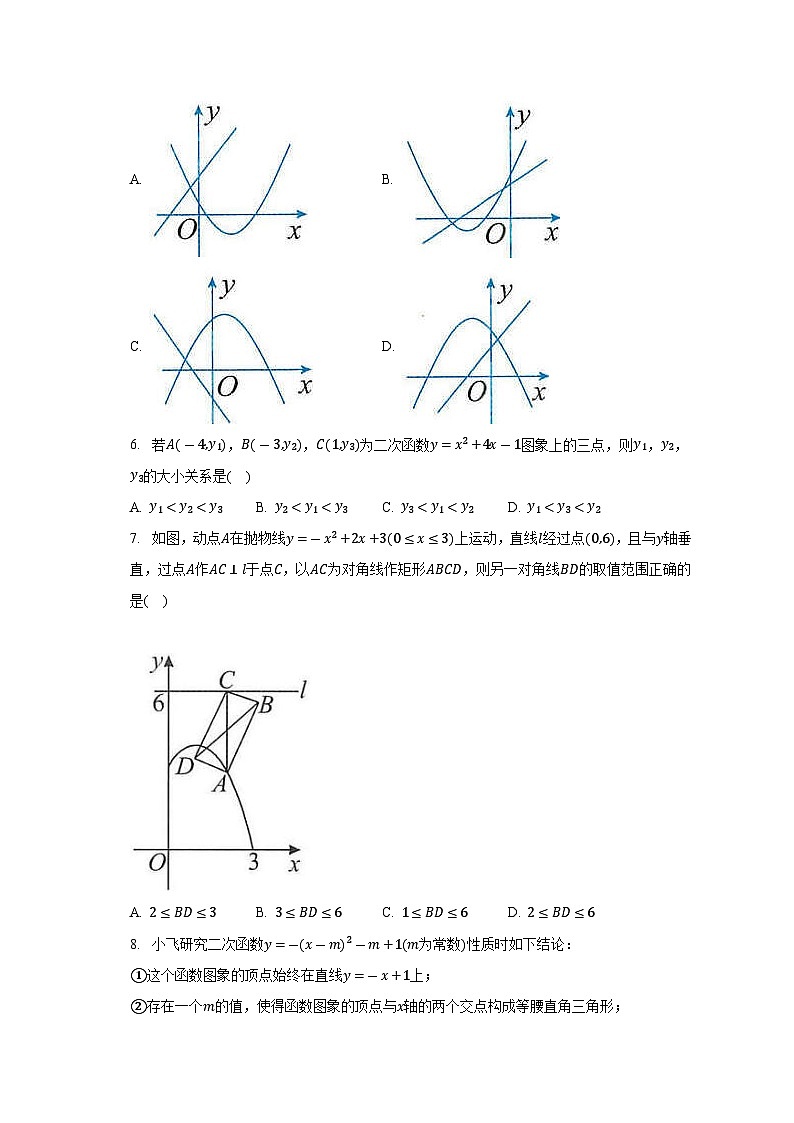
5.  一次函数与二次函数在同一平面直角坐标系中的图象可能是(    )

A.  B.
C.  D.

6.  若，，为二次函数图象上的三点，则，，的大小关系是(    )

A.  B.  C.  D.

7.  如图，动点在抛物线上运动，直线经过点，且与轴垂直，过点作于点，以为对角线作矩形，则另一对角线的取值范围正确的是(    )

 

A.  B.  C.  D.

8.  小飞研究二次函数为常数性质时如下结论：

这个函数图象的顶点始终在直线上；

存在一个的值，使得函数图象的顶点与轴的两个交点构成等腰直角三角形；

点与点在函数图象上，若，，则；

当时，随的增大而增大，则的取值范围为．

其中错误结论的序号是(    )

A.  B.  C.  D.

9.  在平面直角坐标系中，已知，设函数的图象与轴有个交点，函数的图象与轴有个交点，则(    )

A. 或 B. 或
C. 或 D. 或

10.  某超市对进货价为元千克的某种苹果的销售情况进行统计，发现每天销售量千克与销售价元千克存在一次函数关系，如图所示则最大利润是(    )

 

A.  B.  C.  D.

11.  如图是一个横断面为抛物线形状的拱桥，当水面在时，拱顶拱桥洞的最高点离水面，水面宽如图建立平面直角坐标系，则抛物线的解析式是(    )

A.  B.  C.  D.

12.  如图，游乐园里的原子滑车是很多人喜欢的项目，惊险刺激，原子滑车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分，原子滑车运行的竖直高度单位：与水平距离单位：近似满足函数关系如图记录了原子滑车在该路段运行的与的三组数据、、，根据上述函数模型和数据，可推断出，此原子滑车运行到最低点时，所对应的水平距离满足(    )

 

A.  B.  C.  D.

第II卷（非选择题）

二、填空题（本大题共4小题，共12.0分）

13.  将抛物线向上平移个单位长度后，经过点，则的值是______．

14.  在平面直角坐标系中，将抛物线先绕原点旋转，再向下平移个单位，所得到的抛物线的顶点坐标是          ．

15.  若点，，都在二次函数的图象上，则，，的大小关系为          用“”连接．

16.  如图是抛物线型拱桥，当拱顶离水面时，水面宽，水面下降，水面宽度增加_____．

 

三、解答题（本大题共9小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）

17.  本小题分

已知函数．

当为何值时，为的二次函数

当为何值时，为的一次函数

18.  本小题分

已知函数．

若这个函数是二次函数，求的取值范围

若这个函数是一次函数，求的值

这个函数可能是正比例函数吗为什么

19.  本小题分

已知二次函数．

将二次函数化为一般形式，并指出相应的，，的值

当时，求的值

当时，求的值．

20.  本小题分
如图，抛物线与轴相交于点、，且过点，连接、求的面积．

21.  本小题分
已知二次函数是常数的图象是抛物线．
求证：抛物线顶点在函数的图象上；
若点，在抛物线上，且，求的取值范围．

22.  本小题分
我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”．

求抛物线与轴的“和谐值”．

求抛物线与直线的“和谐值”．

若抛物线在抛物线的上方，且两条抛物线的“和谐值”为，求的值．

23.  本小题分
已知二次函数的图象以为顶点，且过点．

求该函数的表达式

求该函数图象与坐标轴的交点坐标．

24.  本小题分
已知二次函数的图象经过点和点．

分别求，的值，并指出二次函数图象的顶点、对称轴

当时，试求二次函数的最大值与最小值．

25.  本小题分
端午节是我国入选世界非物质文化遗产的传统节日，端午节吃粽子是中华民族的传统习俗市场上豆沙粽的进价比猪肉粽的进价每盒便宜元，某商家用元购进的猪肉粽和用元购进的豆沙粽盒数相同在销售中，该商家发现猪肉粽每盒售价元时，每天可售出盒；每盒售价提高元时，每天少售出盒．
求猪肉粽和豆沙粽每盒的进价；
设猪肉粽每盒售价元，表示该商家每天销售猪肉粽的利润单位：元，求关于的函数解析式并求最大利润．

答案和解析

1.【答案】 

【解析】解：是关于的二次函数，
，且，
．
故选：．
利用二次函数定义可得：，且，再计算出的值即可．
本题主要考查了二次函数定义，关键是掌握形如、、是常数，的函数，叫做二次函数．

2.【答案】 

【解析】【分析】
本题考查了正比例函数的概念、一次函数以及二次函数的概念 根据正比例函数的概念、一次函数的概念以及二次函数的概念，结合各选项分析即可 
【解答】
解：当时，该函数为，是正比例函数，选项说法正确，故此选项不符合题意；
B.当时，，该函数为，是一次函数，选项说法正确，故此选项不符合题意；
C.当该函数为二次函数时，且，解得，选项说法错误，故此选项符合题意；
D.当该函数为二次函数时，且，即，选项说法正确，故此选项不符合题意．
故选C．

3.【答案】 

【解析】【分析】
本题考查了二次函数的定义、绝对值的定义，利用二次函数的定义得出关于的方程是解题关键．根据形如是二次函数，可得答案．
【解答】
解：由是关于的二次函数，
得且．
解得．
故选B．

4.【答案】 

【解析】略

5.【答案】 

【解析】略

6.【答案】 

【解析】略

7.【答案】 

【解析】略

8.【答案】 

【解析】解：二次函数为常数
顶点坐标为且当时，
这个函数图象的顶点始终在直线上
故结论正确；
假设存在一个的值，使得函数图象的顶点与轴的两个交点构成等腰直角三角形
令，得，其中
解得：，
顶点坐标为，且顶点与轴的两个交点构成等腰直角三角形
解得：或
当时，二次函数，此时顶点为，与轴的交点也为，不构成三角形，舍去；
存在，使得函数图象的顶点与轴的两个交点构成等腰直角三角形
故结论正确；
二次函数为常数的对称轴为直线
点离对称轴的距离小于点离对称轴的距离
，且
故结论错误；
当时，随的增大而增大，且
的取值范围为．
故结论正确．
故选：．
根据函数解析式，结合函数图象的顶点坐标、对称轴以及增减性依次对个结论作出判断即可．
本题主要考查了二次函数图象与二次函数的系数的关系，是一道综合性比较强的题目，需要利用数形结合思想解决本题．

9.【答案】 

【解析】【分析】
本题主要考查一次函数和二次函数与轴的交点问题，关键是根据根的判别式的取值确定抛物线与轴的交点个数，二次项系数为字母的代数式时，要根据系数是否为，确定它是什么函数，进而确定与轴的交点个数．
先把两个函数化成一般形式，若为二次函数，再计算根的判别式，从而确定图象与轴的交点个数，若一次函数，则与轴只有一个交点，据此解答．
【解答】
解：，
，
函数的图象与轴有个交点，
，
函数，
当时，，函数的图象与轴有个交点，即，此时；
当时，不妨令，，，函数为一次函数，与轴有一个交点，即，此时；
综上可知，或．
故选：．

10.【答案】 

【解析】略

11.【答案】 

【解析】解：设出抛物线方程，
由图象可知该图象经过点，
故，
，
故，
故选：．
设出抛物线方程代入坐标求得．
本题主要考查二次函数的应用，解题的关键是熟练掌握待定系数法求函数解析式．

12.【答案】 

【解析】【分析】
此题考查了二次函数的应用，此题也可以将所求得的抛物线解析式利用配方法求得顶点式方程，然后直接得到抛物线顶点坐标，由顶点坐标推知此原子滑车运行到最低点时，所对应的水平距离．
将点、、分别代入函数解析式，求得系数的值；然后由抛物线的对称轴公式可以得到答案．
【解答】
解：根据题意知，抛物线经过点、、，
则，
解得：，
所以．
此原子滑车运行到最低点时，所对应的水平距离满足．
故选：．

13.【答案】 

【解析】【分析】
本题考查了二次函数图象的平移，二次函数图象上点的坐标特征，解题的关键是得出平移后的表达式．
根据二次函数图象的平移得出平移后的表达式，再将点代入，得到，最后将变形求值即可．
【解答】
解：将抛物线向上平移个单位长度后，
表达式为：，
即，
抛物线经过点，
代入得：，即，
，
故答案为：．

14.【答案】 

【解析】略

15.【答案】 

【解析】略

16.【答案】 

【解析】【分析】
此题主要考查了二次函数的应用，根据已知建立坐标系从而得出二次函数解析式是解决问题的关键．
根据已知建立平面直角坐标系，进而求出二次函数解析式，再通过把代入抛物线解析式得出水面宽度，即可得出答案．
【解答】解：建立平面直角坐标系，设横轴通过，纵轴通过中点且通过点，则通过画图可得知为原点，

抛物线以轴为对称轴，且经过，两点，，抛物线顶点坐标为，
通过以上条件可设顶点式，代入点坐标到抛物线解析式得出：，所以抛物线解析式为，
当水面下降，通过抛物线在图上的观察可转化为：
当时，对应的抛物线上两点之间的距离，也就是直线与抛物线相交的两点之间的距离，
把代入抛物线解析式得出：，
解得：，
所以水面宽度增加到，比原先的宽度增加了，
故答案为：．

17.【答案】解：根据题意得且，

解得，即当为时，是的二次函数

当且，即时，是的一次函数

当且时，是的一次函数，解得

当且时，是的一次函数，解得．

综上，当为或或时，是的一次函数．

【解析】【分析】
本考查了二次函数的定义、一次函数的定义．
根据二次函数的定义得到得且，然后解不等式和方程即可得到满足条件的的值
根据一次函数的定义分类讨论：当时，是的一次函数当且时，是的一次函数当且时，是的一次函数，然后分别解方程或不等式即可．

18.【答案】解：函数，若这个函数是二次函数，则，解得且

若这个函数是一次函数，则，，解得．

这个函数不可能是正比例函数当此函数是一次函数时，，而此时

【解析】本题考查了二次函数，一次函数和正比例函数的定义，注意二次函数的二次项系数不能等于时，是二次函数；二次函数的二次项系数等于时，是一次函数；二次项系数等于，同时常数项等于时，是正比例函数．
根据二次函数的二次项系数不等于，可得答案；
根据二次函数的二次项系数等于，常数项不等于，是一次函数，可得答案；根据二次函数的二次项系数等于，常数项等于，可得正比例函数．

19.【答案】．

其中，，．

当时，．

当时，，解得或．

【解析】【分析】
本题主要考查二次函数的表达式，一元二次方程的解法以及求函数值，掌握代数式求值以及解一元二次方程的方法是解题的关键．
二次函数一般形式为，将题目按照其形式进行转化；
将代入表达式中，进行计算；
将代入表达式中，解一元二次方程即可．

20.【答案】解：抛物线经过点，
，
令，则，
解得，，
，，
． 

【解析】将点代入抛物线表达式，求出值，再求出点和点的横坐标，求出，，可得，利用三角形面积公式计算即可．
本题考查了二次函数图象上的点，抛物线与轴交点坐标，三角形的面积，解题的关键是正确求出各点坐标．

21.【答案】证明：，
抛物线的顶点坐标为，
当时，，
抛物线顶点在函数的图象上；
解：抛物线开口向上，对称轴为直线，
当时，；
当时，，
，

解得． 

【解析】将抛物线的解析式化为顶点式，将顶点横坐标代入函数求出的值，与顶点纵坐标比较即可得到答案；
由点、点的横坐标求出、，进而列不等式求解．
此题考查了二次函数图象上点的坐标特征，解题的关键是掌握二次函数图象与系数的关系，掌握二次函数与方程的关系．

22.【答案】【小题】

【小题】

．

【小题】

．

【解析】 略
 略
 略

23.【答案】【小题】

由为抛物线顶点，

设抛物线解析式为，

将点代入，得，

解得．

【小题】

令，则，令，则．

抛物线与轴的交点坐标为，

与轴的交点坐标为，．

【解析】 见答案
 见答案

24.【答案】【小题】

根据题意，将点和点代入，
得解得

二次函数的表达式为，

该二次函数图象的顶点坐标为，一，对称轴为

【小题】

在中，由知当时，取得最小值，

当时，取得最大值，

最大值，最小值．

【解析】 见答案
 见答案

25.【答案】解：设猪肉粽每盒进价元，则豆沙粽每盒进价元，
则，
解得：，经检验是方程的解，
猪肉每盒进价元，豆沙粽每盒进价元，
答：猪肉每盒进价元，豆沙粽每盒进价元；
由题意得，当时，每天可售出盒，
当猪肉粽每盒售价元时，每天可售盒，
，
配方，得：，
时，随的增大而增大，
当时，取最大值，最大值为：元．
答：关于的函数解析式为，且最大利润为元． 

【解析】本题考查了二次函数的应用以及分式方程的应用，关键是根据题意列出每天销售猪肉粽的利润与猪肉粽每盒售价元的函数关系式．
设猪肉粽每盒进价元，则豆沙粽每盒进价元，根据商家用元购进的猪肉粽和用元购进的豆沙粽盒数相同列出方程，解方程即可；
由题意得，当时，，每天可售出盒，当猪肉粽每盒售价元时，每天可售盒，列出每天销售猪肉粽的利润与猪肉粽每盒售价元的函数关系式，根据二次函数的性质及的取值范围求利润的最大值．