2025高考数学一轮复习-第4章-三角函数与解三角形-第8讲 余弦定理、正弦定理的综合应用【课件】

这是一份2025高考数学一轮复习-第4章-三角函数与解三角形-第8讲 余弦定理、正弦定理的综合应用【课件】，共58页。PPT课件主要包含了教材再现四基诊断，测量中的几个有关术语，重点串讲能力提升，三角形面积计算，解三角形的应用举例等内容，欢迎下载使用。
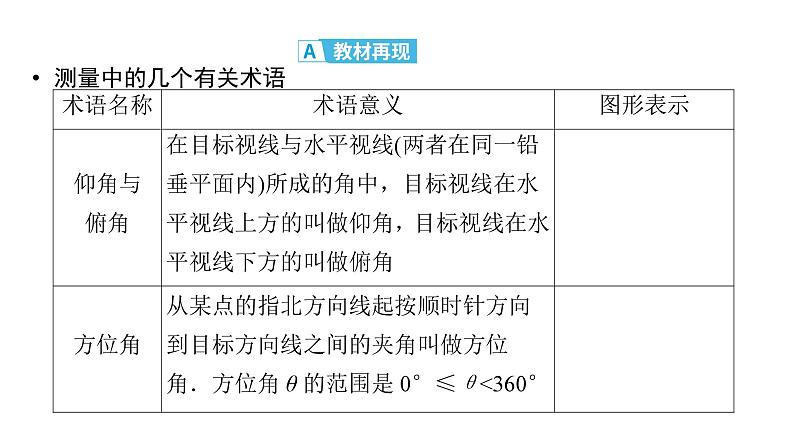
课程标准　能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题．
3．在某次海军演习中，已知甲驱逐舰在航母的南偏东15°方向且与航母的距离为12海里，乙护卫舰在甲驱逐舰的正西方向，若测得乙护卫舰在航母的南偏西45°方向，则甲驱逐舰与乙护卫舰的距离为________海里．
三角形中的最值与范围问题
解三角形中最值(范围)问题的解题策略利用正弦、余弦定理以及面积公式化简整理，构造关于某一个角或某一条边的函数或不等式，利用函数的单调性或基本不等式等求最值(范围).
解决距离问题的两个注意事项(1)选定或确定要创建的三角形，首先确定所求量所在的三角形，若其他量已知，则直接求解；若有未知量，则把未知量放在另一个确定的三角形中求解．(2)确定用正弦定理还是余弦定理，如果都可以用，就选便于计算的定理，选定合适的三角形．
解决高度问题的关注点(1)在处理有关高度问题时，理解仰角、俯角(在铅垂面上所成的角)、方向(位)角(在水平面上所成的角)是关键．(2)注意山或塔垂直于地面或海平面，把空间问题转化为平面问题．
(2024·河南濮阳模拟)如图所示，A，B，C是相隔不远的三座山峰的峰顶，地理测绘员要在A，B，C三点进行测量，在C点测得B点的仰角为30°，B与C的海拔高度相差180 m；在B点测得A点的仰角为45°.设A，B，C在同一水平面上的射影分别为A′，B′，C′，且∠A′C′B′＝∠A′B′C′＝30°，则A与C两点的海拔高度差为________m．
作BE⊥AA′，CF⊥AA′，则∠ABE＝45°，所以AE＝BE＝A′B′＝180 m．所以A与C两点的海拔高度差AF＝BD＋AE＝360(m).
角度3　角度问题例5　图1是南北方向水平放置的圭表(一种度量日影长的天文仪器，由“圭”和“表”两个部件组成)的示意图，其中表高为h，日影长为l.图2是地球轴截面的示意图，虚线表示点A处的水平面．已知某测绘兴趣小组在冬至日正午时刻(太阳直射点的纬度为南纬23°26′)，在某地利用一表高为2 dm的圭表按图1方式放置后，测得日影长为2.98 dm，则该地的纬度约为北纬(参考数据：tan 34°≈0.67，tan 56°≈1.48)(　　)A.23°26′ B．32°34′C.34° D．56°
解决角度问题的三个注意事项(1)测量角度时，首先应明确方位角及方向角的含义；(2)求角的大小时，先在三角形中求出其正弦或余弦值；(3)在解应用题时，要根据题意正确画出示意图，通过这一步可将实际问题转化为可用数学方法解决的问题，解题过程中也要注意体会正弦、余弦定理综合使用的优点．
因为AD＞AC，故∠CDA为锐角，所以∠CDA＝60°，即此时灯塔C位于游轮的南偏西60°方向上．