初中数学北师大版（2024）八年级上册5 三角形的内角和定理课文ppt课件

这是一份初中数学北师大版（2024）八年级上册5 三角形的内角和定理课文ppt课件，共22页。PPT课件主要包含了学习目标，情境导入，探索交流，例题解析，还有其他证明方法吗，练习巩固等内容，欢迎下载使用。
1.了解并掌握三角形的外角的定义．（重点）2.掌握三角形的外角的性质，利用外角的性质进行简单的证明和计算．（难点）
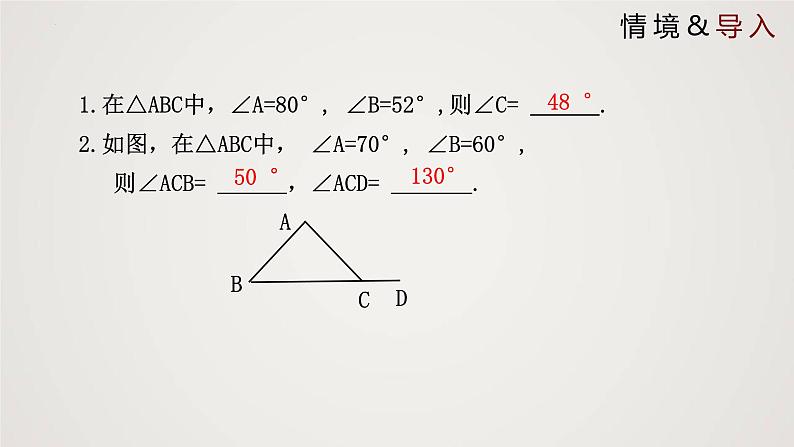
1.在△ABC中，∠A=80°, ∠B=52°,则∠C= .
2.如图，在△ABC中， ∠A=70°, ∠B=60°, 则∠ACB= ，∠ACD= .
问题 发现懒羊羊独自在O处游玩后，灰太狼打算用迂回的方式，先从A前进到C处，然后再折回到B处截住懒羊羊返回羊村的去路，红太狼则直接在A处拦截懒羊羊，已知∠BAC=40°， ∠ABC=70°.灰太狼从C处要转多少度角才能直达B处？
利用“三角形的内角和为180°”来求∠BCD，你会吗？
思考 像∠BCD这样的角有什么特征吗？猜想它的性质.这节课让我们一起来探讨吧.
由三角形内角和易得∠BCA=180°－∠A－∠CBA=70°，所以∠BCD=180°－∠BCA=110°.
三角形外角的定义：三角形内角的一条边与另一条边的反向延长线组成的角，称为三角形的外角.如图1，∠ACD是△ABC的∠ACB的外角.
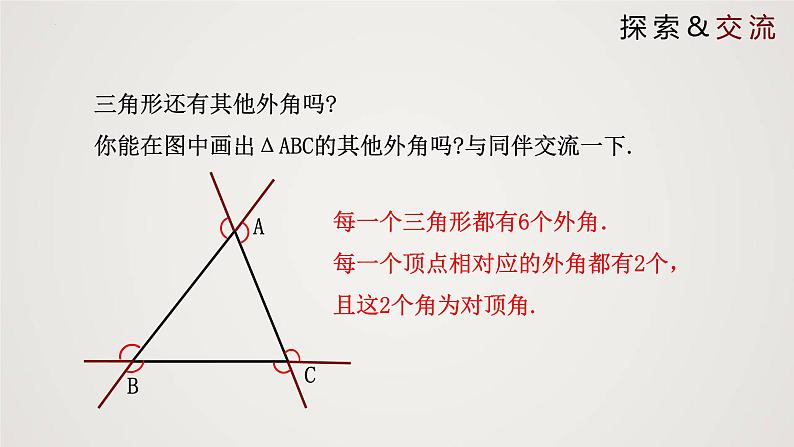
三角形还有其他外角吗?你能在图中画出ΔABC的其他外角吗?与同伴交流一下.
每一个三角形都有6个外角．每一个顶点相对应的外角都有2个，且这2个角为对顶角.
总结：三角形的外角应具备的条件：
①角的顶点是三角形的顶点；②角的一边是三角形的一边；③另一边是三角形中一边的延长线.
∠ACD是△ABC的一个外角
每一个三角形都有6个外角．
在图中，∠1与其他角有什么关系？能证明你的结论吗?
我们发现∠1+∠4=180°,依据是平角的定义.我们发现∠1=∠2+∠3. 理由是:∵∠2+∠3+∠4=180°(三角形内角和定理),∠1+∠4=180°(平角的定义),∴∠1=∠2+∠3.
以上内容你们能得出什么结论?三角形的一个外角等于和它不相邻的两个内角的和.
你能确定∠1与∠4的大小关系吗?
因为当∠4是锐角时,∠1>∠4;当∠4是直角时,∠1=∠4;当∠4是钝角时,∠1∠2,∠1>∠3.理由是什么?由前面我们知道∠1=∠2+∠3,所以∠1>∠2,∠1>∠3.由此你能得到什么结论?三角形的一个外角大于任何一个和它不相邻的内角.
在这里，我们通过三角形的内角和定理直接推导出两个新定理.像这样，由一个基本事实或定理直接推出的定理，叫做这个基本事实或定理的推论.推论可以当做定理使用.
解：∵∠2=∠1+∠B,∴∠2＞∠1.
解：∵∠2=∠1+∠B,∠3=∠2+∠D,∴∠3＞∠2＞∠1.
例1.已知：如图，在△ABC中，∠B=∠C，AD平分外角∠EAC.求证：AD//BC.
证明：∵∠EAC=∠B+∠C（三角形的一个外角 等于和它不相邻的两个内角的和）， ∠B=∠C（已知）， ∴∠C= ∵AD平分∠EAC（已知）， ∴∠DAC= ∴∠DAC=∠C（等量代换）. ∴AD//BC（内错角相等，两直线平行）.
证法二:推理可得:∠DAC=∠C (已证),∵∠BAC+∠B+∠C =180°(三角形内角和定理).∴∠BAC+∠B+∠DAC =180°(等量代换).∴AD∥BC(同旁内角互补,两直线平行).
这里是运用了定理“同旁内角互补,两直线平行”得到了证实.
例2.如图,P是△ABC内一点，连接PB，PC，∠B=∠C. 求证: ∠BPC＞∠A.
证明: 如图，延长BP，交AC于点D.∵∠BPC是△PDC的一个外角(外角定义),∴∠BPC>∠PDC(三角形的一个外角大于和它不相邻的任何一个内角).∵∠PDC是△ABD的一个外角(外角定义),∴∠PDC>∠A(三角形的一个外角大于和它不相邻的任何一个内角).∴ ∠BPC>∠A.（不等式的性质）
1.三角形外角的定义：三角形内角的一条边与另一条边的反向延长线组成的角．如图中的∠ACD的一条边是△ABC的边AC，另一条边是△ABC的边BC的延长线．
2.三角形的外角和等于360°.已知：∠1、∠2、∠3为△ABC的三个外角，如图．求证：∠1+∠2+∠3=360°．证明：∵∠1+∠BAC=180°， ∠2+∠BCA=180°，∠3+∠ABC=180°， ∴∠1+∠2+∠3+（∠BAC+∠BCA+∠ABC）=540° （等式性质）. ∵∠BAC+∠BCA+∠ABC=180°（三角形内角和定理）， ∴∠1+∠2+∠3=360°.
1.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( )A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法确定
2.如图，在△ABC中，∠B＝40°，∠C＝ 30°，延长BA至点D，则∠CAD的大小为(　　)A．110° B．80° C．70° D．60°
3.如图，△ABC中，∠A＝40°，点D为AB延长线上一点，且∠CBD＝120°，则∠C等于(　　)A．40° B．60° C．80° D．100°
4 .如图，D是△ABC的BC边上一点,∠B=∠BAD, ∠ADC=80°，∠BAC=70°，求：（1）∠B 的度数；（2）∠C的度数.