初中5 三角形的内角和定理教学ppt课件

这是一份初中5 三角形的内角和定理教学ppt课件，共21页。PPT课件主要包含了知识回顾，三角形的外角的概念，三角形的外角的性质，∠1∠A+∠B，∠1与∠2互补，三角形的外角，三角形的外角和等内容，欢迎下载使用。

1.了解并掌握三角形的外角的定义．2.掌握三角形的外角的性质，利用外角的性质进行简单的证明和计算．
7.5 三角形内角和定理 （第2课时）
三角形内角和定理：三角形三个内角的和等于180°.
在一个三角形花坛的外围走一圈，在每一个拐弯的地方都转了一个角度（∠1，∠2，∠3），那么回到原来位置时（方向与出发时相同），一共转了多少度？
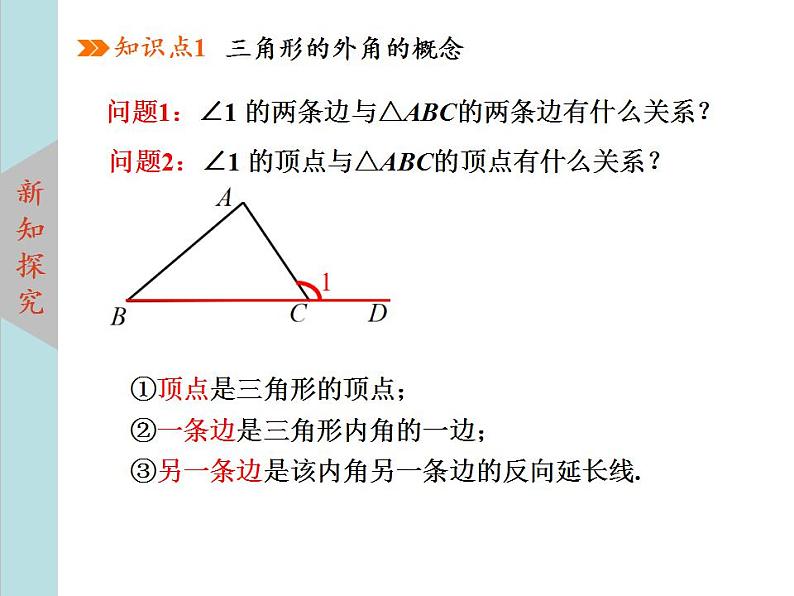
问题1：∠1 的两条边与△ABC的两条边有什么关系？
问题2：∠1 的顶点与△ABC的顶点有什么关系？
①顶点是三角形的顶点；②一条边是三角形内角的一边；③另一条边是该内角另一条边的反向延长线.
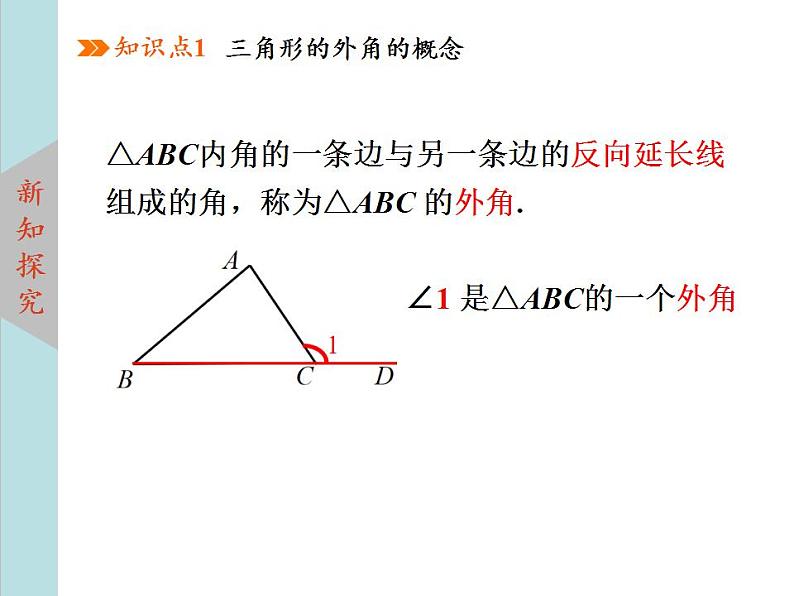
△ABC内角的一条边与另一条边的反向延长线组成的角，称为△ABC 的外角.
∠1 是△ABC的一个外角
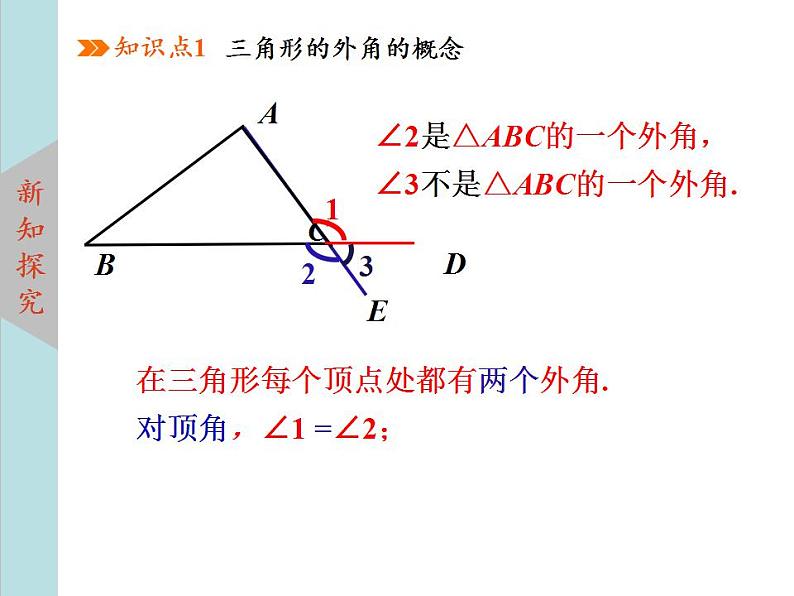
在三角形每个顶点处都有两个外角.对顶角，∠1 =∠2；
∠2是△ABC的一个外角，∠3不是△ABC的一个外角.
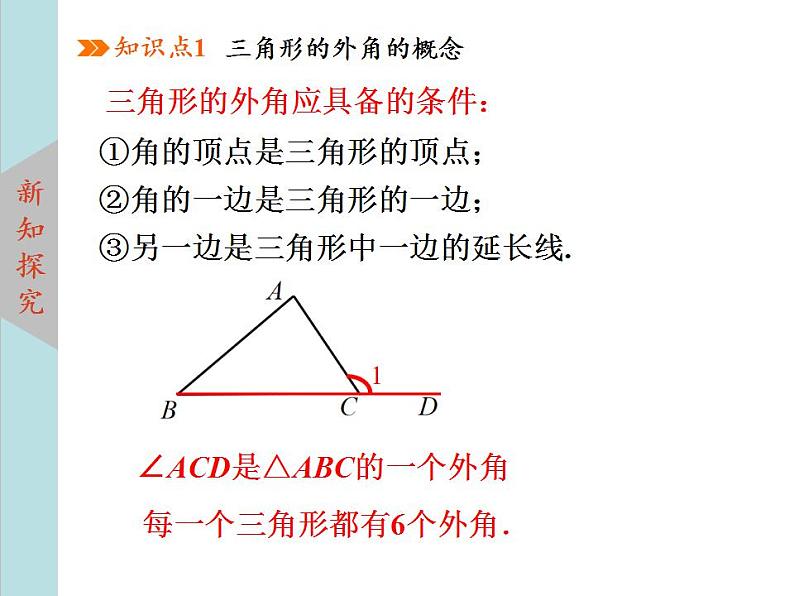
三角形的外角应具备的条件：
①角的顶点是三角形的顶点；②角的一边是三角形的一边；③另一边是三角形中一边的延长线.
∠ACD是△ABC的一个外角
每一个三角形都有6个外角．
例1.如图,∠ BEC是哪个三角形的外角？∠AEC是哪个三角形的外角？∠EFD是哪两个三角形的外角？ 　
解：∠BEC是△AEC的外角;
∠AEC是△BEC的外角;
∠EFD是△BEF和△DCF的外角.
问题：∠1 与△ABC的三个内角之间有什么关系？
∠1+∠2=180°(平角的定义).
∠1 ＞ ∠A ， ∠1＞ ∠B
定理：三角形的一个外角大于任何一个与它不相邻的内角.
三角形内角和定理有关外角的两个推论：
∵ ∠1 是△ABC 的外角∴ ∠1=∠B+∠C
∵ ∠1 是△ABC 的外角∴ ∠1 ＞ ∠B， ∠1＞ ∠C
定理：三角形的一个外角等于与它不相邻的两个内角的和.
例2. ①如图 ,试比较∠2 、∠1的大小； ②如图 ,试比较∠3 、∠2、 ∠1的大小.
解：∵∠2=∠1+∠B,∴∠2＞∠1.
∵∠2=∠1+∠B, ∠3=∠2+∠D,∴∠3＞∠2＞∠1.
例2. 如图,在△ABC中,AD平分外角∠EAC,∠B=∠C. 求证:AD∥BC.
证明: ∵ ∠EAC=∠B+∠C(三角形的一个外角等于和它不相邻的两个内角的和),
∴AD∥BC(内错角相等,两直线平行).
∠B=∠C (已知),
∴ ∠DAC=∠C(等量代换).
∵AD平分∠EAC(已知)，
例3. 已知:如图，P是△ABC内一点，连接PB，PC. 求证:∠BPC>∠A.
∵ ∠BPC是△PDC的一个外角 (外角定义),
∴ ∠BPC>∠PDC (三角形的一个外角大于任意一个和它不相邻的内角).
∵ ∠PDC是△ABD的一个外角 (外角定义),
∴ ∠PDC>∠A (三角形的一个外角大于任意一个和它不相邻的内角).
∴ ∠BPC >∠A.
证明:如图，延长BP,交AC于点D.
1.
2.如图，在△ABC中， D是BC延长线上一点，∠B = 40°，∠ACD = 120°，则∠A等于( )A.60° B.70° C.80° D.90°
4.如图，直线a∥b,则∠ACB=_______.
5. 如图，∠A=51°，∠B=20°，∠C=30°，求∠BDC的度数.
解：连接AD并延长于点E.在△ABD中，∠1+∠ABD=∠3，在△ACD中，∠2+∠ACD=∠4.∵∠BDC=∠3+∠4，∠BAC=∠1+∠2，∴∠BDC=∠BAC+∠ABD+∠ACD =51°+20°+30°=101°.
角一边必须是三角形的一边，另一边必须是三角形另一边的延长线
1.三角形的外角等于与它不相邻的两个内角的和
三角形的外角和等于360 °
2.三角形的外角大于与它不相邻的任何一个内角