八年级上册5 三角形的内角和定理教课课件ppt

这是一份八年级上册5 三角形的内角和定理教课课件ppt，共24页。PPT课件主要包含了画图并思考，今天的收获，小结2分钟等内容，欢迎下载使用。
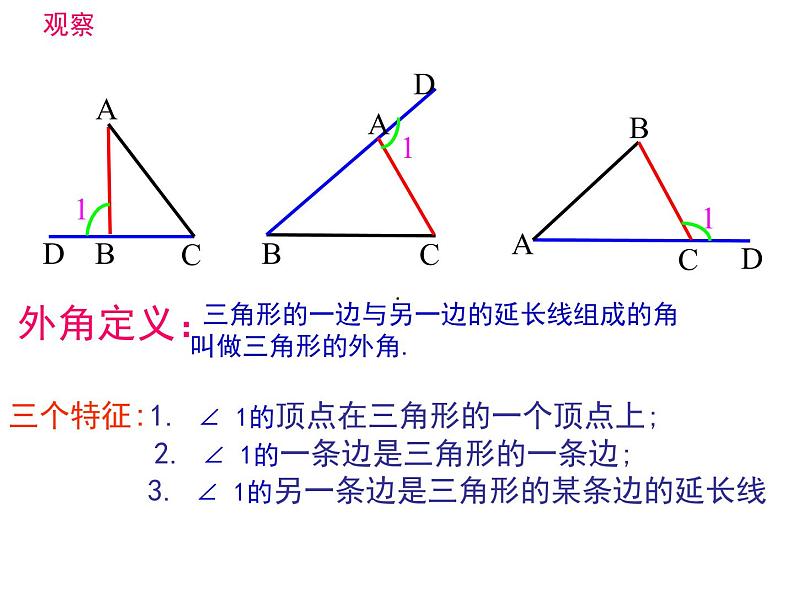
三角形的一边与另一边的延长线组成的角 叫做三角形的外角.
三个特征:1. ∠ 1的顶点在三角形的一个顶点上; 2. ∠ 1的一条边是三角形的一条边; 3. ∠ 1的另一条边是三角形的某条边的延长线
　画一个△ABC ，你能画出它的所有外角来吗？请动手试一试．同时想一想△ABC的外角共有几个呢？
　　每一个三角形都有６个外角．
每一个顶点相对应的外角都有２个．
每个外角与相邻的内角是邻补角．
1 2 4
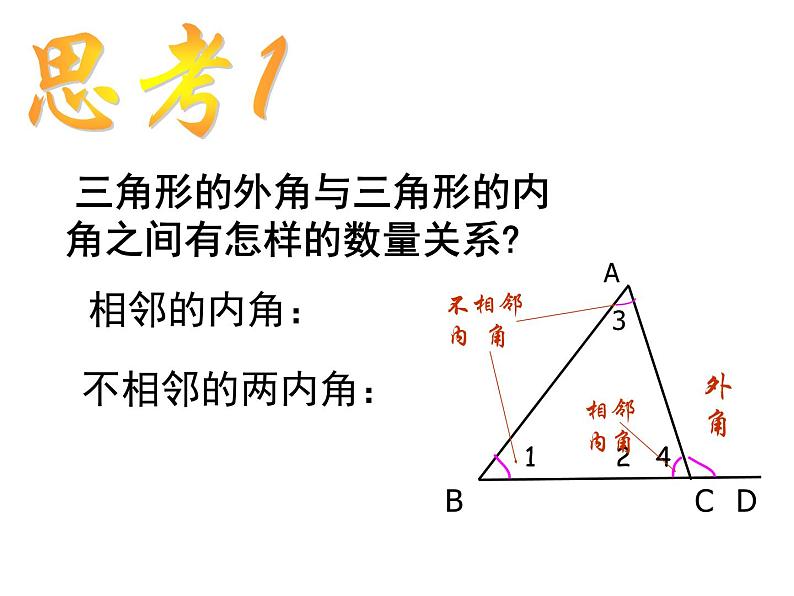
三角形的外角与三角形的内角之间有怎样的数量关系?
B C
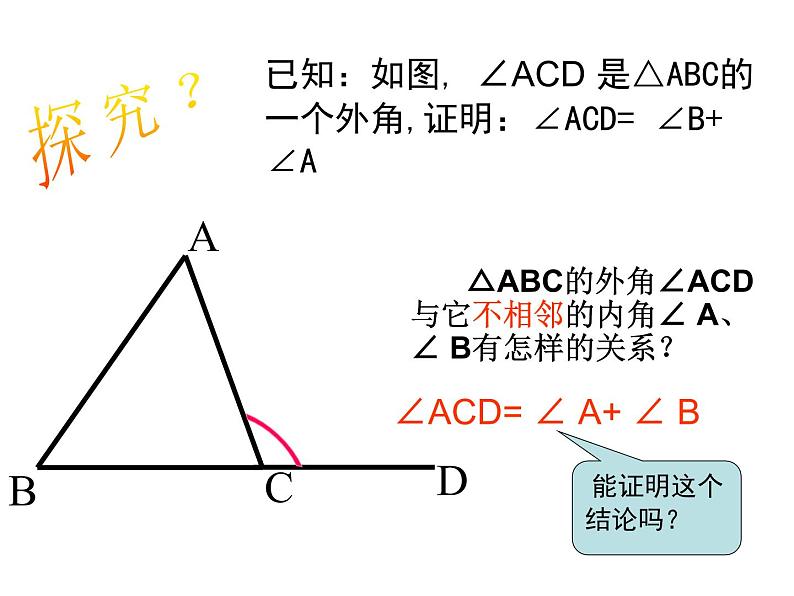
△ABC的外角∠ACD与它不相邻的内角∠ A、 ∠ B有怎样的关系？
∠ACD= ∠ A+ ∠ B
已知：如图, ∠ACD 是△ABC的一个外角,证明：∠ACD= ∠B+ ∠A
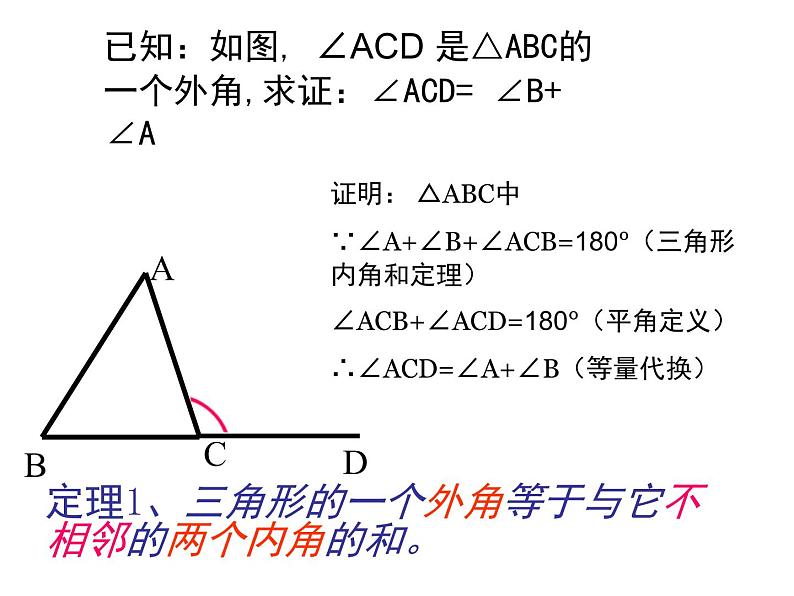
证明： △ABC中∵∠A+∠B+∠ACB=180°（三角形内角和定理）∠ACB+∠ACD=180°（平角定义）∴∠ACD=∠A+∠B（等量代换）
定理1、三角形的一个外角等于与它不相邻的两个内角的和。
已知：如图, ∠ACD 是△ABC的一个外角,求证：∠ACD= ∠B+ ∠A
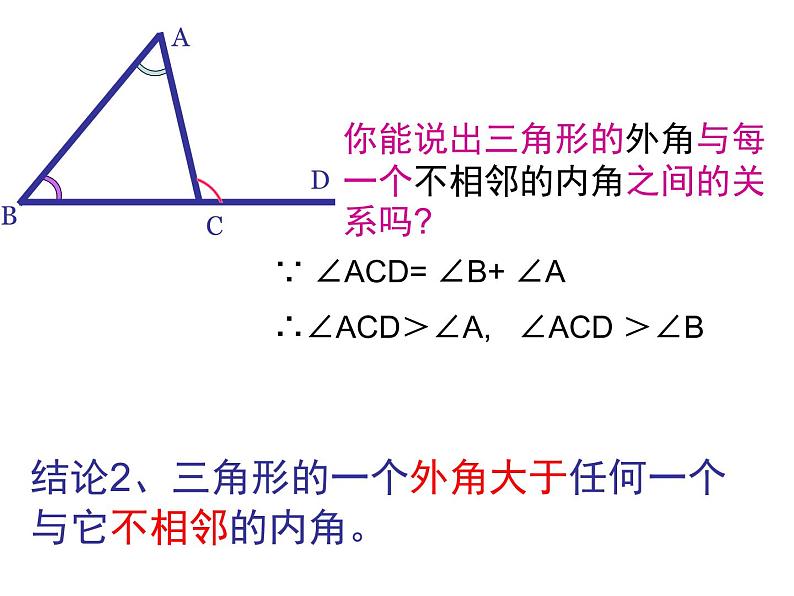
你能说出三角形的外角与每一个不相邻的内角之间的关系吗?
∵ ∠ACD= ∠B+ ∠A ∴∠ACD＞∠A, ∠ACD ＞∠B
结论2、三角形的一个外角大于任何一个与它不相邻的内角。
推论1：三角形的一个外角等于与它不相邻的两个内角的和。 推论2：三角形的一个外角大于与它不相邻的任何一个内角。
由公理、定理直接得出的真命题叫做推论。
证明：∵∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和) ∠B=∠C (已知)∴∠C= ∠EAC(等式性质)
例2 已知:如图，在△ABC中,AD平分外角∠EAC,∠B=∠C. 求证：AD∥BC.
∴∠DAC=∠C(等量代换)∴ AD∥BC(内错角相等,两直线平行).
∵ AD平分∠EAC(已知)∴∠DAC= ∠EAC(角平分线的定义)
例题是运用了定理“内错角相等,两直线平行”得到了证明.
证明：∵∠EAC=∠B+∠C (三角形的一个外角等于和它 不相邻的两个内角的和) ∠B=∠C (已知)∴∠B= ∠EAC(等式性质)
∵ AD平分∠EAC(已知)∴∠DAE= ∠EAC(角平分线的定义)
∴∠DAE=∠B(等量代换)∴ AD∥BC(同位角相等,两直线平行)
这里是运用了公理“同位角相等，两直线平行”得到了证明.
已知:如图在△ABC中,AD平分外角∠EAC,∠B=∠C. 求证：AD∥BC.
a、三角形的外角和是指三角形所有外角的和。（ ）b、三角形的外角和等于它内角和的2倍。（ ）c、三角形的一个外角等于两个内角的和。（ ）d、三角形的一个外角等于与它不相邻的两个内角的和。（ ）e、三角形的一个外角大于任何一个内角。（ ）f、三角形的一个内角小于任何一个与它不相邻的外角。（ ）
自学检测1（10分钟）
2、根据“三角形的一个外角等于和它不相邻的两个内角的和”可知： ∠1=∠ + ∠ . ∠2=∠ + ∠ . ∠3=∠ + ∠ . 三式相加得： ∠1+∠ 2+∠3 = 2（ ∠ + ∠ +∠ ） (1) 而 ∠4+∠5 + ∠6 = (2) 比较（1）与（2）可得：
∠1+∠ 2+ ∠3= 360º
3.如图:△ABC中，D是BC延长线上一点 1）则∠ ＞∠ ， ∠ ＞∠ ；
2）若∠A=35°,∠DCA=80°，则 ∠ACB= °∠B= °
4.如图，△ABC中，BD平分∠ABC，若∠A=85°，∠BDC=115°则∠ABC= °
学生自学，教师巡视（5分钟）
认真阅读P182内容，学习例题3，并思考：1、要证明两个角的不等关系，我们有哪些关于角的不等关系的结论？2、能直接运用这个结论吗？3、能否适当添加辅助线，构建出可以直接运用这个结论的角？4、你还有其他的证明方法吗？与同桌交流 注意解答过程和书写格式
例3：已知：如图P是△ABC内一点，连接PB、PC。（1）求证：∠BPC ＞ ∠BAC（2） ∠BPC 与∠BAC、 ∠ABP、 ∠ACP有怎样的数量关系？说明理由。
证明：法一：（1）延长BP交AC于点D. ∵ ∠BPC 是△PDC的一个外角 ∴ ∠BPC＞ ∠PDC ∵ ∠PDC是△ABD的一个外角 ∴ ∠PDC ＞ ∠BAC ∴ ∠BPC ＞ ∠BAC
法二：连接AP并延长交BC于点E.
∵ ∠1是△ABP的一个外角 ∴ ∠1 ＞ ∠3 ∵ ∠2是△ACP的一个外角 ∴ ∠2 ＞ ∠4 ∴ ∠ 1+ ∠2 ＞ ∠3+ ∠4 即 ∠BPC ＞ ∠BAC
(2)证明：（法一） ∵ ∠1 是△ABP的一个外角∴ ∠1=∠3+ ∠ 5∵ ∠2是△ACP的一个外角∴ ∠2 = ∠4+ ∠6∴ ∠ 1+ ∠2= ∠3+ ∠ 4+ ∠5+ ∠6即 ∠BPC = ∠BAC + ∠ ABP + ∠ACP
（法二）∠BPC = ∠A+ ∠ABP+ ∠ACP证明：∵ ∠1 是△PDC的一个外角 ∴ ∠1 = ∠2+ ∠3 ∵ ∠2是△ABD的一个外角 ∴ ∠2=∠A+ ∠4 ∴ ∠1 = ∠A+ ∠3+ ∠4 即∠BPC = ∠A+ ∠ABP+ ∠ACP
自学检测2（10分钟）
1.已知：如图所示,在△ABC中,∠A=45°，∠B=550 ∠ACB= .
2.已知：如图所示.求证：(1)∠BDC>∠A (2)∠BDC=∠A+∠B+∠C.
证明(1) ：延长ＢD交ＡＣ于Ｅ ∵∠BDC是△DEC的一个外角 ∴∠BDC>∠DEC (三角形的一个外角大 于任何一个和它不相邻的内角)∵∠DEC是△ABE的一个外角∴∠DEC>∠A(三角形的一个外角大于 任何一个和它不相邻的内角)∴∠BDC>∠A
2.已知：如图所示.求证：(1)∠BDC>∠A; (2)∠BDC=∠A+∠B+∠C.
证明：(2)∵∠BDC是△DEC的一个外角 ∴∠BDC =∠C+∠DEC (三角形的一个外角等于和它不相邻的两个内角的和) ∵∠DEC是△ABE的一个外角 ∴∠DEC=∠A+∠B (三角形的一个外角等于和它不相邻的两个内角的和) ∴∠BDC=∠A+∠B+∠C (等量代换)
1 三角形的外角性质：
三角形的一个外角等于与它不相邻的两个内角的和；
三角形的一个外角大于任何一个与它不相邻的内角。
2 三角形的内角和等于180˚
1、求下列各图中∠1的度数。
2、如图，已知AB∥CD，∠A＝50°， ∠C＝∠E．则∠C＝（ ） A．20° B．25° C．30° D．40°
已知：在△ABC中, ∠1是它的一个外角, E为边AC上一点,延长BC到D,连接DE. 求证: ∠1>∠2.
2.已知：如右下图在△ABC中，AD⊥BC于D，AE平分∠BAC(∠C >∠B)，求证：∠EAD= (∠C-∠B)
1、如左下图：是一个五角星， 求证∠A +∠B +∠C +∠D +∠E =180°
4 已知：在△ABC中, ∠1是它的一个外角, E为边AC上一点,延长BC到D,连接DE.求证: ∠1>∠2.
证明：∵ ∠1是△ABC的外角 (已知)∴ ∠1>∠3 (三角形的一个外角大于任何一个和它不相 邻的内角)∵∠3是△CDE的一个外角 ∴∠3>∠2 (三角形的一个外角大于任何一个和它不相 邻的内角)∴ ∠1>∠2
证明:∵∠1是△BDF的一个外角(外角的定义),
∴ ∠1=∠B+∠D(三角形的一个外角等于和它不相邻的两个内角的和).
∴ ∠2=∠C+∠E(三角形的一个外角等于和它不相邻的两个内角的和).
又∵∠A+∠1+∠2=180°(三角形内角和定理).
又∵ ∠2是△EHC的一个外角(外角的定义),
∴ ∠A+∠B+∠C+∠D+∠E =180°
1.如图1：是一个五角星，求证:∠A+∠B+∠C+∠D+∠E=180°