苏科版（2024）九年级上册2.7 弧长及扇形的面积精品课件ppt

这是一份苏科版（2024）九年级上册2.7 弧长及扇形的面积精品课件ppt，共31页。PPT课件主要包含了学习目标，圆的周长C2πR，知识回顾，圆的面积SπR2，扇面是圆面的一部分，将圆周分成360等份，思考与探索，弧长公式，新知归纳，圆心角等内容，欢迎下载使用。
2.会运用弧长计算公式、扇形面积的计算公式计算有关问题.
1.理解弧长和扇形面积公式；
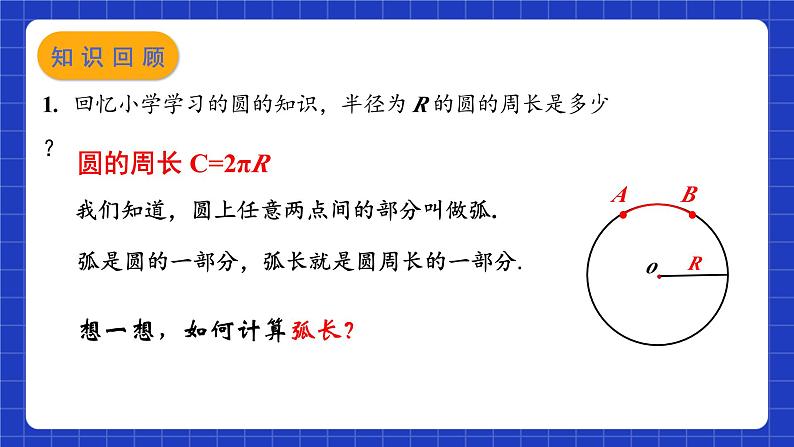
1. 回忆小学学习的圆的知识，半径为 R 的圆的周长是多少？
我们知道，圆上任意两点间的部分叫做弧.
想一想，如何计算弧长？
弧是圆的一部分，弧长就是圆周长的一部分.
2. 回忆小学学习的圆的知识，半径为 R 的圆的面积是多少？
我们知道，一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形.
想一想，如何计算扇形的面积？
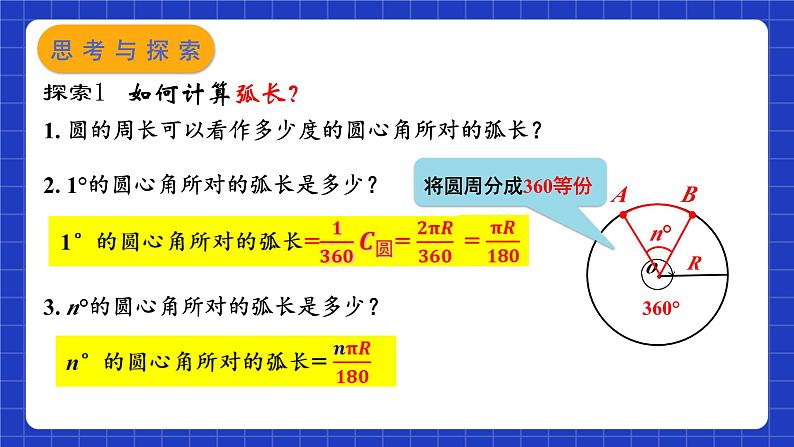
探索1 如何计算弧长？
1. 圆的周长可以看作多少度的圆心角所对的弧长？
2. 1°的圆心角所对的弧长是多少？
3. n°的圆心角所对的弧长是多少？
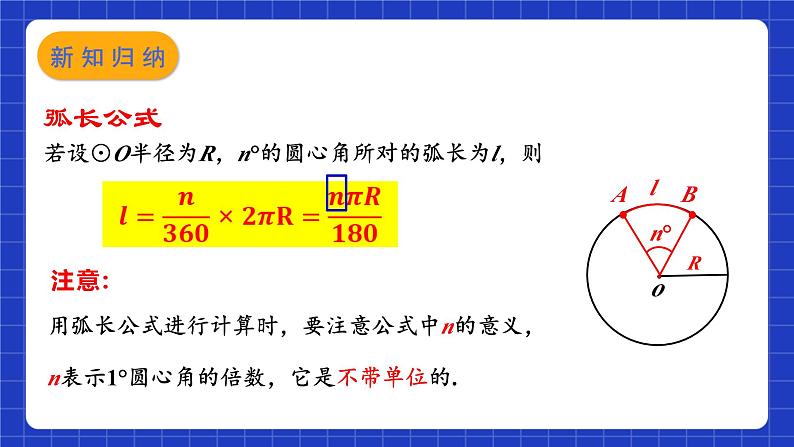
若设⊙O半径为R，n°的圆心角所对的弧长为l，则
用弧长公式进行计算时，要注意公式中n的意义，n表示1°圆心角的倍数，它是不带单位的.
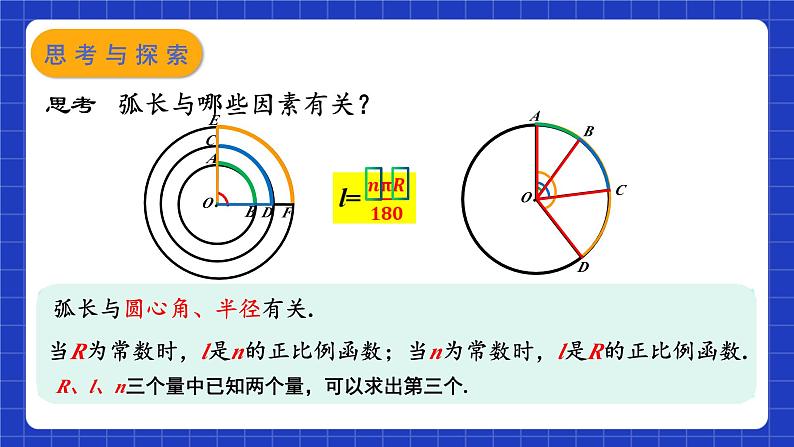
思考 弧长与哪些因素有关？
________大小不变时，对应的弧长大小与______有关，_____越大，弧长越大.
圆的 不变时，对应的弧长大小与_______有关，_______越大，弧长越大.
弧长与圆心角、半径有关.
当R为常数时，l是n的正比例函数；当n为常数时，l是R的正比例函数.
R、l、n三个量中已知两个量，可以求出第三个.
1.已知圆的半径为4 ，90°圆心角所对的弧长为 .2.已知半径为3，则弧长为π的弧所对的圆心角为_______ . 3.已知圆心角为150°，所对的弧长为20π，则圆的半径为______.
探索2 类比弧长公式推导过程自主推导扇形的面积的计算公式.
1. 1°的圆心角所对的扇形面积是多少？
2. n°的圆心角所对的扇形面积是多少？
若设⊙O半径为R，圆心角为n°的扇形的面积S扇形，则
用扇形面积公式进行计算时，要注意公式中n的意义，n表示1°圆心角的倍数，它是不带单位的.
思考 扇形的面积与哪些因素有关？
_________大小不变时，对应的扇形面积与 ______有关，_____越大，扇形面积越大.
圆的______不变时，对应的扇形面积与_______有关，_______越大，扇形面积越大.
扇形的面积与圆心角、半径有关.
比较扇形面积公式与弧长公式，找出它们之间的联系？
2.扇形的圆心角为60°，半径为6cm，则这个扇形的弧长为_______， 这个扇形的面积为_________.
1.一个扇形的弧长为20πcm，半径为24cm，则该扇形的面积为_________.
3.已知扇形的圆心角为120°,弧长为20π，扇形的面积为 ．
例1 如图，△ABC是⊙O的内接三角形，∠BAC＝60°．设⊙O的半径为2.(2)求图中阴影部分的面积．
例2 如图，折扇打开后，OA、OB的夹角为120°，OA的长为30cm，AC的长为20cm，求图中纸面部分的面积S．
不规则图形面积的求法： 求圆中不规则图形的面积的基本思想是转化思想，一般思路是通过添加辅助线，将要求的不规则图形的面积转化为规则图形(三角形、扇形等)的面积的和或差，进而求解．
不规则图形的面积的求法：转化为规则图形的面积的和或差
A．π－2 　　　 B．π－4 C．4π－2 　　 D．4π－4
3.如图，已知扇形AOB的半径为2，圆心角为90°，连接AB，则图中阴影部分的面积是 (　　)
4.如图，在同心圆中，大圆半径OA、OB交小圆于C、D，且OC∶OA=1∶2，则弧CD与弧AB长度之比为( )
A.1∶1 B.1∶2 C.2∶1 D.1∶4
5.如图，⊙A、 ⊙B、 ⊙C、⊙D两两不相交，且半径都是2cm，则图中阴影部分的面积是________.
7.如图,扇形的圆心角为90°,半径OC=2，∠AOC=30°，CD⊥OB于点D，求阴影部分的面积.
8.如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm，求截面上有水部分的面积.(精确到0.01cm).
讨论：1.截面上有水部分的面积是指图上哪一部分？
弓形的面积 = S扇形OAB- S△OAB
变式：如图、水平放置的圆柱形排水管道的截面半径是0.6cm，其中水面高0.9cm，求截面上有水部分的面积.
弓形的面积 = S扇形OAB+ S△OAB
弓形的面积=扇形的面积±三角形的面积
9.如图，在△ABC中，∠ABC＝45°，AB＝AC，以AB为直径的☉O与边BC交于点D.
（1）判断直线AC与☉O的位置关系，并说明理由；
解：（1）直线AC与☉O相切　理由：∵∠ABC＝45°，AB＝AC，∴∠ABC＝∠C＝45°.∴在△ABC中，∠BAC＝180°－2×45°＝90°.∴BA⊥AC.∵AB是☉O的直径，∴直线AC与☉O相切.
（2）若AB＝4，求图中涂色部分的面积.