数学九年级上册2.8 圆锥的侧面积精品课件ppt

这是一份数学九年级上册2.8 圆锥的侧面积精品课件ppt，共33页。PPT课件主要包含了扇形+圆，圆锥的再认识，S侧πrl，全面积呢，∵S扇πrl，圆锥中的有关计算，分三种情况等内容，欢迎下载使用。
2.会运用圆锥的侧面积公式计算有关问题.
1.体会圆锥侧面积的探索过程，能够通过扇形面积公式推导圆锥侧面积公式；
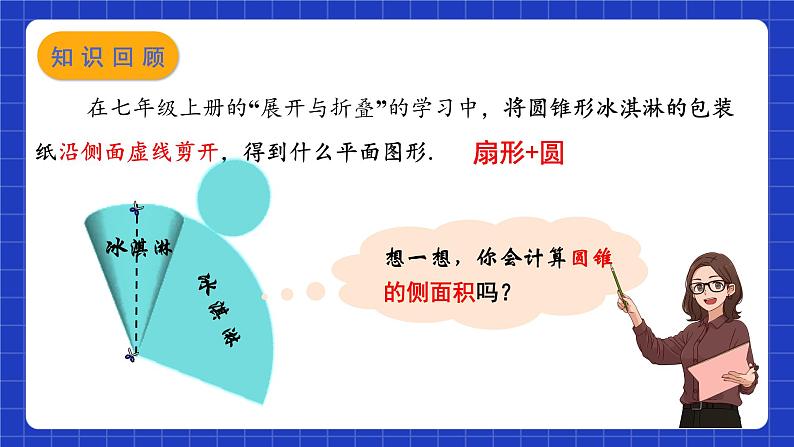
在七年级上册的“展开与折叠”的学习中，将圆锥形冰淇淋的包装纸沿侧面虚线剪开，得到什么平面图形.
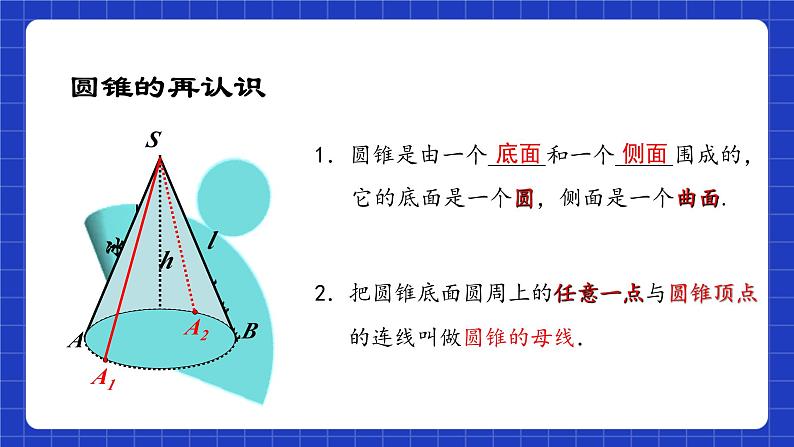
1．圆锥是由一个_____和一个_____围成的，
它的底面是一个圆，侧面是一个曲面.
2．把圆锥底面圆周上的任意一点与圆锥顶点 的连线叫做圆锥的母线．
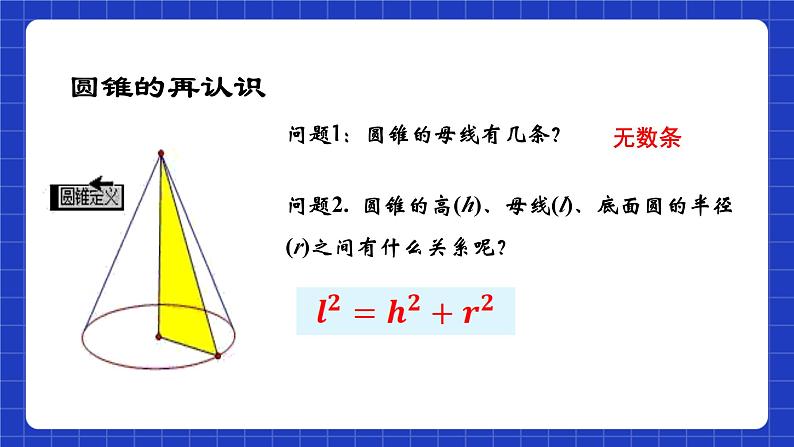
问题2. 圆锥的高(h)、母线(l)、底面圆的半径(r)之间有什么关系呢？
问题1：圆锥的母线有几条？
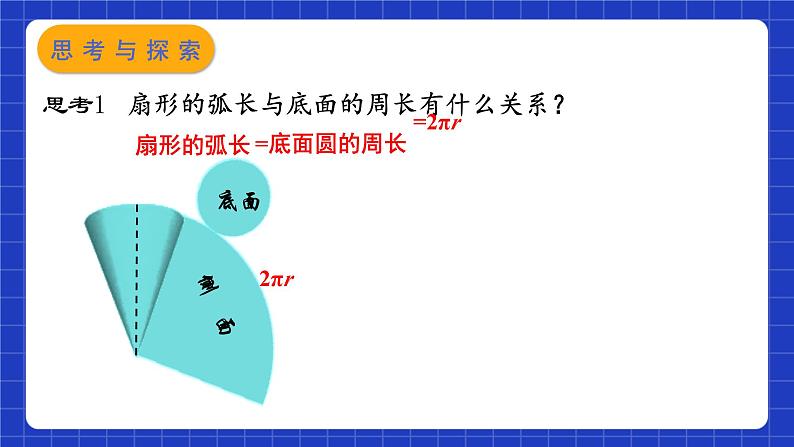
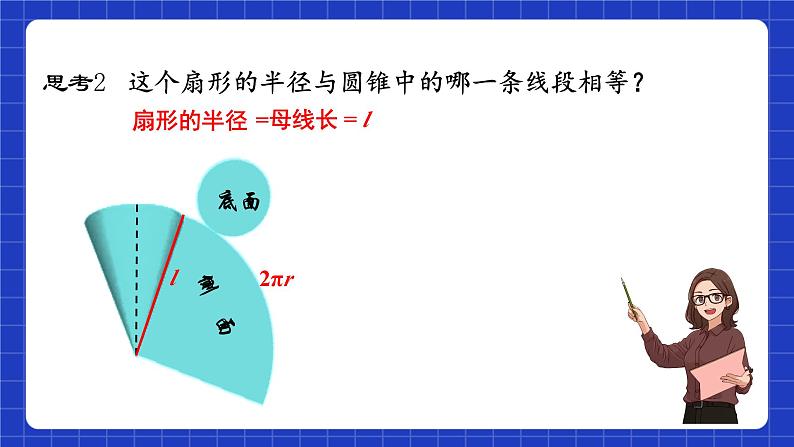
思考1 扇形的弧长与底面的周长有什么关系？
思考2 这个扇形的半径与圆锥中的哪一条线段相等？
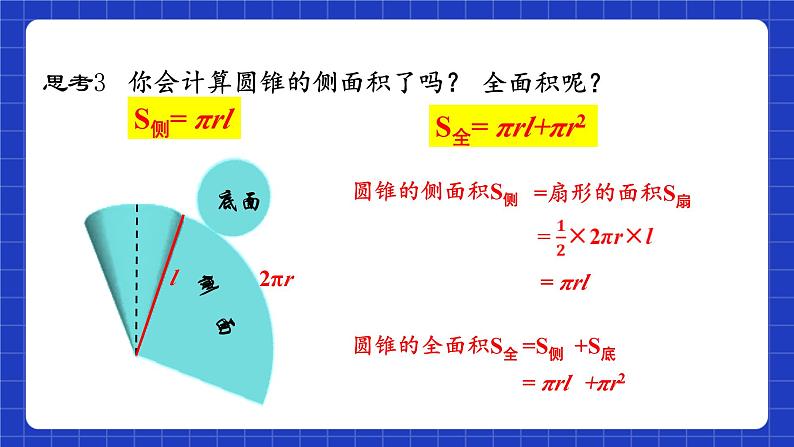
思考3 你会计算圆锥的侧面积了吗？
S全= πrl+πr2
思考4 侧面展开图中圆心角θ如何计算呢？
1.已知一个圆锥的底面半径为12，母线长为20，则这个圆锥的侧面积为______，全面积为_______.
S侧=πrl=π×12×20=240π
S全=πrl+πr2=240π+π×122=384π
2.已知圆锥的底面的半径为3，高为4，则它的侧面积是_____，全面积是_____．
3 .一个扇形，半径为3，圆心角为120°，用它做成一个圆锥的侧面，那么这个圆锥的底面半径为_____ ．
4. 若圆锥的底面半径r =4，高线h =3，则它的侧面展开图中扇形的圆心角是______度.
例1.用铁皮制作的圆锥形容器盖如图所示，求这个容器盖铁皮的面积（精确到1cm2 ）
例2.Rt△ABC中，∠C=90°，AC=3，BC=4，把它分别沿三边所在直线旋转一周，求所得几何体的表面积.
绕BC旋转：S全=S侧+S底 =πrl+πr2 =π×3×5+π×32 =24π.
绕AC旋转：S全=S侧+S底 =πrl+πr2 =π×4×5+π×42 =36π.
(2)用所剪的扇形纸片围成一个圆锥的侧面，求这个圆锥的底面圆半径；
(3)在被剪掉的3块余料中，能否从中选取一块剪出一个圆作为“(2)”中所围成的圆锥的底面？
∵r＞r’， ∴这样的圆不存在
1.圆锥的侧面积为384πcm2，其轴截面是一个等边三角形，则该轴截面的面积_______.
2.如图，已知Rt△ABC中，∠ACB=90°，AC= 4，BC=3，以AB边所在的直线为轴，将△ABC旋转一周，则所得几何体的表面积是_________.
3.圣诞节将近，某家商店正在制作圣诞节的圆锥形纸帽.已知纸帽的底面周长为30πcm，高为20cm，要制作20顶这样的纸帽至少要用多少纸?
4.如图，有一直径是1米的圆形铁皮，要从中剪出一个圆心角是120°的扇形ABC.(1)求被剪掉阴影部分的面积；(2)若用所留的扇形铁皮围成一个圆锥，则该圆锥底面圆的半径是多少？
解：(1)连接OA、OB、OC.
1. 已知圆锥的母线长是12，它的侧面展开图的圆心角是120°，则它的底面圆的直径为(　　)A．2 B．4 C．6 D．8
2.圆锥的侧面展开图是一个弧长为12π的扇形，则这个圆锥底面圆的半径是(　　)A．24 B．12 C．6 D．3
3.如图所示，圆锥形烟囱帽的底面半径为12 cm，侧面展开图为半圆形，则它的母线长为( )A.10 cmB.20 cmC.5 cmD.24 cm
4. 如图，用一张半径为24 cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计)，如果圆锥形帽子的底面半径为10 cm，那么这张扇形纸板的面积是(　　)A.240π cm2 B.480π cm2 C.1 200π cm2 D.2 400π cm2
S＝πrl＝π×10×24＝240π(cm2)
5.如图是一个圆锥形雪糕冰激凌外壳（不计厚度），已知其母线长为12cm，底面圆半径为3cm.则这个冰激凌外壳的侧面积等于________.（结果保留π）
6.如图，若圆锥的侧面展开图是半圆，那么这个展开图的圆心角是_____度；圆锥底半径 r与母线l的比r ：l = ______.
7.如图，从一块直径是8 m的圆形铁皮上剪出一个圆心角为90°的扇形，将剪下的扇形围成一个圆锥，圆锥的高是______m.
8.如图，要造一个粮仓，其上部是圆锥，下部是圆柱.如果每平方米需用铁皮2m2（底部不用铁皮，接头处忽略不计），那么按图中尺寸计算，共需多少平方米铁皮（精确到0.1m2）？
1. 设圆锥的底面圆半径为r，圆锥的母线长为l，满足2r＋l＝6，这样的圆锥的侧面积( )
2.如图，有一个圆锥形的粮堆，其轴截面是边长为6m的等边三角形，在圆锥的母线AC的中点P处有一只老鼠正在偷吃粮食，此时小猫正在点B处，它要沿圆锥侧面到达点P处捕捉老鼠.求小猫所经过的最短路径？