（安徽卷）中考数学第三次模拟考试（2份，原卷版+解析版）

这是一份（安徽卷）中考数学第三次模拟考试（2份，原卷版+解析版），文件包含安徽卷中考数学第三次模拟考试全解全析doc、安徽卷中考数学第三次模拟考试考试版doc等2份试卷配套教学资源，其中试卷共25页， 欢迎下载使用。
（考试时间：120分钟 试卷满分：150分）
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。写在本试卷上无效。
3．回答第Ⅱ卷时，将答案写在答题卡上。写在本试卷上无效。
4．考试结束后，将本试卷和答题卡一并交回。
5．考试范围：中考全部内容。
第Ⅰ卷
一、选择题（本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的）
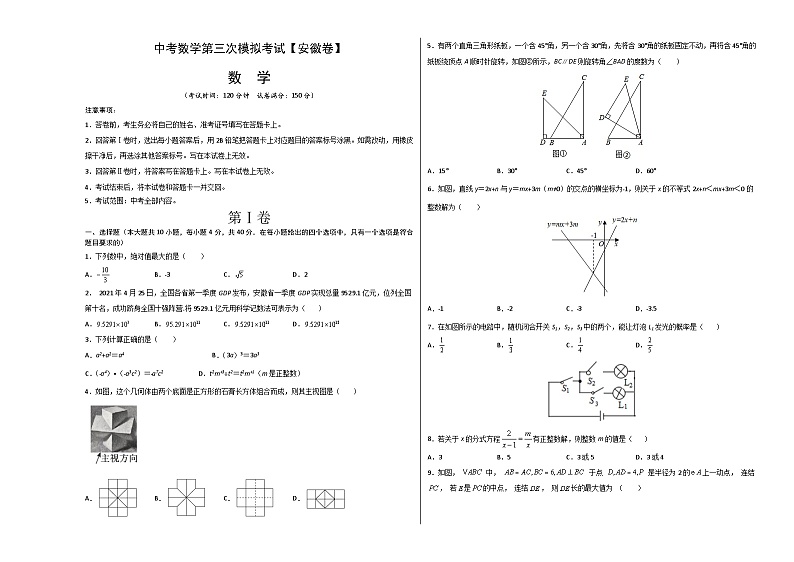
1．下列数中，绝对值最大的是（ ）
A．B．﹣3C．D．2
2． 2021年4月25日，全国各省第一季度GDP发布，安徽省一季度GDP实现总量9529.1亿元，位列全国第十名，成功跻身全国十强阵营.将9529.1亿元用科学记数法可表示为（ ）
A．B．C．D．
3．下列计算正确的是（ ）
A．a2+a2＝a4 B．（3a）3＝3a3
C．（﹣a4）•（﹣a3c2）＝﹣a7c2 D．t2m+3÷t2＝t2m+1（m是正整数）
4．如图，这个几何体由两个底面是正方形的石膏长方体组合而成，则其主视图是（ ）
A．B．C．D．
5．有两个直角三角形纸板，一个含45°角，另一个含30°角，先将含30°角的纸板固定不动，再将含45°角的纸板绕顶点A顺时针旋转，如图②所示，BC∥DE则旋转角∠BAD的度数为（ ）
A．15°B．30°C．45°D．60°
6．如图，直线y＝2x+n与y＝mx+3m（m≠0）的交点的横坐标为﹣1，则关于x的不等式2x+n＜mx+3m＜0的整数解为（ ）
A．﹣1B．﹣2C．﹣3D．﹣3.5
7．在如图所示的电路中，随机闭合开关S1，S2，S3中的两个，能让灯泡L1发光的概率是（ ）
A．B．C．D．
8．若关于x的分式方程有正整数解，则整数m的值是（ ）
A．3B．5C．3或5D．3或4
9．如图， 中， 于点 是半径为2的上一动点， 连结 ， 若是的中点， 连结， 则长的最大值为 （ ）
A．3B．C．4D．
10．如图，在正方形ABCD中，F是BC边上一点，连接AF，以AF为斜边作等腰直角三角形AEF．有下列四个结论：①∠CAF＝∠DAE；②；③当∠AEC＝135°时，E为△ADC的内心；④若点F在BC上以一定的速度，从B往C运动，则点E与点F的运动速度相等．其中正确的结论的个数为（ ）
A．1B．2C．3D．4
第Ⅱ卷
二、填空题（本大题共4小题，每小题5分，共20分）
11．幻方是相当古老的数学问题，我国古代的《洛书》中记载了最早的幻方---九宫图．将数字1~9分别填入如图所示的幻方中，要求每一横行、每一竖行以及两条斜对角线上的数字之和都是15，则的值为______．
12．商家通常依据“乐观系数准则”确定商品的销售价格，即根据商品的最低销售限价，最高销售限价以及实数确定实际销售价格，这里的被称为乐观系数．经验表明，最佳乐观系数恰好使得，据此可得，最佳乐观系数的值等于__________．
13．在菱形中，，，，相交于点．将一个足够大的直角三角板60°角的顶点放在菱形的顶点处，绕点左右旋转，其中三角板60°角的两边分别与边，相交于点，，连接与相交于点．旋转过程中，当点为边的四等分点时（），______．

14．（2022·安徽舒城·九年级期末）如图，抛物线y=-x+2x+c交x轴于点A（-1，0）、B（3，0），交y轴于点C，D为抛物线的顶点．（1）点D坐标为_____；（2）点C关于抛物线对称轴的对称点为E点，点M是抛物线对称轴上一点，且△DMB和△BCE相似，点M坐标为_____．
三、解答题（本大题共8小题，共90分．其中：15-18题，每题8分，19-20题，每题10分，21-22题，每题12分，23题14分，解答应写出文字说明、证明过程或演算步骤）。
15．（1）计算：；
（2）解不等式组：并求出它的整数解．
16．如图，△ABC三个顶点的坐标分别为A（1，1），B（4.2）．C（3.4）
（1）请画出将△ABC向左平移6个单位长度后得到的图形△A1B1C1；
（2）请画出△ABC绕原点O顺时针旋转90°的图形△A2B2C2；
（3）△A2B2C2可看成将△A1B1C1以某点为旋转中心旋转而得，则旋转中心的坐标是 ．
17．为了提高学生应用数学方法解决实际问题的能力，老师组织全班同学开展了测量物体高度的实践活动．小明所在的小组为测量学校教学楼的高度经讨论之后，他们准备以学校的旗杆为参照物进行测量，教学楼和旗杆底部均不可到达．如图，教学楼AB与旗杆CD的底部B，D在同一平面上，经查阅有关资料得知教学楼和旗杆之间的距离BD长为70米，旗杆CD高度为11.5米．经过分析，他们设计了以下测量方案：小明站在MN处，标杆立在EF处，点B、N、F、D共线，此时小明的眼睛M点、标杆的顶部E点和旗杆的顶部C点在一条直线上，然后，小明原地转身180°后，利用自制的测倾器测得教学楼的顶部A的仰角为40°．已知：AB⊥BD，MN⊥BD，EF⊥BD，CD⊥BD，测得MN＝1.5米，EF＝2米，FN＝2米，利用以上测量数据求教学楼AB的高度．（参考数据：sin40°≈0.64，cs40°≈0.77，tan40°≈0.84）
18．实际问题：某学校共有18个教学班（每班的学生都多于10人）．为了解学生课余时间上网情况，学校打算做一次抽样调查，如果要确保全校抽取出来的学生中至少有10人在同一班级，那么全校最少需抽取多少名学生？
建立模型：为解决上面的“实际问题”，我们先建立并研究下面从口袋中摸球的数学模型：在不透明的口袋中装有红、黄、白、……m种颜色的小球若干个（除颜色外完全相同），现要确保从口袋中随机模出的小球至少有n个是同色的，则最少需摸出多少个小球？
为了找到解决问题的办法，我们可把上述问题简单化．
探究一：我们研究一个口袋中装有红、黄、白3种颜色的小球若干个（除颜色外完全相同），现要确保从口袋中随机摸出的小球至少有n个是同色的，则最少需摸出多少个小球？
（1）我们首先考虑最简单的情况：即要确保从装有红、黄、白3种颜色的口袋中摸出小球，至少有2个是同色的，则最少需摸出多少个小球？
假若从袋中随机摸出3个小球，它们的颜色可能会出现多种情况，其中最不利的情况就是它们的颜色各不相同，那么只需再从发中摸出1个小球就可确保至少有2个小球同色，即最少需摸出小球的个数是：1+3=4（如图①）；
（2）要确保从装有红、黄、白3种颜色的口袋中摸出小球，至少有3个是同色的，则最少需摸出多少个小球？我们只需在（1）的基础上，再从袋中摸出3个小球，就可确保至少有3个小球同色，即最少．需摸出小球的个数是：1+3×2=7（如图②）
（3）要确保从装有红、黄、白3种颜色的口袋中摸出小球，至少有4个是同色的，则最少需摸出多少个小球？我们只需在（2）的基础上，再从袋中摸出3个小球，就可确保至少有4个小球同色，即最少需摸出小球的个数是：1+3×3=10（如图③）；……
（4）要确保从装有红、黄、白3种颜色的口袋中摸出小球，至少有10个是同色的，则最少需摸出多少个小球？最少需摸出小球的个数是________；
（5）要确保从装有红、黄、白3种颜色的口袋中摸出小球，至少有n个是同色的，则最少需摸出 个小球．
探究二：我们研究一个口袋中装有红、黄、白黑4种颜色的小球若干个（除颜色外完全相同），现要确保从口袋中随机摸出的小球至少有n个是同色的，则最少需摸出多少个小球？
（6）我们首先考虑最简单的情况：即要确保从装有红、黄、白、黑4种颜色的口袋中摸出小球，至少有2个是同色的，则最少需摸出______个小球；
（7）要确保从装有红、黄、白、黑4种颜色的口袋中摸出小球，至少有3个是同色的，则最少需摸出______个小球；
（8）要确保从装有红、黄、白黑4种颜色的口袋中摸出小球，至少有4个是同色的，则最少需摸出_____个小球；
（9）要确保从装有红、黄、白、黑4种颜色的口袋中摸出小球，至少有n个是同色的，则最少需摸出_____个小球；
探究三：在不透明的口袋中装有红、黄、白、蓝、绿5种颜色的小球若干个（除颜色外完全相同），现从袋中随机摸球：若要确保摸出的小球至少有n个同色，则最少需摸出小球的个数是______．
探究四：在不透明口袋中装有m种颜色的小球若干个（除颜色外完全相同），现从袋中随机摸球：若要确保摸出的小球至少有n个同色，则最少需摸出小球的个数是________；
问题解决：根据上述探究过程中建立的数学模型，求出全校最少需抽取名学生．
19．如图，直线y＝x，与反比例函数在第一象限内的图象相交于点A(4，m)． (1)求该反比例函数的表达式；(2)将直线y＝x沿y轴向上平移n个单位后与反比例函数在第一象队内的图象相交于点B，与y轴交于点C，若，求n的值．(3)在（2）的条件下，连接AB，在x轴上有一点P，使△ABP为等腰三角形，直接写出点P的坐标．
20．如图，在Rt△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，O为AB上一点，经过点A，D的圆O分别交AB，AC于点E，F，连接EF．
(1)求证：BC是圆O的切线；(2)求证：AD2＝AF•AB；(3)若BE＝16，sinB，求AD的长．
21．某校为了进一步宣传垃圾分类相关知识，举办了全体1200名学生参加的垃圾分类知识竞赛，并随机抽取了参加竞赛的40名选手的成绩（满分100分，得分为正整数且无满分，最低75分），将抽出的成绩分成五组，绘制了不完整的统计图表．
(1)表中m＝_____，n＝_____；(2)请在图中补全频数分布直方图；(3)小明同学的成绩被抽取到了，且他的成绩是40位参赛选手成绩的中位数，则他的成绩落在的分数段为_____；(4)请你估计全校成绩为优秀（90分及以上）的学生人数．
22．如图，已知抛物线y=ax2+bx-4与x轴交于A，B两点，与y轴交于点C，且点A的坐标为（-2，0），直线BC的解析式为y=x-4． (1)求抛物线的解析式；(2)如图1，过点A作AD∥BC交抛物线于点D（异于点A），P是直线BC下方抛物线上一点，过点P作PQ∥y轴，交AD于点Q，过点Q作QR⊥BC于点R，连接PR．求△PQR面积的最大值及此时点P的坐标； (3)如图2，点C关于x轴的对称点为点C′，将抛物线沿射线C′A的方向平移2个单位长度得到新的抛物线y′，新抛物线y′与原抛物线交于点M，原抛物线的对称轴上有一动点N，平面直角坐标系内是否存在一点K，使得以D，M，N，K为顶点的四边形是矩形？若存在，请直接写出点K的坐标；若不存在，请说明理由．

23．在△ABC中，P是BC边上的一动点，连接AP．
图1 图2 图3
(1)如图1，，，且．求：△ABP的面积．
(2)如图2，若，以AP为边作等腰Rt△APE，连接BE，F是BE的中点，连接AF，猜想PE，PB，AF之间有何数量关系？并证明你的结论．(3)如图3，作于D，于E，若，，，当DE最小时，请直接写出DE的最小值．
分数段
频数
频率
74.5～79.5
2
0.05
79.5～84.5
m
0.2
84.5～89.5
12
0.3
89.5～94.5
14
n
94.5～99.5
4
0.1