（北京卷）中考数学第三次模拟考试（2份，原卷版+解析版）

这是一份（北京卷）中考数学第三次模拟考试（2份，原卷版+解析版），文件包含北京卷中考数学第三次模拟考试全解全析doc、北京卷中考数学第三次模拟考试考试版doc等2份试卷配套教学资源，其中试卷共26页， 欢迎下载使用。
第一部分 选择题
一、选择题(共16分，每题2分)。
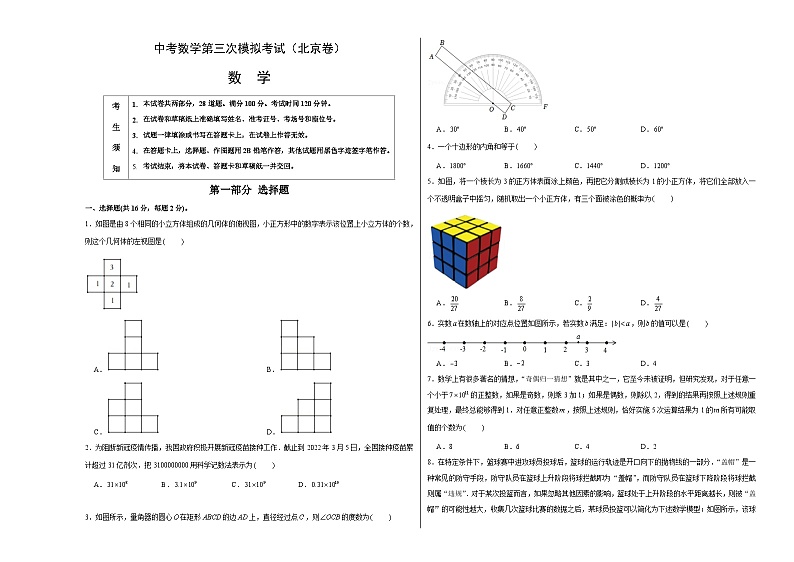
1．如图是由8个相同的小立方体组成的几何体的俯视图，小正方形中的数字表示该位置上小立方体的个数，则这个几何体的左视图是
A． B．
C． D．
2．为阻断新冠疫情传播，我国政府积极开展新冠疫苗接种工作．截止到2022年3月5日，全国接种疫苗累计超过31亿剂次．把3100000000用科学记数法表示为
A．B．C．D．
3．如图所示，量角器的圆心在矩形的边上，直径经过点，则的度数为
A．B．C．D．
4．一个十边形的内角和等于
A．B．C．D．
5．如图，将一个棱长为3的正方体表面涂上颜色，再把它分割成棱长为1的小正方体，将它们全部放入一个不透明盒子中摇匀，随机取出一个小正方体，有三个面被涂色的概率为
A．B．C．D．
6．实数在数轴上的对应点位置如图所示，若实数满足：，则的值可以是
A．B．C．3D．4
7．数学上有很多著名的猜想，“奇偶归一猜想”就是其中之一，它至今未被证明，但研究发现，对于任意一个小于的正整数，如果是奇数，则乘3加1；如果是偶数，则除以2，得到的结果再按照上述规则重复处理，最终总能够得到1．对任意正整数，按照上述规则，恰好实施5次运算结果为1的所有可能取值的个数为
A．8B．6C．4D．2
8．在特定条件下，篮球赛中进攻球员投球后，篮球的运行轨迹是开口向下的抛物线的一部分．“盖帽”是一种常见的防守手段，防守队员在篮球上升阶段将球拦截即为“盖帽”，而防守队员在篮球下降阶段将球拦截则属“违规”．对于某次投篮而言，如果忽略其他因素的影响，篮球处于上升阶段的水平距离越长，则被“盖帽”的可能性越大，收集几次篮球比赛的数据之后，某球员投篮可以简化为下述数学模型：如图所示，该球员的投篮出手点为，篮框中心点为，他可以选择让篮球在运行途中经过，，，四个点中的某一点并命中，忽略其他因素的影响，那么被“盖帽”的可能性最大的线路是
A．B．C．D．
第二部分 非选择题
二、填空题（共8小题，满分16分，每小题2分）
9．若分式有意义，则实数的取值范围为 ．
10．分解因式： ．
11．若关于的一元二次方程有实数根，则的取值范围为 ．
12．下列命题中，正确命题的个数为 ．
①所有的正方形都相似
②所有的菱形都相似
③边长相等的两个菱形都相似
④对角线相等的两个矩形都相似
13．如图，四边形是的内接四边形，，弦，则的半径等于 ．
14．甲、乙、丙三名同学观察完某个一次函数的图象，各叙述如下：
甲：函数的图象经过点；
乙：随的增大而减小；
丙：函数的图象不经过第三象限．
根据他们的叙述，写出满足上述性质的一个函数表达式为 ．
15．“共和国勋章”获得者、“杂交水稻之父”袁隆平为世界粮食安全作出了杰出贡献．全球共有40多个国家引种杂交水稻，中国境外种植面积达800万公顷．某村引进了甲、乙两种超级杂交水稻品种，在条件（肥力、日照、通风不同的6块试验田中同时播种并核定亩产，统计结果为：亩，，亩，，则 品种更适合在该村推广．（填“甲”或“乙”
16．为了从2018枚外形相同的金蛋中找出唯一的有奖金蛋，检查员将这些金蛋按的顺序进行标号．第一次先取出编号为单数的金蛋，发现其中没有有奖金蛋，他将剩下的金蛋在原来的位置上又按编了号（即原来的2号变为1号，原来的4号变为2号原来的2018号变为1009号），又从中取出新的编号为单数的金蛋进行检验，仍没有发现有奖金蛋如此下去，检查到最后一枚金蛋才是有奖金蛋，问这枚有奖金蛋最初的编号是 ．
三、解答题（共68分，第17-20题，每题5分，第21-22题，每题6分，第23题5分，第24题6分，第25题5分，第26题6分，第27-28题，每题7分）解答应写出文字说明、演算步骤或证明过程。
17．（5分）计算：．
18．（5分）解不等式组：，在数轴上表示解集并列举出非正整数解．
19．（5分）先化简，再求值：，其中．
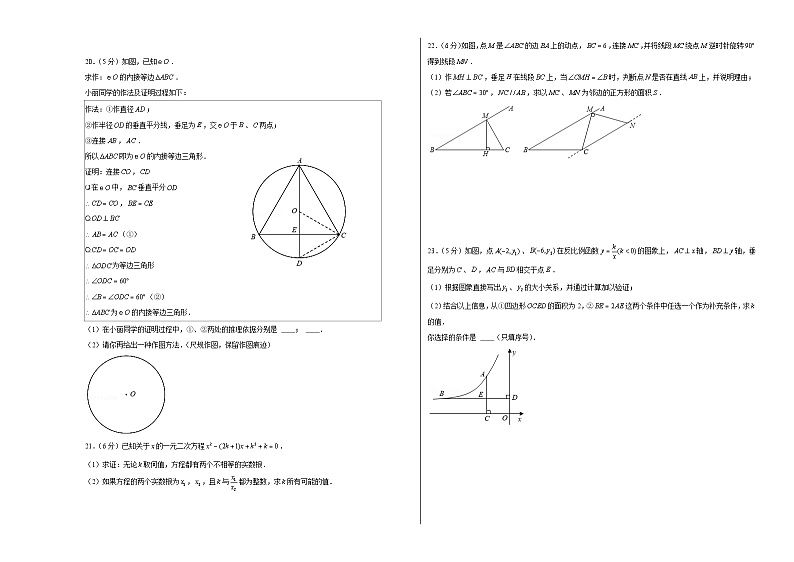
20．（5分）如图，已知．
求作：的内接等边．
小丽同学的作法及证明过程如下：
（1）在小丽同学的证明过程中，①、②两处的推理依据分别是 ； ．
（2）请你再给出一种作图方法．（尺规作图，保留作图痕迹）
21．（6分）已知关于的一元二次方程．
（1）求证：无论取何值，方程都有两个不相等的实数根．
（2）如果方程的两个实数根为，，且与都为整数，求所有可能的值．
22．（6分）如图，点是的边上的动点，，连接，并将线段绕点逆时针旋转得到线段．
（1）作，垂足在线段上，当时，判断点是否在直线上，并说明理由；
（2）若，，求以、为邻边的正方形的面积．
23．（5分）如图，点、在反比例函数的图象上，轴，轴，垂足分别为、，与相交于点．
（1）根据图象直接写出、的大小关系，并通过计算加以验证；
（2）结合以上信息，从①四边形的面积为2，②这两个条件中任选一个作为补充条件，求的值．
你选择的条件是 （只填序号）．
24．（6分）为了防控新冠疫情，某地区积极推广疫苗接种工作，卫生防疫部门对该地区八周以来的相关数据进行收集整理，绘制得到图表：
该地区每周接种疫苗人数统计表
根据统计表中的数据，建立以周次为横坐标，接种人数为纵坐标的平面直角坐标系，并根据以上统计表中的数据描出对应的点，发现从第3周开始这些点大致分布在一条直线附近，现过其中两点、作一条直线（如图所示，该直线的函数表达式为，那么这条直线可近似反映该地区接种人数的变化趋势．
请根据以上信息，解答下列问题：
（1）这八周中每周接种人数的平均数为 万人；该地区的总人口约为 万人；
（2）若从第9周开始，每周的接种人数仍符合上述变化趋势．
①估计第9周的接种人数约为 万人；
②专家表示：疫苗接种率至少达，才能实现全民免疫．那么，从推广疫苗接种工作开始，最早到第几周，该地区可达到实现全民免疫的标准？
（3）实际上，受疫苗供应等客观因素，从第9周开始接种人数将会逐周减少万人，为了尽快提高接种率，一旦周接种人数低于20万人时，卫生防疫部门将会采取措施，使得之后每周的接种能力一直维持在20万人．如果，那么该地区的建议接种人群最早将于第几周全部完成接种？
25．（5分）如图，在中，是直径，弦，垂足为，为上一点，为弦延长线上一点，连接并延长交直径的延长线于点，连接交于点，若．
（1）求证：是的切线；
（2）若的半径为8，，求的长．
26．（6分）在平面直角坐标系中，点和点在抛物线上．
（1）若，，求该抛物线的解析式以及它的对称轴；
（2）若，点，，在该抛物线上．若，比较，，，0的大小，用小于号将他们连接，并说明理由．
27．（7分）在和中，，，且，，将绕点顺时针方向旋转，把点在边上时的位置作为起始位置（此时点和点位于的两侧），设旋转角为，连接，点是线段的中点，连接，．
（1）如图1，当在起始位置时，猜想：与的数量关系和位置关系，并说明理由；
（2）如图2，当时，点落在边上，请判断与的数量关系和位置关系，并证明你的结论；
（3）当时，若，，请直接写出的值．
28．（7分）在平面直角坐标系中，对于点，，给出如下定义：若且，我们称点是线段的“潜点”．
已知点，．
（1）在，，，中是线段的“潜点”是 ；
（2）若点在直线上，且为线段的“潜点”，求点横坐标的取值范围；
（3）直线与轴交于点，与轴交于点，当线段上存在线段的“潜点”时，直接写出的取值范围为 ．
考
生
须
知
本试卷共两部分，28道题。满分100分。考试时间120分钟。
在试卷和草稿纸上准确填写姓名、准考证号、考场号和座位号。
试题一律填涂或书写在答题卡上，在试卷上作答无效。
在答题卡上，选择题、作图题用2B铅笔作答，其他试题用黑色字迹签字笔作答。
考试结束，将本试卷、答题卡和草稿纸一并交回。
作法：①作直径；
②作半径的垂直平分线，垂足为，交于、两点；
③连接，．
所以即为的内接等边三角形．
证明：连接，
在中，垂直平分
，
（①）
为等边三角形
（②）
为的内接等边三角形．
周次
第1周
第2周
第3周
第4周
第5周
第6周
第7周
第8周
接种人数（万人）
7
10
12
18
25
29
37
42